|
одного, в зависимости от знака a и четности n. Корень n-й степени из
нуля имеет только одно значение, равное нулю, т. е. 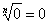
.
Рассмотрим важный частный случай извлечения корня, а именно извлечения корня n-й
степени из числа 1. Представляя это число в тригонометрической форме 1=cos0+
isin0 и применяя формулу (34), получаем n значений корня из единицы:
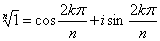 , k = 0, 1, 2, . , n – 1. (35) , k = 0, 1, 2, . , n – 1. (35)
На комплексной плоскости корни n-й степени из единицы изображаются точками,
расположенными на окружности радиуса R = 1 и делящими ее на n равных дуг.
Одной из таких точек будет точка, изображающая число 1.
Например: найдем все значения корня шестой степени из единицы. По формуле
(35), которая в данном случае принимает вид
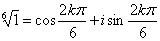 , k = 0, 1, 2, 3, 4, 5, , k = 0, 1, 2, 3, 4, 5,
получаем шесть следующих значений:
 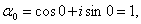
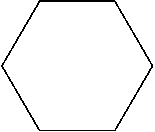 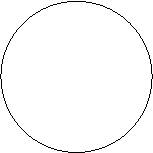 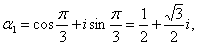

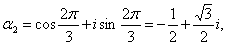
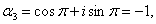
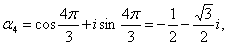
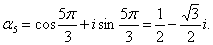
Эти значения изображаются вершинами правильного шестиугольника, вписанного в
единичную окружность (рис. 3).
Где применяются комплексные числа?
В течение последних двухсот лет комплексные числа находят многочисленные, а
иногда и совершенно неожиданные применения. Так, например, с помощью
комплексных чисел Гаусс нашел ответ на чисто геометрический вопрос: при
каких натуральных n циркулем и линейкой можно построить правильный n-
угольник? Из школьного курса геометрии известно, как циркулем и линейкой
построить некоторые правильные многоугольники: правильный треугольник,
квадрат, правильный шестиугольник (его сторона равна радиусу описанной около
него окружности). Более сложным является построение правильных пятиугольника
и пятнадцатиугольника. Научившись строить эти правильные многоугольники,
легко перейти к построению соответствующих многоугольников с удвоенным
числом сторон: восьмиугольника, десятиугольника и т. п. Все эти задачи на
построение были решены еще в Древней Греции. Однако, несмотря на огромные
усилия многих замечательных древнегреческих геометров и других ученых,
никому не удалось построить ни правильный семиугольник, ни правильный
девятиугольник. Не удалось также осуществить построение правильного р-
угольника ни при каком простом числе р, кроме p = 3 и p = 5. Более двух тысяч
лет никто не мог продвинуться в решении этой проблемы. В 1796 г. Карл Фридрих
Гаусс, 19-летний студент-математик Геттингенского университета, впервые
доказал возможность построения правильного семнадцатиугольника с помощью
циркуля и линейки. Это было одно из самых удивительных открытий в истории
математики. В течение нескольких последующих лет Гаусс полностью решил
проблему построения правильных n-угольников.
Гаусс доказал, что правильный N–угольник с нечетным числом сторон (вершин)
может быть построен с помощью циркуля и линейки тогда и только тогда, когда
число N является простым числом Ферма или произведением нескольких различных
простых чисел Ферма. (Числами Ферма называют числа вида Fn = 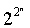
+ 1 · При n = 0, 1, 2, 3, 4 эти числа являются простыми, при n = 5 число F5
будет составным. Из этого результата следовало, что построение правильного
многоугольника невозможно при N = 7, 9, 11, 13.
Легко заметить, что задача о построении правильного n-угольника равносильна
задаче о делении окружности радиуса R = 1 на n равных частей. Выше было
показано, что корень n-й степени из единицы имеет точно n значений; почти все
эти значения (за исключением одного, двух) являются комплексными. Точки,
изображающие корни n-й степени из единицы, располагаются на окружности
радиуса R = 1 и делят ее на n равных дуг, т. е. являются вершинами
правильного n-угольника, вписанного в эту окружность (см. рис. 3). При
доказательстве возможности построения правильного 17-угольника Гаусс
пользовался свойствами корней 17-й степени из единицы.
 
В XVIII в. возникла новая область математики – теория функций комплексной
переменной. Введем понятие такой функции. Рассмотрим две комплексные
переменные z = x + iy и w = u + iv, где x, y, u, v –
действительные переменные, i = 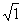
- мнимая единица. Зафиксируем две комплексные плоскости Oxy (плоскость z), O'uv
(плоскость w) с выбранными на них системами прямоугольных координат и два
множества на этих плоскостях: D и D' соответственно (рис. 4).
Если каждой точке z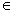 D D
по некоторому закону f ставится в соответствие единственная точка w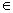
D', то говорят, что w есть функция от z и пишут: w = f(z). Множество D в этом
случае называют областью определения функции w = f(z), значения
которой принадлежат области D'. Если множество значений f(z) исчерпывает все
множество D', то D' называют множеством значений (областью изменения)
функции f(z). B таком случае пишут: D'= f(D). Множества D и D' можно
изображать на одной комплексной плоскости. Каждое из множеств D и D' может
совпадать со всей плоскостью.
Таким образом, каждая комплексная функция реализует однозначное в одну
сторону отображение одного множества на другое. Благодаря этому комплексные
функции находят важные применения таких науках, как гидродинамика и
аэродинамика, поскольку с их помощью удобно описывать движение объема
жидкости (или газа).
С помощью теории функций комплексной переменной доказана следующая важная
теорема, которую долгое время называли основной теоремой алгебры.
Теорема: Всякий многочлен с любыми числовыми коэффициентами,
степень которого не меньше единицы, имеет хотя бы один корень, в общем случае
комплексный.
Рассмотрим многочлен степени n (n ≥ 1):
f(x) = a0xn + a1xn-1 + . + an-1x + an . (36)
Корнем многочлена называют такое число с (в общем случае комплексное: с
= a + bi), которое обращает данный многочлен в нуль:
a0cn + a1cn-1 + . + an-1c + an ≡ 0.
Другими словами, теорема утверждает, что алгебраическое уравнение n-й
степени (n ≥ 1)
a0xn + a1xn-1 + . + a
n-1x + an = 0
37)
имеет хотя бы один корень.
Отсюда следует, что любое алгебраическое уравнение n-й степени имеет ровно n
корней. Действительно, если многочлен f(х) = a0xn + a
1xn-1 + . + an-1x + an
, имеет корень α1, то его можно представить в виде f(х) = (х –
α1)φ1(x), где φ1(x) –
многочлен степени n – 1. Этот многочлен по данной теореме имеет хотя бы один
корень. Обозначим корень многочлена φ1(x) через α2
, тогда φ1(x) = (х – α2)φ2(x),
где φ2(x) – многочлен степени n – 2. Продолжая аналогичные
рассуждения, находим, что f(x) = a0(x – a1)(x – a2
)...(x – an). Отсюда видно, что f(αi) = 0 при i – 1,
2, ... , n, т. е. αi — корни многочлена (36) или уравнения
(37). Таким образом, уравнение (37) имеет n корней.
Отметим, что комплексные корни всякого многочлена с действительными
коэффициентами всегда сопряжены: если с = a - bi – корень уравнения, то
с = а-bi – также корень данного уравнения. Иными словами, комплексные
корни такого многочлена входят парами во множество его корней. Отсюда следует,
что любое алгебраическое уравнение нечетной степени имеет хотя бы один
действительный корень.
Замечание. Не всякое уравнение имеет корни, действительные или
комплексные. Например, трансцендентное (неалгебраическое) уравнение аx
= 0 (а > 0) не имеет никаких корней (ни действительных, ни комплексных).
  
Простейшим примером функции комплексной переменной является линейная функция w =
z + c, где с – постоянная (комплексное число). Эта функция осуществляет
преобразование плоскости z на плоскость w. Каждой точке z она ставит в
соответствие точку w = z + с. Очевидно, от точки z можно перейти к точке w
путем сдвига (параллельного переноса) на вектор с, т. е. посредством
перемещения точки z по направлению вектора с на расстояние, равное
длине этого вектора (рис. 5). Путем подходящего выбора числа с можно получить
любой сдвиг. Например, если точку z нужно сдвинуть в положительном направлении
оси Ox на две единицы, то надо взять с = 2; точка w = z + 2 будет искомой (рис.
6). Если же точку z нужно сдвинуть в отрицательном направлении оси Oy на три
единицы, то берем c = -3i; точка w'= z + (-3i) = z – 3i
будет искомой (рис. 6). Итак, функция w = z + c осуществляет преобразование
(отображение) плоскости, которое называют сдвигом на вектор с.

Геометрическое преобразование, при котором величины углов между любыми двумя
линиями, содержащимися в преобразуемой фигуре, не изменяются, называют
конформным преобразованием или конформным отображением. (Под углом
между двумя линиями, пересекающимися в некоторой точке, понимают угол между
касательными к этим линиям, проведенными в этой точке.) Примерами конформных
отображений могут служить сдвиг (параллельный перенос), гомотетия и поворот.
Таким образом, можно сказать, что функция w = z + с осуществляет конформное
отображение; это одна из таких функций.
Теория функций комплексной переменной находит широкое применение при решении
важных практических задач картографии, электротехники, теплопроводности и
др. Во многих вопросах, где речь идет, например, об электрическом потенциале
в точках пространства, окружающего заряженный конденсатор, или о
температуре внутри нагретого тела, о скоростях частиц жидкости или газа в
потоке, движущемся в некотором канале и обтекающем при этом некоторые
препятствия, и т. п., нужно уметь находить потенциал, температуру, скорости и
т. п. Задачи такого рода могут быть решены без особых затруднений в случае,
когда встречающиеся в них тела имеют простую форму (например, в виде плоских
пластин или круговых цилиндров). Однако расчеты необходимо уметь производить
и во многих других случаях. Например, чтобы сконструировать самолет, надо
уметь вычислять скорости частиц в потоке, обтекающем крыло самолета.
Разумеется, при полете самолета движутся и частицы воздуха, и само крыло.
Однако, опираясь на законы механики, исследование можно свести к случаю,
когда крыло неподвижно, а на него набегает и обтекает его поток воздуха.
Крыло самолета в поперечном
 разрезе, (профиль крыла) имеет разрезе, (профиль крыла) имеет
вид,  показанный на рисунке 7. показанный на рисунке 7.
Расчет скоростей производится достаточно просто, когда поперечный разрез
обтекаемого тела есть круг (т. е. само тело является круглым цилиндром). Чтобы
свести задачу о скоростях частиц потока  
воздуха, обтекающего крыло самолета, к более простой задаче обтекания круглого
цилиндра,  достаточно достаточно
конформно отобразить часть плоскости, заштрихованную на рисунке 7, а (вне
крыла), на другую фигуру, заштрихованную на рисунке 7, б (вне круга). Такое
отображение осуществляется с помощью некоторой функции комплексной
переменной.
Знание этой функции позволяет перейти от скоростей в потоке, обтекающем
круглый
цилиндр, к скоростям в потоке, обтекающем крыло самолета, и тем самым
полностью решить поставленную задачу.
Конформное отображение, заданное соответствующей функцией комплексной
переменной, аналогичным образом позволяет сводить решение задач о расчете
электрического потенциала и температур от случая тел произвольной формы
(любого профиля сечения) к простейшим случаям, для которых задачи решается
легко.
Русский и советский ученый H. E. Жуковский (1847–1921) успешно применял
теорию функций комплексной переменной к решению важных прикладных задач.
Так, методами этой теории он доказал основную теорему о подъемной силе крыла
самолета. В. И. Ленин назвал H. E. Жуковского «отцом русской авиации». В
одном из своих выступлений H. E. Жуковский говорил: «...человек не имеет
крыльев и по отношению веса своего тела к весу мускулов он в 72 раза слабее
птицы; ...он почти и 800 раз тяжелее воздуха, тогда как птица тяжелее воздуха
в 200 раз. Но, я думаю, что он полетит, опираясь не на силу своих мускулов, а
на силу своего разума». (Жуковский H.E. Собрание сочинений. – М. – Л.:
Гостехиздат, 1950. –T. 7. – С. 16.) С помощью теории функций комплексной
переменной H.E. Жуковский решал задачи, относящиеся к вопросам просачивания
воды через плотины.
Страницы: 1, 2, 3, 4, 5, 6
| 


