p>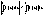 6. Пусть 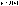 интегрируема на интегрируема на 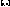 , ,  , то существует М, такая что , то существует М, такая что 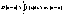 25.Интеграл с переменным верхним пределом. Теорема о его непрерывности. Теорма: Если функция f(x) интегрируема на отрезке [a,b], то функция 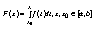
непрерывна на этом отрезке. Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆хÎ[a,b]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек: a x0 x х+∆х b Получим: По теореме (Если функция y=f(x) интегрируема на отрезке, то интегрируема и абсолютная величина |f(x)|, причем .(на этом теорема закончилась, но неравенство относится к ней.) и следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства: (на этом следствие из теоремы закончилось) получаем: Отсюда следует, что при ∆х→0 будет ∆F→0. Это доказывает непрерывность функции F(x). Отметим, что для подынтегральной функции f(x) точка х может быть точкой разрыва. 26.Формула Ньютона-Лейбница. Пусть F(x) -произвольная первообразная для функции f(x), заданной на промежутке [a,b]. Так как две первообразные одной и той же функции отличаются на постоянное слагаемое, то верно равенство (1): 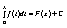
( в качестве числа х0 взято число а). В этом тождестве положим х=а и получим , Откуда С = -F(a). Формула (1) примет вид: Заменяя здесь х на b, приходим к формуле Ньютона-Лейбница: 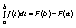
Иногда ее правую часть записывают короче с помощью двойной подстановки: 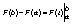
27.Замена переменных в определенном интеграле. Теорема: при замене переменной х на t по формуле x=φ(t) равенство (1) 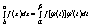
Справедливо при условиях: 1. φ(α) = а, φ(β) = b, 2. φ'(t) непрерывна на отрезке [α,β], 3 f(x) непрерывна на отрезке [a,b], а f[φ(t)] определена непрерывна на отрезке [α,β]. Доказательство: при наших предположениях левая и правая части равенства (1) существуют и существуют первообразные подынтегральные функции. Пусть ∫f(x)dx = F(x)+C. Тогда, как легко проверить дифференцированием обеих частей, справедливо равенство ∫f[φ(t)]φ'(t)dt = F[φ(t)]+C правая часть дифференцируется как сложная функция). Применяем формулу Ньютона-Лейбница Получаем 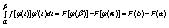
(по условию 1) правые части этих двух равенств оказываются одинаковыми, следовательно, можно приравнять левые части. Приравнивая их, приходим к равенству (1). Ч.т.д. 28.Формула интегрирования по частям определенного интеграла. Пусть u и v - непрерывно дифференцируемые функции. Проинтегрируем равенство d(uv)=udv+vdu в пределах от a до b. В левой части применим формулу Ньютона-Лейбница: Получим: |
29.Приложение определенного интеграла. Площадь криволинейной трапеции. Площадь s криволинейной трапеции, ограниченной кривой у=Ах2+Вх+С, проходящей через точки М1 (-h; y1), M2 (0, y2), M3 (h, y3) (рис. 2) выражается формулой 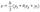 (2) (2)
Доказательство. Подставляя в уравнение у=Ах2+Вх+С координаты точек М1, М2, М3, получаем у1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С, откуда следует, что 2Аh2+2С=у1+у3; С=у2 (3) Учитывая соотношение (3), имеем 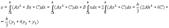
Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x0<x1<x2<...<x2k<x2k+1<x2k+2<...<x2n-1<x2n=b, а кривую y=f(x) с помощью прямых x=xk на 2n соответствующих частей точками М0 , М1 , М2 , ..., М2k , М2k+1 , М2k+2, ..., М2n-2 , М2n-1 , М2n (рис. 3). Через каждую тройку точек М0 М1 М2 , ..., М2k М2k+1 М2k+2, ..., М2n-2 М2n-1 М2n проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x2k, x2k+2], приближенно равна площади соответствующей “параболической” трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)] 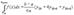
где yk=f(xk), k=0, 1, 2, ...,2n. Складывая почленно эти приближенные равенства, получаем приближенную формулу 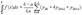
или в развернутом виде 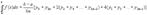
Эта формула называется формулой парабол или формулой Симпсона. 30.Приближенное вычисление определенного интеграла. Формула трапеций. 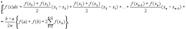
Пусть требуется вычислить интеграл 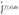 , где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е. , где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е. Где f(xk-1) и f(xk) - соответственно основания трапеций; xk - xk-1 = (b-a)/n - их высоты. Таким образом, получена приближенная формула 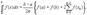
которая и называется формулой трапеций. Эта формула тем точнее, чем больше n. 31.Несобственные интегралы с бесконечными пределами. +++32.Несобственные интегралы второго ряда. Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций. Несобственный интеграл от функции f(x) в пределах от a до +Ґ определяется равенством 
Если этот предел существует, то несобственный интеграл называется сходящимся; если же предел не существует, - расходящимся. Аналогично 
и 
Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a,b] и непрерывна при a <= x < с и с < x < b, то по определению, полагают 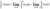
| 33.Числовые ряды. Свойства сходящихся рядов. Рассмотрим числовую последовательность (an)=a1,a2,...,an,. Составим из нее новую последовательность (Sn) следующим образом: S1=а1, S2=a1+a2 S3=a1+a2+a3,, Sn=a1+a2+.+аn=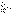 Sn+1=Sn+an+1 Выражение a1+a2+.+аn+an+1+. (1) обозначается символом 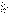 и называется числовым рядом. и называется числовым рядом. Числа а1, а2,.,аn,. называются членами ряда, а число аn- n – м членом или общим членом ряда. Простейшие свойства числовых рядов 1о. Сходимость ряда не нарушится, если произвольным образом изменить (переставить, добавить или отбросить) конечное число членов ряда. 2о. Сходящийся ряд можно почленно умножить на любой множитель  , т.е. если ряд , т.е. если ряд 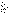 имеет сумму S, то ряд имеет сумму S, то ряд 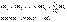
Страницы: 1, 2, 3, 4
|



