|
пространством 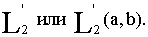
Замечание 1.
В математике называют пространством 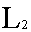
= 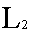 (a (a
, b) совокупность функций ƒ(x), интегрируемых в
лебеговом смысле на [a, b] вместе со своими квадратами,
для которых введено скалярное произведение по формуле (11). Рассматриваемое
пространство 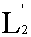 есть часть есть часть 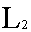
. Пространство 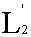 обладает обладает
многими свойствами пространства 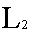
, но не всеми.
Из свойств 1), 2), 3) следует важное неравенство Буняковского |
(ƒ , φ ) | ≤ (ƒ , ƒ )½ (φ , φ )
½, которое на языке интегралов выглядит так:
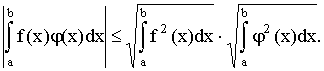
Величина
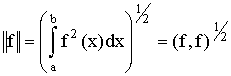
называется нормой функции f.
Норма обладает следующими свойствами:
1) || f
|| ≥ 0, при этом равенство может быть только для нулевой функции
f = 0, т. е. функции, равной нулю, за исключением, быть может,
конечного числа точек;
2) || ƒ + φ ||
≤ || ƒ(x) || || φ ||;
3) || α ƒ || = |
α | · || ƒ ||,
где α – действительное число.
Второе свойство на языке интегралов выглядит так:
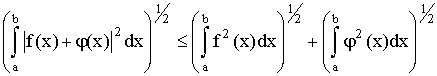
и называется неравенством Минковского.
Говорят, что последовательность функций { f
n }, принадлежит к 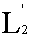
,сходится к функции принадлежит 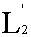
в смысле среднего квадратического на [a, b]
(или ещё по норме 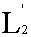 ), если ), если
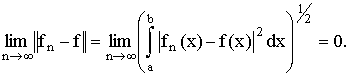
Отметим, что если последовательность функций ƒn
(x) сходится равномерно к функции ƒ(x) на отрезке [a,
b], то для достаточно больших n разность
ƒ(x) - ƒn (x) по абсолютной величине должна
быть мала для всех х из отрезка [a, b].
В случае же, если ƒn (x) стремится к ƒ(x)в
смысле среднего квадратического на отрезке [a, b], то
указанная разность может и не быть малой для больших n
всюду на [a, b]. В отдельных местах отрезка [a,
b] эта разность может быть и велика, но важно только, чтобы интеграл
от её квадрата по отрезку [a, b] был мал для больших
n.
Пример. Пусть на [0, l ] заданна изображенная
на рисунке непрерывная кусочно-линейная функция ƒn
(x) (n = 1, 2,.), причем
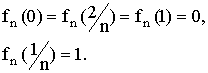
(Бугров, стр. 281, рис. 120)
При любом натуральном n
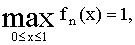
и, следовательно, эта последовательность функций, хотя и сходится к нулю
при n → ∞, но неравномерно. Между тем
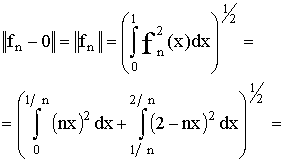
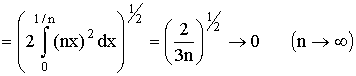
т. е. последовательность функций {fn (х)} стремится к
нулю в смысле среднего квадратического на [0, 1].
Из элементов некоторой последовательности функций ƒ1, ƒ2,
ƒ3,. (принадлежащих 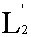 ) )
построим ряд
ƒ1 + ƒ2 + ƒ3 +. (12)
Сумма первых его n членов
σ n = ƒ1 + ƒ2 + . + ƒn
есть функция, принадлежащая к 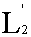
. Если случится, что в 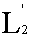
существует функция ƒ такая, что
|| ƒ- σn || → 0 (n → ∞),
то говорят, что ряд (12) сходится к функции ƒ в смысле среднего
квадратического и пишут
ƒ = ƒ1 + ƒ2 + ƒ3 +.
Замечание 2.
Можно рассматривать пространство 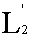
= 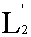 (a, (a,
b) комплекснозначных функций ƒ(x) = ƒ1(x) + i
ƒ2(x), где ƒ1(x) и ƒ2(x) – действительные кусочно – непрерывные
на [a, b] функции. В этом пространстве функции умножаются
на комплексные числа и скалярное произведение функций ƒ(x) = ƒ1(x) +
iƒ2(x) и φ(х) = φ1(х) +i
φ2(х) определяется следующим образом:
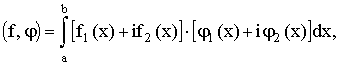
а норма ƒ определяется как величина
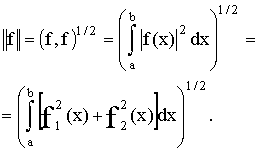
2.1. Интегралы от периодических функций.
Пусть ƒ(x) – периодическая функция, с периодом Т, интегрируемая на
любом сегменте вида [х0, х0+Т]. Тогда величина интеграла 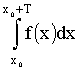
остаётся при любом х0 одной и той же: для любых х0, х0'
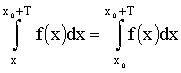 . .
2.2. Интегралы от некоторых тригонометрических  функций. функций.
Укажем значения некоторых интегралов:
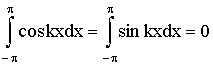 (k = 1,2,.), (13) (k = 1,2,.), (13)
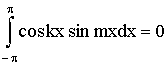 (k =1,2,..; m =1,2,.), (14) (k =1,2,..; m =1,2,.), (14)
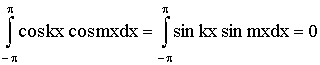 (15) (15)
(k =1,2,.; m =1,2,.; k ≠ m),
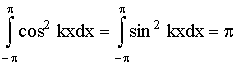 (k =1,2,.) (16) (k =1,2,.) (16)
Теперь можем вычислить коэффициенты Фурье ak и
bk ряда (2). Для разыскания коэффициента an при каком-либо
определенном значении n≠0 умножим обе части
равенства (2) на cosnx и произведя математические операции
в пределах от –π до π, получим:
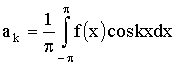 (17) (17)
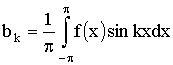 (18) (18)
 Коэффициенты, Коэффициенты,
определенные по формулам (4), (17), (18) называются
коэффициентами Фурье функции ƒ(x), а составленный тригонометрический
ряд (18) с такими коэффициентами называется рядом Фурье функции
ƒ(x).
В некоторых случаях, для более узких классов функций, формулы (17), (18)
были известны ещё Эйлеру. Таким образом, эти формулы ещё называют формулами
Эйлера-Фурье.
Обратим внимание, что постоянная 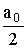
в (2) пишется в таком виде, чтобы придать единообразие формулам (17) и (18).
Вышеприведенные соображения показывают, что поиски тригонометрического
разложения данной функции целесообразно начать с изучения её ряда Фурье,
откладывая на потом строгое изучение вопроса о том, для каких функций ряд
сходится, и притом именно к данной функции. Пока же этого не сделано, функции
ƒ(x) сопоставляют её формальный ряд Фурье, что обычно записывают в виде:
 ƒ(x) ~ ƒ(x) ~ 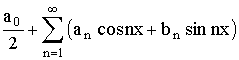 , (19) , (19)
про который известно, что его коэффициенты вычислены по функции ƒ(x)
по формулам Эйлера – Фурье (4), (17) и (18), но ничего не утверждается о его
сходимости и тем более – о его сходимости к данной функции.
Из определения ряда Фурье не следует, что функция должна в него
разлагаться. Из сказанного выше следует только, что некоторая функция допускает
разложение в равномерно сходящийся ряд вида (19), то этот ряд будет её рядом
Фурье.
3. Признаки сходимости  рядов Фурье. (стр. 331, Пискунов) рядов Фурье. (стр. 331, Пискунов)
Зададим вопрос: какими свойствами должна обладать функция, чтобы
построенный, для неё ряд Фурье сходился и чтобы сумма построенного ряда Фурье
равнялась значениям данной функции в соответствующих точках?
Сформулируем теорему, которая даст достаточные условия представимости
функции ƒ(x) рядом Фурье. (из Пискунова)
Определение. Функция ƒ(x) называется кусочно-
монотонной на отрезке [a, b], если этот отрезок можно разбить
конечным числом точек х1, х2, .,хn-1 на интервалы (а,
х1), (х1, х2),., (хn-1, b) так, что на каждом
из интервалов функция монотонна, т. е. либо не возрастающая, либо неубывающая.
Теорема.
Если периодическая функция ƒ(x) с периодом 2π – кусочно
монотонная и ограниченная на отрезке [-π, π], то ряд Фурье,
построенный для этой функции, сходится во всех точках. Сумма полученного ряда
s(x) равна значению функции ƒ(x) в точках непрерывности функции.
В точках разрыва функции ƒ(x) сумма ряда равняется среднему
арифметическому пределов функции ƒ(x) справа и слева, т. е. если х = с –
Страницы: 1, 2, 3, 4, 5, 6
| 


