|
точка разрыва функции ƒ(x), то
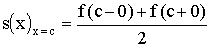 . .
Из этой теоремы следует, что класс функций, представимых рядами Фурье,
довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах
математики. Особенно успешно ряды Фурье применяются в математической физике и
её приложениях к конкретным задачам механики и физики.
Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс
высшей математики», Шнейдер и др., стр. 181)
При выводе формул (4), (17), (18) мы заранее предполагали, что функция
ƒ(x) разлагается в правильно сходящийся тригонометрический ряд (1). Если
же такого предположения не делать, а допустить, что для функции ƒ(x)
существуют все интервалы, стоящие в правых частях формул (4), (17), (18), то по
этим формулам можно вычислить коэффициенты a0, ak и bk и составить
тригонометрический ряд (1), который представляет собой ряд Фурье,
соответствующий данной функции.
Является ли построенный таким образом ряд Фурье сходящимся и если он
сходится, то имеем ли мы право утверждать, что он сходится именно к функции
ƒ(x), с помощью которой вычислялись коэффициенты ряда?
Оказывается, что сходимость ряда Фурье к заданной функции имеет место для
довольно широкого класса функций. Достаточные условия сходимости ряда Фурье, и,
следовательно, возможность разложения функций в ряд Фурье даются теоремой
Дирихле. Прежде чем формулировать эту теорему, введем два определения.
Функция ƒ(x) называется кусочно-монотонной на сегменте [
a, b], если этот сегмент можно разделить на
конечное число сегментов, внутри каждого, из которых функция либо только
возрастает, либо только убывает, либо постоянна.
Основное определение. Функция ƒ(x) называется
удовлетворяющей условиям Дирихле на сегменте [a,
b], если:
1)функция непрерывна на сегменте [a
, b] или же имеет
на нем конечное число точек разрыва 1 рода;
2) функция кусочно-монотонна на сегменте [a, b].
3.1. Примеры разложения функций в ряды Фурье.
Пример 1. Периодическая функция ƒ(x) с периодом 2π определяется
следующим образом: ƒ(x) = х , -π < x ≤ π.
Эта функция – кусочно монотонная и ограниченная. Следовательно, её можно
разложить в ряд Фурье.
По формуле (4) находим:
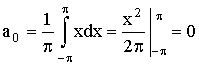
Применяя формулам (17), (18) и интегрируя по частям, получим:
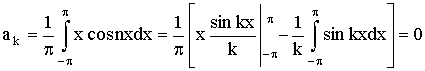
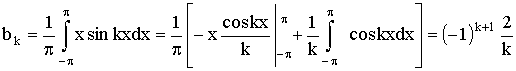
.
Таким образом, получаем ряд:
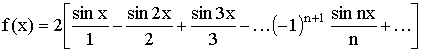
.
Это равенство имеет место во всех точках, кроме точек разрыва. В каждой
точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и
слева, т. е. нулю.
Пример 2. Периодическая функция ƒ(x) с периодом 2π определена
следующим образом:
ƒ(x) = -1 при –π < x < 0,
ƒ(x) = 1 при 0 ≤ x ≤ π.
Эта функция кусочно монотонна и ограничена на отрезке [-π,
π]. Вычислим ее коэффициенты Фурье:
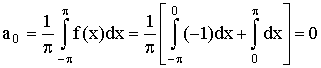 , ,
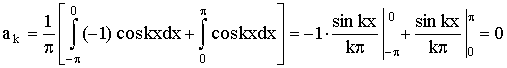
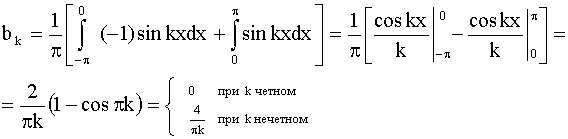
(Нарисовать: рис. 377, стр. 334, Пискунов)
Следовательно, для рассматриваемой функции ряд Фурье имеет вид:
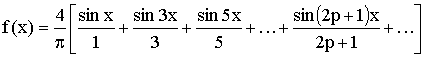
.
Это равенство справедливо во всех точках, кроме точек разрыва.
4. Замечание о разложении периодической функции в ряд Фурье.
Отметим следующее свойство периодической функции ψ(x) с периодом 2π:
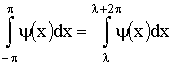 , каково бы ни было число λ. , каково бы ни было число λ.
Действительно, так как ψ(ξ - 2π) = ψ (ξ) , то,
полагая x = ξ - π, можем написать при любых c и d:
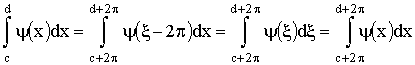
.
В частности, принимая с = - π, d = λ, получим:
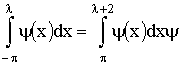
поэтому
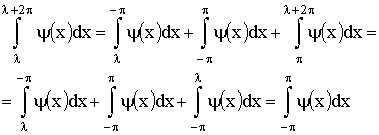
Указанное свойство означает, что интеграл от периодической функции
ψ(x) по любому отрезку, длина которого равна периоду, имеет всегда одно и
тоже значение.
Из доказанного свойства вытекает, что при вычислении коэффициентов Фурье мы
можем заменить промежуток интегрирования (-π, π) промежутком
интегрирования (λ, λ +2π), т. е. можем положить
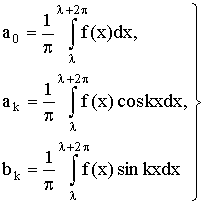  (20) (20)
где λ – любое число.
Это следует из того, что функция ƒ(x) является, по условию,
периодической с периодом 2π; следовательно и функция ƒ(x)·
cоsnx, и ƒ(x)·sinnx являются
периодическими функциями с периодом 2π. В некоторых случаях доказанное
свойство упрощает процесс нахождения коэффициентов.
Пример.
Пусть требуется разложить в ряд Фурье функцию ƒ(x) с периодом 2π,
которая на отрезке 0 < x ≤ 2π задана равенством ƒ(x)= х.
(Пискунов, рис. 382, стр. 339)
Эта функция на отрезке [-π, π] задается двумя формулами:
ƒ(x) = х + 2π на отрезке [-π, 0]
ƒ(x) = х на отрезке [0, π].
В то же время на отрезке [0, 2π] гораздо проще она задается одной
формулой ƒ(x) = х. Поэтому для разложения этой функции в ряд Фурье
выгоднее воспользоваться формулами (20), приравняв λ=0.
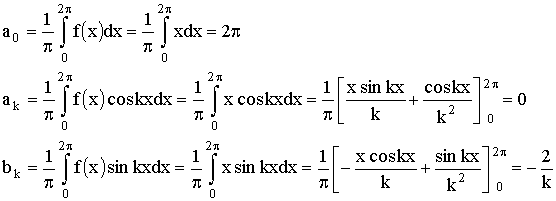
Следовательно,
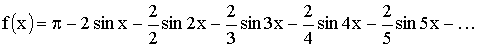
5. Ряды Фурье для чётных и нечётных функций.
Из определения четной и нечетной функции следует, что если ψ(x) –
четная функция, то
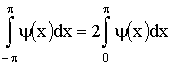 . .
Действительно,
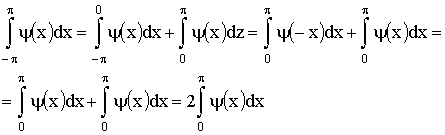
так как по определению четной функции ψ(- x) = ψ(x).
Аналогично можно доказать, что если ψ(x) – нечетная функция, то
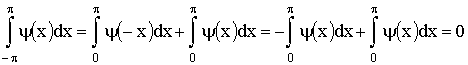
Если в ряд Фурье разлагается нечетная функция ƒ(x), то произведение
ƒ(x) ·coskx есть функция также нечетная, а ƒ(x)
· sinkx – четная; следовательно,
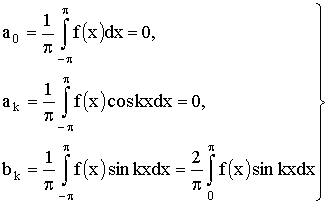 (21) (21)
т. е. ряд Фурье нечетной функции содержит «только синусы».
Если в ряд Фурье разлагается четная функция, то произведение ƒ(x) ·
sinkx есть функция нечетная, а ƒ(x) · coskx
– четная, то:
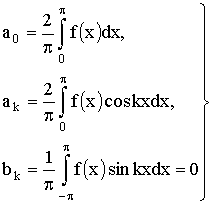 (22) (22)
т. е. ряд Фурье четной функции содержит «только косинусы».
Полученные формулы позволяют упрощать вычисления при разыскании
коэффициентов Фурье в тех случаях, когда заданная функция является четной или
нечетной. Очевидно, что не всякая периодическая функция является четной или
нечетной.
6. Ряд Фурье для функции с периодом 2l.
Пусть функция ƒ(x) есть периодическая функция с периодом 2
l, вообще говоря, отличным от 2π. Разложим её в
ряд Фурье.
Сделаем замену переменной по формуле
 х = lt / π. х = lt / π.
Тогда функция ƒ(lt / π) будет
периодичной функцией от t с периодом 2π. Её
можно разложить в ряд Фурье на отрезке –π ≤ x ≤ π:
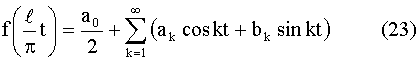
где (Пискунов, стр. 341 – дописывать не надо)
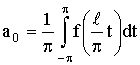
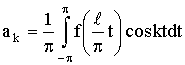
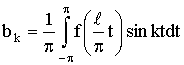
Возвратимся к старой переменной x:
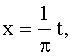 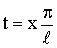 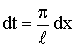
Тогда будем иметь:
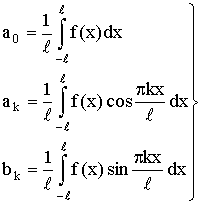 (24) (24)
Формула (23) получит вид
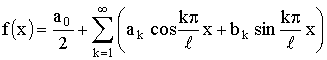 , (25) , (25)
где коэффициенты a0, ak, bk вычисляются по формулам (24). Это и
есть ряд Фурье для периодической функции с периодом 2
l.
Заметим, что все теоремы, которые имели место для рядов Фурье от
периодических функций с периодом 2π, сохраняются и для рядов Фурье от
периодических функций с каким-либо другим периодом 2 l
.
Пример.
Разложить в ряд Фурье функцию ƒ(x) с периодом 2
l, которая на отрезке [-l
, l] задается равенством ƒ(x) = | x |.
(Пискунов, стр.342, рис. 383)
Решение. Так как рассматриваемая функция – четная, то
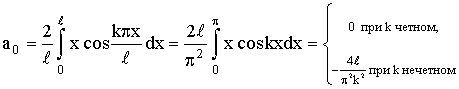
Следовательно, разложение имеет вид

7. Разложение в ряд Фурье непериодической функции.
Пусть на некотором отрезке [a, b
] задана кусочно монотонная функция ƒ(x). Покажем, что данную функцию
Страницы: 1, 2, 3, 4, 5, 6
| 


