|
ƒ(x) в точках её непрерывности можно представить в виде суммы ряда Фурье.
Для этого рассмотрим произвольную периодическую кусочно монотонную функцию
ƒ1(x) с периодом 2μ ≥ a - b, совпадающую с функцией ƒ(x)
на отрезке [a, b]. Таким образом,
дополнили определение функции ƒ(x).
Разложим функцию ƒ1(x) в ряд Фурье. Сумма этого ряда во всех точках
отрезка [a, b] (кроме точек
разрыва) совпадает с заданной функцией ƒ(x), т. е. мы разложили функцию
ƒ(x) в ряд Фурье на отрезке [a, b
].
Рассмотрим следующий важный случай. Пусть функция ƒ(x) задана на
отрезке [0, l]. Дополняя определение этой функции
произвольным образом на отрезке [ l, 0 ] , мы
можем разложить эту функцию в ряд Фурье. В частности, если мы дополним
определение данной функции так, чтобы при - l
≤ х < 0 было ƒ(x) = ƒ(-x). В результате получится четная
функция. В этом случае говорят, что функция ƒ(x) «продолжена четным
образом». Эту функцию разлагают в ряд Фурье, которая содержит только косинусы.
Таким образом, заданную на отрезке [0, l] функцию
ƒ(x) мы разложили по косинусам.
Если мы продолжим определение функции ƒ(x) при - l
≤ х <0 так: ƒ(x) = -ƒ(-x), то получим нечетную функцию,
которая разлагается по синусам. Таким образом, если на отрезке [0,
l] задана некоторая кусочно монотонная функция ƒ(x), то её
можно разложить в ряд Фурье как по косинусам, таки по синусам.
Комплексная форма ряда Фурье для функций с периодом 2π.
Пусть ƒ(x) – функция, удовлетворяющая условиям определения:
Пусть функция ƒ(x) с периодом 2π, имеющая на сегменте [-π,
π] не более конечного числа точек разрыва и абсолютно интегрируема на этом
сегменте (т. е. она интегрируема на любом сегменте).
Тогда пусть ряд (2) является рядом Фурье функции ƒ(x). Преобразуем
общий член этого ряда с помощью формул Эйлера, выражающих косинус и синус через
показательную функцию. Имеем:
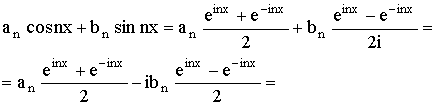
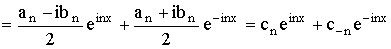 , ,
где 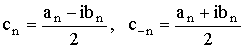 . .
Полагая ещё 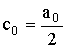 получим для частичных сумм ряда Фурье выражение получим для частичных сумм ряда Фурье выражение
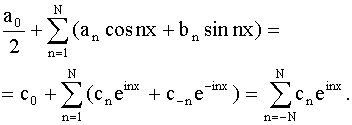
Для новых коэффициентов cn получаем формулу (учитывая формулы an и bn).
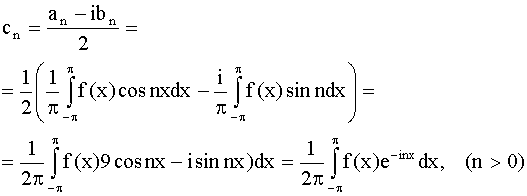
Непосредственно видно, что эта формула верна для n =
0 и для n < 0 (последнее видно,
например, из того, что 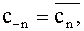 где где 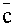
обозначает число, сопряженное с).
По доказанному имеем в точках дифферуемциемоcти:
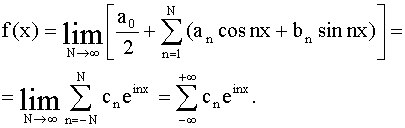
Итак, в точках дифференцируемости
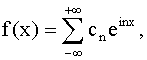 (26) (26)
где
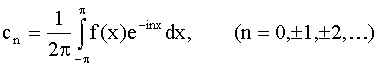
Правая часть формулы (26) представляет собой комплексную форму ряда
Фурье для функции с периодом 2π.
Комплексная форма ряда Фурье для функции с любым периодом. (Романовский стр.33)
Пусть ƒ(x) – функция с периодом 2l,
удовлетворяющая условиям , указанным в пункте 6. Тогда подстановка
x= lt/ π приводит нас к функции ƒ(l
t/ π) с периодом 2π. В силу предыдущего пункта в точках
дифференцируемости имеем:
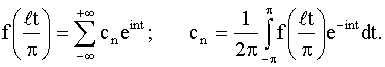
Переходя как в ряде, так и формулах для коэффициентов к старому переменному
х и замечая, что t = π x / l
, dt=(π / l)dx, получим
в точках дифференцируемости:
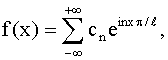 (27) (27)
где
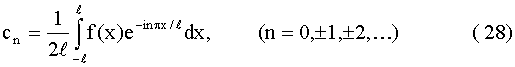
Правая часть формулы (27), где коэффициенты определяются равенствами (28),
называется комплексной формой ряда Фурье для функции с периодом 2
l.
Основные типы уравнений математической физики.
Основными уравнениями математической физики называют (для случая функций
двух независимых переменных) следующие дифференциальные уравнения с частными
производными второго порядка.
1. Волновое уравнение:
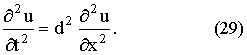
К исследованию этого уравнения приводит рассмотрение процессов поперечных
колебаний струны, продольных колебаний стержня, электрических колебаний в
проводе, крутильных колебаний вала, колебаний газа и т. д. Это уравнение
является простейшим уравнением гиперболического типа.
2.
Уравнение теплопроводности или уравнение Фурье:

К исследованию этого уравнения приводит рассмотрение процессов
распространения тепла, фильтрации жидкости и газа в пористой среде (например,
фильтрации нефти и газа с подземных песчаниках), некоторые вопросы теории
вероятностей и т. д. Это уравнение является простейшим уравнением
параболического типа.
3. Уравнение Лапласа:
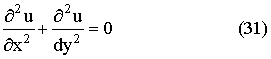
К исследованию этого уравнения приводит рассмотрение задач об электрических
и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики,
диффузии и т. д. Это уравнение является простейшим уравнением
эллиптического типа.
В уравнениях (29), (30) и (31)
искомая функция u зависит от двух переменных.
Рассматриваются также соответствующие уравнения и для функций с большим числом
переменных. Так, волновое уравнение с тремя независимыми переменными имеет
вид:
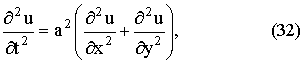
уравнение теплопроводности с тремя независимыми переменными имеет вид:
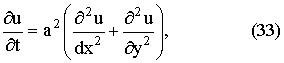
уравнение Лапласа с тремя неизвестными переменными имеет вид:
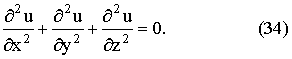
Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод
уравнений электрических колебаний в проводах.
В математической физике под струной понимают гибкую, упругую нить.
Напряжения, возникающие в струне в любой момент времени, направлены по
касательной к её профилю. Пусть струна длины l в
начальный момент напрвлена по отрезку оси Ох от 0 до
l. Предположим, что концы струны закреплены в точках х
= 0 и х = l. Если струну отклонить от
её первоначального положения, а потом предоставить самой себе или, не отклоняя
струны, предать в начальный момент её точкам некоторую скорость, или отклонить
струну и придать её точкам некоторую скорость, то точки струны будут совершать
движения – говорят, что струны начнет колебаться. Задача заключается в
определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения.
В силу этого можно предполагать, что движение точек струны происходит
перпендикулярно оси Ох и в одной плоскости. При этом предположении процесс
колебания струны описывается одной функцией u (x, t), которая дает
величину перемещения точки струны с абсциссой х в момент времени t.
(Н.С. Пискунов стр. 245, рис. 371)
Так как мы рассматриваем малые отклонения струны в плоскости (x,
u ), то будем предполагать, что длина элемента струны М1М2
равняется её проекции на ось Ох, т. е. М1М2 = х2 – х1. Также будем
предполагать, что натяжение во всех точках струны одинаковое; обозначим его
через Т.
Рассмотрим элемент струны ММ′. На концах этого элемента, по
касательным к струне, действуют силы Т.
(Н.С. Пискунов стр. 246, рис. 372)
Пусть касательные образуют с осью Ох углы φ и φ + ∆φ.
Тогда проекция на ось Ou сил, действующих на элемент
ММ′, будет равна T· sin (
φ + ∆φ) – sin φ . Так как угол φ
мал, то можно положить tg φ ≈ sin
φ, мы будем иметь:
T sin (φ + ∆φ) – T sin
φ ≈ T tg (φ + ∆φ) –
T tg φ =
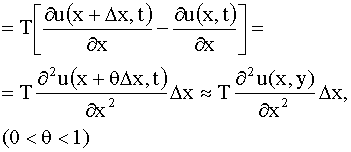
(здесь мы применили теорему Лагранжа к выражению, стоящего в квадратных
скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к
элементу, приравнять силе инерции. Пусть ρ – линейная плотность струны.
Тогда масса элемента струны будет ρ ∆х. Ускорение элемента равно
∂2u / ∂t2.
Следовательно, по принципу Даламбера будем иметь:
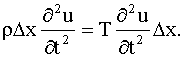
Сокращая на ∆х и обозначая a2 = T/ ρ, получаем уравнение движения

Это и есть волновое уравнение – уравнение колебаний струны. Для
полного определения движения струны одного уравнения (35)
недостаточно. Искомая функция u(x, t) должна удовлетворять ещё
граничным условиям, указывающих, что делается на концах струны (х
= 0 и х = ℓ), и начальным условиям, описывающим состояние струны
в начальный момент (t = 0). Совокупность граничных и начальных
условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при х = 0 и х =
ℓ неподвижны. Тогда при любом t должны выполняться
равенства:
u (0, t) = 0, (36)
u (ℓ, t) = 0. (36,)
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную
форму, которую мы ей придали. Пусть эта форма определяется функцией ƒ(x).
Таким образом, должно быть
u (x, 0) = u |t = 0 = ƒ(x). (37)
Далее в начальный момент должна быть задана скорость в каждой точке струны,
которая определяется функцией φ(х):
Страницы: 1, 2, 3, 4, 5, 6
| 


