Условия (101,) и (101, ,) являются начальными условиями.

Замечание. В частности, может быть, ƒ(x) ≡ 0

или φ(x) ≡ 0. Если же ƒ(x) ≡ 0 и φ(x) ≡ 0,

то струна будет находиться в покое, следовательно, u (x, t)

≡ 0.

Как указывалось выше, к уравнению (30) приводит и задача об электрических

колебаниях в проводах. Покажем это. Электрический ток в проводе характеризуется

величиной ί(x, t) и напряжением υ(x, t),

которые зависят от координаты х точки провода и от времени t.

Рассматривая элемент провода ∆х, можем написать, что падение напряжения на

элементе ∆х равно

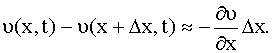
Это падение напряжения складывается из омического, равного ί

R∆x, и индуктивного , равного (∂

ί /∂ t )L∆

x. Итак,

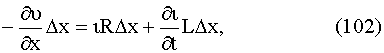
где R и L - сопротивление и

коэффициент самоиндукции, рассчитанный на единицу длины провода. Знак минус

взят потому, что ток течет в направлении, обратном возрастанию

υ. Сокращая на ∆х, получаем уравнение

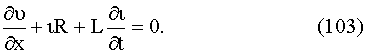
Далее, разность токов, выходящих из элемента ∆х и выходящего из него

время ∆t, будет

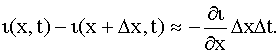
Она расходуется на зарядку элемента, равную C∆

x (∂υ /∂

t) ∆t, и на утечку через боковую

поверхность провода вследствие несовершенства изоляции, равную А

υ∆х∆t (здесь А – коэффициент

утечки). Приравнивая эти выражения и сокращая на ∆x

∆t, получим уравнение:

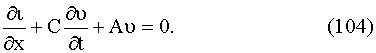
Уравнения (103) и (104) принято называть телеграфными уравнениями.

Из системы уравнений (103) и (104) можно получить уравнение, содержащую

только искомую функцию ί(x, t), и уравнение, содержащее только

искомую функцию υ (x, t). Продифференцируем члены уравнения

(104) по х; члены уравнения (103) продифференцируем по t

и умножим их на С. Произведя вычитание, получим:

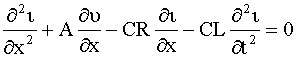
Подставляя в последнее уравнение выражение (∂υ

/∂х) из уравнения (103), получим:

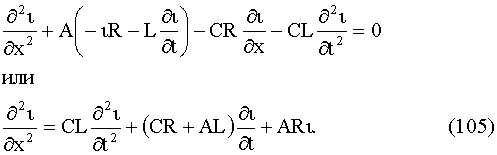
Аналогичным образом получается уравнение для определения υ(x, t):

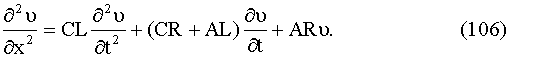
Если можно пренебречь утечкой через изоляцию (А = 0) и сопротивлением (

R = 0), то уравнения (105) и (106) переходят в волновые уравнения:

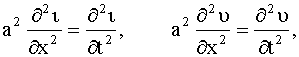
где обозначено: a2 = 1/CL. Исходя из физических

условий, формулируются граничные и начальные условия задачи.

Решение уравнения колебаний струны методом разделения переменных

(методом Фурье).

Метод разделения переменных (или метод Фурье) является типичным для решения

многих задач математической физики. Пусть требуется найти решение уравнения

удовлетворяющее краевым условиям:

u (0, t) = 0, (108)

u (ℓ, t) = 0, (109)

u (x, 0) = ƒ(x), (110)

Будем искать (не равное тождественно нулю) частное решения уравнения (107),

удовлетворяющее граничным условиям (108) и (109), в виде произведения двух

функций X(x) и T(t), из которых

первая зависит только от х, вторая только от t:

u (x, t) = X (x) T (t). (112)

Подставляя в уравнение (107), получаем:

X (x) T′′(t) = a2 X′′(x) T(t).

Разделив члены равенства на a2 XT

В левой части этого равенства стоит функция, которая не зависит от х, слева

– функция, не зависящая от t. Равенство (113) возможно

только в том случае, когда левая и правая части не зависят ни от х, ни от

t, т. е. равны постоянному числу. Обозначим его через – λ, где

λ > 0 ( позднее будет рассмотрен случай λ

< 0). Итак,

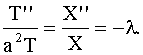
Из этих равенств получаем два уравнения:

X′′ + λX = 0, (114)

T′′ + a2 λT = 0. (115)

Общие решения этих уравнений будут:

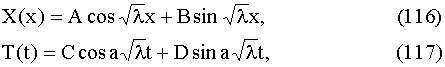
где A, B, C, D – произвольные постоянные.

Подставляя выражения X(x) и T(t) в равенство (112), получим:

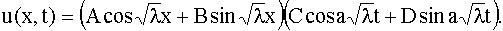
Подберем теперь постоянные А и В так, чтобы удовлетворялись условия (108) и

(109). Так как T (t) тождественно неравна нулю (в

противном случае u (x, t) ≡ 0, что противоречит

поставленному условию),то функция X (x) должна

удовлетворять условиям (108)

и (109), т. е. должно быть Х (0) =0, Х (ℓ) = 0. Подставляя значения

х=0 и х = ℓ в равенство (116), на основании (108) и (109) получаем:

0 = А · 1 + В · 0,

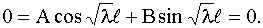
Из первого уравнения находим А = 0. Из второго следует:

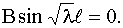
В ≠ 0, так как в противном случае было бы Х ≡ 0 и u

≡ 0, что противоречит условию. Следовательно, должно быть

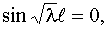
откуда

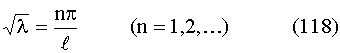
(мы не берем значение n = 0, так как в этом случае

было бы Х ≡ 0 и u ≡ 0). Итак, мы получили:

Найденные значения λ называются собственными значениями для

данной краевой задачи. Соответствующие им функции Х (х) называются

собственными функциями.

Замечание. Если бы мы знали вместо – λ выражение +

λ = k2, то уравнение (114) приняло бы вид

Х′′- k2Х = 0.

Общее решение этого уравнения:

Х = Аekx + Be -kx .

Отличное от нуля решение в такой форме не может удовлетворять граничным

условиям (108) и (109).

Зная λ1/2, мы пользуясь равенством (117) , можем написать:

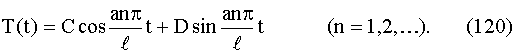
Для каждого значения n, следовательно, для каждого

λ, выражения (119) и (120) подставляем в равенство (112)и получаем

решение уравнения (107), удовлетворяющее граничным условиям (108) и (109). Это

решение обозначим un (x, t):

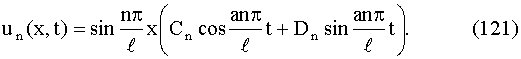
Для каждого значения n мы можем брать свои постоянные

C и D и потому пишем Cn и

Dn (постоянная В включена в Cn и Dn

). Так как уравнение (107) линейное и однородное, то сумма решений также

является решением, и потому функция, представленная рядом

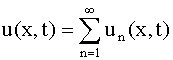
или

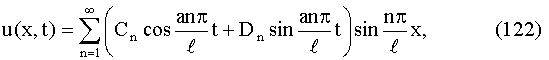
также будет решением дифференциального уравнения (107), которое будет

удовлетворять граничным условиям (108) и (109). Очевидно, ряд (122) будет

решением уравнения (107) только в том случае, если коэффициенты Cn

и Dn таковы, что этот ряд сходится в ряды получающиеся

после двукратного почленного дифференцирования по х и по t

.

Решение (122) должно еще удовлетворять начальным условиям (110) и (111).

Этого мы будем добиваться путем подбора постоянных Cn и

Dn. Подставляя в равенство (122) t

= 0, получим :

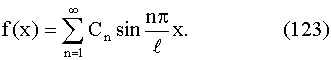
Если функция ƒ(x) такова, что в интервале (0, ℓ) ее можно

разложить в ряд Фурье, то условие (123) будет выполняться, если положить

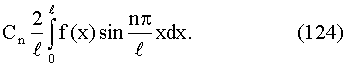
Далее, дифференцируем члены равенства (122) по t и

подставляем t = 0. Из условия (111) получается равенство

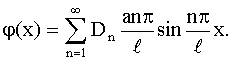
Определяем коэффициенты Фурье этого ряда:

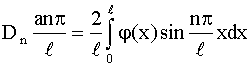
или

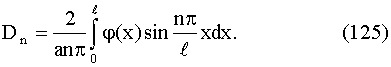
Итак, мы доказали, что ряд (122), где коэффициенты Cn

и Dn определены по формулам (124) и (125), если он

допускает двукратное почленное дифференцирование, представляет функцию

u (x, t), которая является решением уравнения (107) и удовлетворяет

граничным и начальным условиям (108) – (111).

Замечание. Решая рассмотренную задачу для волнового

уравнения другим методом, можно доказать, что ряд (122) представляет собой

решение и в том случае, когда он не допускает почленного дифференцирования. При

этом функция ƒ(x) должна быть дважды дифференцируемой, а функция φ(x)

– один раз дифференцируемой.

Уравнение распространения тепла в стержне. Формулировка краевой задачи.

Рассмотрим однородный стержень длины ℓ. Будем предполагать, что

боковая поверхность стержня теплонепроницаема и что во всех точках поперечного

сечения стержня температура одинакова. Изучим процесс распространения тепла в

стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х =

, а другой – с точкой х = ℓ.

Пискунов стр 252, рис. 373

Страницы: 1, 2, 3, 4, 5, 6