в пределах от 0 до R.

Таким образом, для задачи оптимального управления текущими запасами построена

следующая математическая модель:

при ограничениях 0 < q £ Q (17)

определить значения q, обращающее в минимум нелинейную целевую функцию

Формализованная задача строго математически записывается в виде:

Решение задачи проведем по известной схеме. Вычисляем производную:

И приравниваем её к нулю:

Чтобы убедиться, что в точке q = q0 функция Q(q) действительно достигает

своего минимума, вычислим вторую производную:

Итак, оптимальный размер одной поставки равен:

оптимальный средний текущий запас:

оптимальное число поставок:

оптимальный интервал между двумя последовательными поставками:

оптимальные (теоретические) издержки составят:

ПРИМЕР 1. Торговое предприятие в течение года планирует завести и

реализовать сахар общим объёмом 10 тысяч тон. Стоимость завоза одной партии

товара равна 1000 рублей, а хранение одной тонны сахара обходится в 50 рублей.

Определить оптимальный размер одной поставки, чтобы суммарные расходы по завозу

и хранению товара были минимальны, а также количество поставок, интервал

времени между двумя последовательными поставками и минимальные (теоретические)

суммарные издержки.

По условию задачи: R = 10000, Cs = 1000, C1 = 50, T = 12 мес.

По формулам (19), (21), (22) и (23) имеем:

Итак, оптимальный размер одной поставки равен 632 тонны, количество поставок

nо равно 16, время tso между двумя последовательными поставками равно 23 дня,

а минимальные суммарные расходы составят 31600 рублей.

Заметим, что условия рассмотренной задачи во многом являются

идеализированными. На практике не всегда является возможным придерживаться

полученных теоретических параметров модели управления запасами. Например, в

рассмотренной задаче мы получили, что оптимальный размер одной поставки равен

632 тонны, но может так оказаться, что завод-изготовитель отпускает сахар

только вагонами по 60 тонн. Значит, торговое предприятие вынуждено

отклоняться от оптимального размера одной поставки. Поэтому важно определить

такие пределы отклонения, которые не приводят к существенному возрастанию

суммарных издержек.

Целевая функция Q(q) управления запасами является суммой двух функций –

линейной и гиперболической. Изобразим её график схематически.

В области минимума она изменяется медленно, но с удалением от точки qo, особенно

в сторону малых q, величина Q быстро возрастает. Определим доступные изменения

размера одной поставки по доступному уровню возрастания издержек. Пусть

торговое предприятие “согласно” на возрастание минимальных издержек в не более,

чем b раз (b > 1), т.е. предприятие допускает издержки

Q = bQo (24)

Отклонение размера одной поставки q от оптимального зададим с помощью

дополнительного параметра a в виде:

q = aqo.

Тогда суммарные издержки при таком размере одной поставки будет равны:

из (24) и (25) следует:

Разрешая (26) относительно a получаем:

Пусть в примере 1 предприятие допускает увеличение суммарных издержек на 20% по

сравнению с оптимальными, т.е. b = 1,2. Тогда по формулам (27) получаем: a1 =

1,2 - Ö1,44 - 1 = 0,54; a2 = 1,2 + Ö1,44 - 1 = 1,86. И интервал

допустимых величин a есть 0,54 £ a £ 1,86. Тогда: a1qo =

0,54 * 632 » 341; a2qo = 1,86 * 632 » 1176 и объём одной постановки q может

изменяться в интервале (a1qo; a2q0) = (341; 1176). При этом суммарные издержки

не превысят оптимальные более чем в 1, 2 раза.

Заметим здесь, что полученный допустимый интервал значений q не симметричен

относительно qо, поскольку в сторону уменьшения значений q можно отклониться

от qo на 632 – 341 = 291 единиц, а в сторону увеличения значений q можно

отклоняться от q0 на 1176 – 632 = 544 единиц.

Такая асимметричность допустимых значений q относительно q0 легко объясняется

из графика функции Q на рис.1: при отклонении влево от q0 график функции

возрастает “быстрее”, чем при отклонении на такую же величину вправо от q0.

Рассмотренная выше модель конечно же достаточно проста и может применяться

только на предприятиях реализующих один тип товара, что встречается крайне

редко. Обычно у любого торгового предприятия имеются запасы самых различных

товаров. Если при этом товар не является взаимозаменяемыми, то определение

оптимальных размеров запасов производится отдельно по каждому товару, как это

было показано выше. Взаимозаменяемые товары целесообразно объединить в группы

и для них производить оптимизацию товарных запасов как для отдельных товаров.

На практике, однако, не всегда можно воспользоваться такими рекомендациями,

поскольку могут возникнуть другие ограничительные условия, в частности

ограниченность размеров складских помещений. Такие ограничительные условия

приводят к тому, что оптимальная по величине партия товара не может быть

размещена в имеющийся складской емкости. Рассматриваемая далее модель

учитывает такие ограничения.

7. Модель II. Модель Уилсона с ограничениями на складские помещения

Пусть торговое предприятие в течении периода времени Т должно завести и

реализовать n видов товара. Соответственно обозначим:

Ri - полный спрос i – го товара за время Т;

C1i – стоимость хранения одной единицы i-го товара планируемом периоде времени;

CSi - расходы по завозу одной партии i – го товара;

Vi - объем складского помещения занимаемый одной единицей i –го товара.

V - вся ёмкость складского помещения.

Все эти значения считаются заранее известными. Неизвестный пока размер одной

поставки i-го товара обозначим через qi, а через qio будем в дальнейшем

обозначать оптимальный размер одной поставки i-го товара.

Тогда в соответствии с (2) полные издержки по завозу и хранению i-го товара

будут равны:

а суммарные издержки по всем видам товара принимают вид:

Далее Vi * qi – объем складских помещений, которые занимают i-ый вид товара,

åVi qi - объем складских помещений, занимаемых всеми видами товара и

должно выполняться очевидные соотношения,

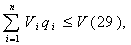
qi £ Ri, qi ³ 0 (30).

Итак, приходим к следующей задаче Лагранжа:

Найти минимум нелинейной функции (12) при линейных ограничениях (29) и (30).

Функция Лагранжа рассматриваемой задачи (28) – (30) имеет вид:

Функция Лагранжа (31) совпадает с целевой функцией (28) в случаи если в (31)

или

Следуя алгоритму решения задачи Лагранжа, найдем частные производные функции

(31) по всем qi и прировняем их к нулю:

Каждое из уравнений системы (34) определяет соответствующее значение

где в правой части все значения параметров известны за исключением множителя

l. Для определения значения подставим выражения qi в условие (32). Получаем:

Страницы: 1, 2, 3, 4, 5