|
В соотношении (36) все величины, кроме l, заранее известны, т.е. оно является
иррациональным уравнением с одним неизвестным. Его всегда можно разрешить
относительно множителя l. Найдя значения l = l0, можно определить оптимальные
величины поставок каждого из товаров по формулам:
Теперь можно рассматривать конкретный пример.
Пусть торговое предприятие намерено завести и реализовать товар трех видов (n
= 3) объемами соответственно 24 тыс. ед, 20 тыс. ед. и 16 тыс. ед. Весь объем
складских помещений составляет 18 000 куб. м. Стоимость хранения одной
единицы первого вида товара 6 руб., второго – 8 руб., третьего – 10 руб.
Расходы по завозу одной партии первого вида товара 1200 руб., второго – 1600
руб., третьего – 2000 руб. При этом одна единица первого вида товара занимает
3 куб. м., второго – 4 куб. м., третьего – 5 куб. м. Найти оптимальные
размеры поставок каждого из видов товара. По условию имеем:
R1 = 24000, R2 = 20000, R3 = 16000;
C11 = 6, C12 = 8, C13 = 10;
Cs1 = 1200, Cs2 = 1600, Cs3 = 2000;
V1 = 3, V2 = 4, V3 = 5;
V = 18000;
Составляем уравнение вида (36) для определения значения множителя l;
или
откуда lо = - 2,41.
Найдем величины оптимальных поставок каждого из товаров по формулам (37):
Проверим выполнимость условия (29) при найденных объемах оптимальных
поставок. Должно выполняться:
V1 * q1о + V2 * q2о + V3 * q3о £ V = 18000.
Имеем:
3 * 1677 + 4 * 1531 + 5 * 1369 = 5031 + 6124 + 6845 = 18000.
Выполнимость неравенства (29) служит подтверждением того, что объемы
оптимальных поставок определены верно. Более того. Неравенство (29) в нашем
примере выполнилось как равенство, что говорит о том, что при первом завозе
товара все складские помещения будут заполнены максимально полно. С течением
времени, при последующих завозах товара, картина будет конечно же не столь
идеальной и какая та часть складских помещений будет не заполнена.
Здесь можем заметить одну небольшую “уловку” в этом примере исходные данные в
примере подобраны так, что иррациональное уравнение (*) вида (36) имеет во
всех трех слагаемых один и тот же знаменатель, что конечно же упрощает
решение уравнения. Эта “уловка” использована для облегчения рассмотрения
примера, поскольку нашей главной целью в настоящий момент не является
возможность разрешения иррационального уравнения. И тем не менее, возникает
вопрос: а что же делать, когда при использовании этой модели на практике
исходные данные будут таковы, что нашей “уловкой” воспользоваться будет
невозможно. Ответ на этот вопрос достаточно прост: в современной математике
разработаны десятки методов приближенных решений уравнений и потому значения
множителя l можно определить из уравнения (36) приближенно с любой степенью
точности. К тому же несмотря на нашу “уловку” облегчающую нахождения значения
l, тем не менее мы определили его приближение. С учетом выше сказанного,
можем прийти к выводу, что использованная “уловка” не сужается общностью
рассмотрения модели.
8. Рацион Робинзона
Обратимся теперь к задаче о потреблении примерно в таком виде, в каком ее
ставил Госсен.
Человек может потреблять блага n видов в количествах хi, i = 1, ., n. Общая
полезность потребления i-того блага описывается функцией TUi(xi). Предельная
полезность MUi(хi) = dTUi(хi)/dxi убывает с ростом хi - в этом состоит закон
Госсена. Полезность потребления всех: благ суммируется по отдельным благам,
так что
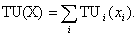
Будем считать, опять-таки следуя Госсену, что потребительские возможности
человека ограничены лишь временем, которое он может затачивать на добывание и
потребление благ, как это имело место у Робинзона Крузо. Если на единицу i-
того блага ему приходится тратить ti единиц времени, то ресурсное ограничение
выражается равенством
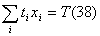
где Т — фонд времени, выделяемый на потребление благ.
Задача рационального потребления теперь сводится к определению такого
“рациона” - набора благ Х = (х1,.,хn), - который доставляет максимум TU(X)
при ограничении (38).
Лагранжиан этой задачи:
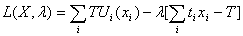 . .
Условия оптимума выражается системой
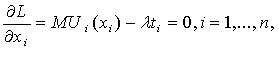
или
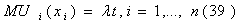
Итак, предельные полезности различных благ в точке оптимума пропорциональны
удельным затратам времени. Это значит, что для любой пары благ (i, j)
отношение их предельных полезностей равно отношению удельных затрат времени:
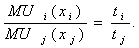
А отсюда следует, что дополнительная малая порция времени (скажем, минута),
затрачиваемая на любое из благ, дает один и тот же прирост полезности.
Величина этого прироста, определяется коэффициентом l: если Робинзон сможет
выделить на потребление благ дополнительно ÙТ единиц времени, то общая
полезность возрастет при этом на величину
ÙTU » lÙT. (40)
Заметим, что убывание предельной полезности гарантирует единственность
оптимума. Если взять другие значения хi, (обозначим их хi'), также
удовлетворяющие условиям, пропорциональности предельных полезностей удельным
затратам времени:
MUi(xi') = li' ti
то либо l’ > l, тогда xi' < xi. для всех продуктов (предельная полезность
убывает с ростом xi); либо l’ < l - для всех i. В первом случаи потребное
количество времени меньше Т, во втором – больше, но ни в одном из них не
ограничений будет выполнено.
Попутно отметим следующее обстоятельство. Система уравнений (40) определяет
наилучший набор благ при любом фиксированном количестве Т выделенного
времени; с величиной Т связано лишь численное значение l. Считая величину Т
переменной, введем как в предыдущем пункте, функцию.
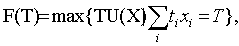
которую можно трактовать как общую полезность времени. Это – “вторичная”
полезность: её величина определяется максимальной полезностью набора благ,
достижимой при данном количестве выделенного времени. Точный смысл
приближенного равенства (31) состоит в том что
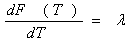
то есть l - предельная полезность времени для Робинзона.
Как мы только что видели, сравнивая l и l' для различных наборов благ, чем
больше Т, тем меньше l. Поскольку природа выделяемого ресурса несущественна,
мы можем сделать следующий общий вывод:
если предельная полезность каждого блага снижается с ростом объема его
потребления, а затраты ресурса пропорциональны объему, то предельная полезность
ресурса падает с увеличением количества используемого ресурса.
Проиллюстрируем эти результаты числовым примером. Допустим, что Робинзон
потребляет 3 вида благ, причем все частные функции полезности имеют один и
тот же вид
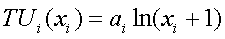
с различными коэффициентами ai. Он может выделить на потребление 15 часов в
сутки; остальные данные приведены в таблице:
Воспользуемся системой (30):
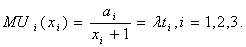
Отсюда
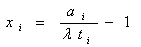
Подставим числовые значения известных параметров:
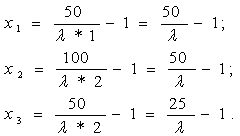
Используем теперь ресурсное ограничение:
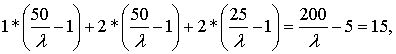
откуда l = 200 / (15 + 5) = 10. Теперь найдем количество каждого блага:
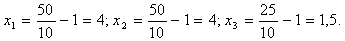
Остальные результаты расчета приведены в таблице:
| i | xi | tixi | TUi | | 1 | 4 | 4 | 80,5 | | 2 | 4 | 8 | 160,9 | | 3 | 1,5 | 3 | 45,8 | | å | | 15 | 287,2 |
9. Взаимные экстремальные задачи
Задачу Лагранжа с одним ограничением можно было бы записать в следующей форме:
f(X) – c ® max
при условии
(41)
h(X) = r.
Вычитание константы с из целевой функции не изменяет положения оптимума.
Лагранжиан этой задачи:
L(X; l) = f(X) - с - l[h(X) - r],
а условия оптимума имеют вид
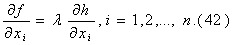
Рассмотрим теперь задачу, в которой целевая и ограничивающая функции
поменялись ролями:
h(X) – r ® min
при условии
(43)
f(X) = с.
Для новой задачи лагранжиан равен
L1(Х; m) = h(Х) - r - m[f(X) - с],
а условие оптимальности –
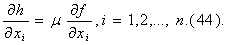
Задачи (41) и (43) называют взаимными по отношению друг к другу. Если,
например, исходная задача состояла в максимизации полезности некоторого
набора продуктов при заданном ресурсном ограничении, то взаимная задача
состоит в минимизации расхода ресурса при обеспечении заданного уровня
полезности.
Сравнение равенств (42) и (43) показывает, что условия оптимальности у обеих
задач одни и те же: достаточно положить m = 1/l, чтобы в этом убедиться. Если
l - предельная полезность ресурса, то m можно было бы назвать “предельной
ресурсоемкостью полезности”.
10. Модель потребительского выбора
Перейдем к рассмотрению рационального потребительского выбора в пространстве
благ с теми же отношениями предпочтения. Введем в рассмотрение функцию
полезности u(Х), согласованную с предпочтениями данного потребителя: u(Х) >
u(у) тогда и только тогда, когда Х ý У. Функцию u(Х) будем считать
непрерывно дифференцируемой.
При этих допущениях моделью потребительского оптимума служит задача Лагранжа
u(Х) ® max
при условии
å рiхi = m,
где рi - цена i - го блага, а m - денежный доход потребителя. Условия
оптимальности имеют вид
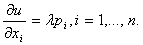
Введем для удобства обозначение 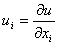 и представим условия оптимальности в форме и представим условия оптимальности в форме
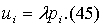
Формально эта система похожа на систему (39), описывающую оптимальность в
задаче о рационе Робинзона. Но здесь имеются и существенные отличия. Во-
первых, теперь мы отказались от предположения о суммируемости полезностей
различных благ, и ui, - не производные полезностей отдельных благ, а лишь
частные производные общей функции полезности. Во-вторых, u(Х) - это не
полезность в некоторой абсолютной количественной шкале, а лишь функция,
согласованная с предпочтениями и отражающая только порядковые отношения. Тем
не менее, перечень аналогичных свойств можно продолжить. Для любой пары благ
(i, j) в точке оптимума должны выполняться соотношения
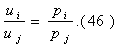
Отметим, что выражение в левой части — это норма замещения i-го блага j-м при
постоянстве объемов всех остальных благ: в пределах поверхности безразличия
должно выполняться равенство
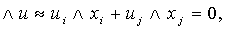
то есть
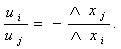
Как мы уже выяснили, значение множителя Лагранжа должно выражать предельную
полезность лимитирующего ресурса, в данном случае - денежного дохода (или,
проще, - предельную полезность денег). Но поскольку значения функции u(Х) не
являются абсолютными значениями полезности, постольку и полная полезность
денег
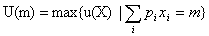
имеет смысл лишь по отношению к выбранной шкале полезностей. То же относится
и к предельной полезности денег.
Что произойдет, если функцию полезности u(Х) заменить равносильной ей функцией u
*(Х)? Отношение предпочтения сохранится, если u*(Х) = j(u(Х)),
где j(u) - монотонно возрастающая функция. Правило дифференцирования сложной
функции позволяет утверждать, что
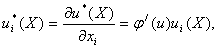
где j'(u) - значение производной dj (u)/du. Заметим, что множитель j(u)
является одним и тем же для всех благ. Поэтому условия оптимальности
ui(Х) = lpi
и
ui(Х) = l рi
определяют одно и то же положение потребительского оптимума в пространстве
благ. Различаются лишь значения множителей Лагранжа:
l = j'(u) l (47)
К этому результату можно подойти с другой стороны. Задавшись некоторым значением
m дохода, при использовании функций u(Х) и u*(Х) мы получим один и тот же
оптимальный набор благ Х0 . Общая полезность денег в одной шкале примет
значение U(m) = u(Х0), в другой 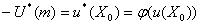
. Таким образом, при любом уровне дохода
U'(m) = j(U(m)), (48)
то есть общие полезности дохода в разных шкалах связаны между собой точно так
же, как и полезности наборов благ. А так как множитель Лагранжа в
рассматриваемой задаче - это предельная полезность денежного дохода, то,
применяя к равенству (48) правило дифференцирования сложной функции, мы снова
придем к равенству (47).
Заметим, что оптимум потребителя не всегда может быть определен в рамках
задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом
потребителя, но и условиями неотрицательности объемов благ:
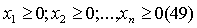
Если на бюджетной поверхности норма замещения каких-либо двух благ всюду
больше или всюду меньше отношения цен, то равенство (46) не может выполняться
ни в одной точке. Задача не имеет внутреннего решения, а имеет угловое
решение. В рамках задачи Лагранжа не могут быть описаны решения, которые
лежат на границах области, определяемой неравенствами.
11. Лабораторные задачи
Задача 1: Некоторое торговое предприятие в течении промежутка времени Т
собирается завести и реализовать некоторый товар R общим объёмом. Стоимость
завоза одной партии равна Сs, а хранение обходится С1. Необходимо определить
оптимальный размер поставки, чтобы суммарный, а так же количество поставок,
интервал времени между поставками и минимальные суммарные издержки. Т.е. надо
найти: qo, no, tso, Qo.
Вариант 1.
T = 24
R = 240000
Cs = 1000
C1 = 30
Вариант 2.
T = 12
R = 15000
Cs = 800
C1 = 60
Вариант 3.
T = 6
R = 9000
Cs = 450
C1 = 20
Вариант 4.
T = 12
R = 9000
Cs = 1200
C1 = 40
Вариант 5.
T = 8
R = 13000
Cs = 900
C1 = 46
Вариант 6.
T = 3
R = 5000
Cs = 300
C1 = 15
Вариант 7.
T = 12
R = 17000
Cs = 1400
C1 = 60
Вариант 8.
T = 6
R = 9000
Cs = 1300
C1 = 30
Вариант 9.
T = 24
R = 250000
Cs = 12000
C1 = 65
Вариант 10.
T = 12
R = 10000
Cs = 3000
C1 = 35
Задача 2: Торговое предприятие намерено завести и реализовать товар n видов
объемами соответственно Rn. Весь объем складских помещений составляет V.
Стоимость хранения одной единицы товара равна C1n. Расходы по завозу Csn. При
этом каждая из n единиц занимает Vn метров. Найти оптимальные размеры
поставок каждого из видов товара.
Вариант 1.
n = 2
R1 = 32000, R2 = 30000;
C11 = 9, C12 = 10;
Cs1 = 1100, Cs2 = 1350;
V1 = 2, V2 = 4;
V = 20000;
Вариант 2.
n = 4
R1 = 4000, R2 = 2000,
R3 = 5000, R4 = 5000;
C11 = 6, C12 = 7, C13 = 9,
C14= 12;
Cs1 = 1100, Cs2 = 1000,
Cs3 = 2000,
Cs4 = 3000;
V1 = 3, V2 = 5, V3 = 5, V3 = 8;
V = 24000;
Вариант 3.
n = 2
R1 = 3500, R2 = 19000;
C11 = 6, C12 = 5;
Cs1 = 1900, Cs2 = 1200;
V1 = 4, V2 = 5;
V = 25000;
Вариант 4.
n = 3
R1 = 4000, R2 = 2000,
R3 = 1000;
C11 = 8, C12 = 8, C13 = 9;
Cs1 = 200, Cs2 = 600, Cs3 = 200;
V1 = 2, V2 = 5, V3 = 3;
V = 9000;
Вариант 5.
n = 2
R1 = 4200, R2 = 2000;
C11 = 6, C12 = 8;
Cs1 = 1500, Cs2 = 1900;
V1 = 3, V2 = 6;
V = 15000;
Вариант 6.
n = 3
R1 = 24000, R2 = 19000,
R3 = 20000;
C11 = 6, C12 = 10, C13 = 10;
Cs1 = 1900, Cs2 = 2000,
Cs3 = 2000;
V1 = 7, V2 = 5, V3 = 5;
V = 30000;
Вариант 7.
n = 3
R1 = 32000, R2 = 5000,
R3 = 21000;
C11 = 8, C12 = 5, C13 = 10;
Cs1 = 1800, Cs2 = 990,
Cs3 = 1000;
V1 = 4, V2 = 2, V3 = 3;
V = 26000;
Вариант 8.
n = 2
R1 = 12500, R2 = 8200;
C11 = 3, C12 = 8;
Cs1 = 900, Cs2 = 1900;
V1 = 3, V2 = 5;
V = 15000;
Вариант 9.
n = 3
R1 = 32000, R2 = 44000,
R3 = 20000;
C11 = 8, C12 = 10, C13 = 15;
Cs1 = 1500, Cs2 = 1900,
Cs3 = 2500;
V1 = 4, V2 = 6, V3 = 8;
V = 20000;
Вариант 10.
n = 2
R1 = 26000, R2 = 17000;
C11 = 6, C12 = 3;
Cs1 = 2100, Cs2 = 1400;
V1 = 6, V2 = 4;
V = 23000.
Список использованной литературы
1. В.И. Варфоломеев “Моделирование элементов экономических систем”.
Москва 2000г.
2. Бусленко Н.П. “Моделирование сложных систем” Москва, 1999г.
3. У. Черчмен, Р. Акоф, Л. Артоф. “Введение в исследование операций”.
Наука: Москва, 1968г.
4. А. Будылин “Элементарные задачи”. Москва, 2002г.
5. Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариацинное “Исчисление и
оптимальное управление”. Москва, 1999г.
6. Ашманов С.А., Тимохов А.В. “Теория оптимизации в задачах и
упражнениях”. Москва, 1991г.
7. “Лабораторный практикум по методам оптимизации”. А.Г.Коваленко,
И.А.Власова, А.Ф.Федечев.- Самара, 1998г.
Страницы: 1, 2, 3, 4, 5
| 


