|
Функции, для которых интеграл Римана существует, называются интегрируемыми в
смысле Римана или, короче, интегрируемыми (R). Для интегрируемости
(R) функции f(x) необходимо, чтобы она была ограниченной.
Еще Коши установил, что всякая непрерывная функция интегрируема (R).
Существуют также и разрывные функции, интегрируемые (R). В частности,
такова любая разрывная монотонная функция.
Легко построить, однако, ограниченную функцию, которая не будет интегрируемой
(R). Рассмотрим, например, функцию Дирихле 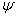
, которая определяется на сегменте [0, 1] следующим образом
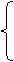 1, если x рационально, 1, если x рационально,
y(x) =
0, если x иррационально.
Легко видеть, что эта функция не интегрируема (R), ибо сумма s
обращается в 0, если все точки x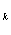
иррациональны и s = 1, если все 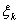
рациональны.
Таким образом, риманово определение интеграла страдает существенными
недостатками - даже очень простые функции оказываются неинтегрируемыми.
Нетрудно разобраться в причинах этого обстоятельства.
Дело заключается в следующем: при составлении сумм Римана s, мы дробим
сегмент [a, b] на мелкие части [x0, x1], [x
1, x2], ¼ ,[xn-1, xn]
(назовем их через e0, e1, ¼ , en
-1), в каждой части ek берем точку xk
и, составив сумму
s = 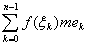 , ,
требуем, чтобы она имела предел, не зависящий от выбора точек xk
в множествах еk. Иначе говоря, каждая точка х из
множества еk может быть взята за xk, а
варьирование этой точки не должно заметно влиять на значение суммы s. А
это возможно лишь в том случае, когда варьирование точки xk
мало изменяет величину f(xk). Но что же объединяет между
собой различные точки х множества ek? Их объединяет
то, что они близки друг другу, ибо еk есть малый сегмент
[xk, xk+1].
Если функция f(x) непрерывна, то достаточная близость абсцисс х
влечет за собой и близость соответствующих значений функции и мы вправе ждать,
что изменение точки xk в пределах множества ek
мало влияет на величину суммы s, но для функция разрывной это вовсе не
так.
Иначе можно сказать, что множества ek составлены так, что
только для непрерывных функций значение f(xk) можно считать
нормальным представителем других значений функции на ek.
Таким образом, самое определение риманова интеграла можно считать вполне
оправданным лишь для функций непрерывных, для прочих же функций оно выглядит
довольно случайным. Ниже мы убедимся, что для интегрируемости (R)
необходимо, чтобы рассматриваемая функция не была «слишком разрывной».
Желая обобщить понятие интеграла на более широкие классы функций, Лебег
предложил другой процесс интегрирования, в котором точки x объединяются
в множества ek не по случайному признаку своей близости на
оси Ох, а по признаку достаточной близости соответствующих значений
функции. С этой целью Лебег разбивает на части не сегмент [a, b],
расположенный на оси абсцисс, а сегмент [А, В], лежащий на оси ординат
и включающий все значения функции f(x):
A = yo < y1 < ¼ < yn = B
Если составить множества ek так:
ek = E(yk £ f < yk+1),
то ясно, что различный точкам х Î еk и в самом деле
отвечают близкие значения функции, хотя, в отличие от римановского процесса,
сами точки x могут быть весьма далеки друг от друга.
В частности, хорошим представителем значений функции на множестве ek
может служить, например, yk, так что естественно положить в
основу понятия интеграла сумму
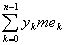 . .
Перейдем теперь к точному изложению вопроса.
Пусть на измеримом множестве E задана измеримая ограниченная функция
f(x), причем
A<f(x)<B.
(1)
Разобьем сегмент [А, В] на части точками
yo = A < y1 < y2 < ¼ < yn = B
и соотнесем каждому полусегменту [уk , уk+1) множество
ek = E(yk £ f < yk+1)
Легко проверить четыре свойства множеств ek:
1) Множества ek попарно не пересекаются: ekek¢ = 0 (k ¹ k').
2) Эти множества измеримы.
3) E = 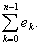
4) тЕ = 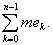
Введем теперь нижнюю и верхнюю суммы Лебега s и S:
S = 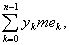 S = S = 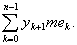
Если мы положим
l = max (yk+1 – yk),
то будем иметь
0 £ S – s £ lmE.
(2)
Основное свойство сумм Лебега выражает
Лемма. Пусть некоторому способу дробления сегмента [А, В]
отвечают суммы Лебега s0 и S0. Если ми добавим
новую точку дробления 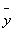
и снова найдем суммы Лебега s и S, то окажется
s0 £ s, S £ S0.
Иначе говоря, от добавления новых точек деления нижняя сумма не уменьшается,
а верхняя не увеличивается.
Доказательство. Допустим, что
yi < 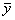
< yi+1.
(3)
Тогда при k ¹ i полусегменты [yk, уk+1),
а с ними и множества ek, фигурируют и в новом способе
дробления. Полусегмент же [yi, yi+1)
при переходе к новому способу заменяется двумя полусегментами
[yi,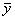 ), [ ), [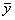 , yi+1), , yi+1),
в связи с чем и множество ei разбивается на два множества
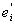 = E(yi £ f < = E(yi £ f < 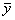 ), ), 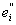 = E( = E(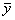 £ f < yi+1). £ f < yi+1).
Очевидно, что
ei =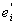 + +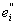 , , 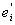 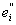 = 0, = 0,
так что
mei = m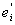
+ m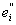 . .
(4)
Из сказанного ясно, что сумма s получается из суммы s0
заменой слагаемого yimei двумя слагаемыми y
im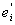 + + 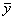
m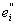 , откуда, в , откуда, в
связи с (3) и с (4), и следует, что s ³ s0.
Для верхних сумм рассуждение аналогично.
Следствие. Ни одна нижняя сумма s не больше ни одной верхней суммы S.
Доказательство. Рассмотрим два каких-нибудь способа дробления I и
II, сегмента [А, В]. Пусть этим способам отвечают соответственно нижние
суммы s1 и s2 и верхние суммы S1
и S2.
Составим третий способ дробления [А, В] - способ III, в котором точками
деления служат точки деления обоих способов I и II. Если способу III отвечают
суммы s3 и S3, то, в силу леммы, s
1 £ s3, S3 £ S2, откуда,
в связи с тем, что s3 £ S3, ясно, что s
1 £ S2, а это и требовалось доказать.
Выберем какую-нибудь определенную верхнюю сумму S0. Так как
для всякой нижней суммы s будет s £ S0, то
множество {s} всех нижних сумм Лебега оказывается ограниченный сверху.
Пусть U есть его точная верхняя граница U = sup{s}.
Тогда, ясно, что
U £ S0.
Ввиду произвольности суммы S0, последнее неравенство
доказывает, что множество {S} всех верхних сумм Лебега ограничено
снизу. Назовем через V его точную нижнюю границу
V = inf{S}.
Очевидно, при любом способе дробления будет
S £ U £ V £ S.
Но, как мы отмечали, S – s £ lmE, откуда
0 £ V – U £ lmE
и, так как l произвольно мало, то
U = V.
Определение. Общее значение чисел U и V называется
интегралом Лебега функции f(x) по множеству Е и
обозначается символом
(L)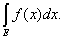
В тех случаях, когда смешение с другими видами интеграла исключено, пишут просто
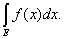
В частности, если Е есть сегмент [а, b], употребляют символы
(L)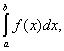 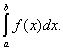
Из сказанного выше следует, что каждая измеримая ограниченная функция
интегрируема в смысле Лебега, или, короче, интегрируема (L). Уже
из этого замечания видно, что процесс интегрирования (L) приложим к
гораздо более широкому классу функций, чем процесс интегрирования (R).
В частности, совершенно отпадают все вопросы, связанные с признаками
интегрируемости, которые для интегралов (R) имеют сравнительно сложный
характер.
Теорема 1. Если l ® 0, то суммы Лебега s и S стремятся
к интегралу 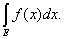
Теорема непосредственно вытекает из неравенств
S £ 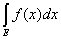 £ S, S – s £ l× mE. £ S, S – s £ l× mE.
Страницы: 1, 2, 3, 4, 5, 6
| 


