|
а стало быть, и тем более
f(x0) - e £ m(x0) £ M(x0) £ f(x0) + e,
откуда, ввиду произвольности e, и вытекает (*). Итак, необходимость
условия (*) доказана.
Пусть теперь, обратно, дано, что (*) выполнено. Тогда, очевидно,
m(x0) = M(x0) = f(x0)
и общее значение функций Бэра в точке x0 конечно.
Возьмем произвольное e > 0 и найдем столь малое d > 0, что
m(x0) - e < md(x0) £ m(x0), M(x0) £ Md(x0) < M(x0) + e.
Эти неравенства означают, что
f(x0) - e < md(x0), Md(x0) < f(x0) + e.
Если теперь x Î (х0 - d, x0 + d), то f(x) лежит между md(x0) и Md(x0), так что
f(x0) - e < f(x) < f(x0) + e.
Иначе говоря, из того, что 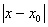 < d вытекает, что < d вытекает, что
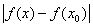 < e, < e,
т. е. функция f(x) непрерывна в точке х0.
Основная лемма. Рассмотрим последовательность дроблений сегмента [а, b]
a = 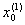 < < 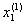 < ¼ < < ¼ < 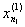 = b = b
. . . . . . . . . . . . . . . . . . . . . . . .
a = 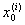 < < 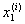 < ¼ < < ¼ < 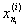 = b = b
. . . . . . . . . . . . . . . . . . . . . . . .
причем при i ® ¥
li = max[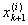 - -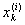 ] ® 0. ] ® 0.
Пусть 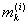 есть точная нижняя граница значений функции f(x) на сегменте есть точная нижняя граница значений функции f(x) на сегменте
[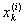 , , 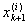 ]. Введем функцию ji(x), полагая ]. Введем функцию ji(x), полагая
ji(x) = 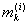 при x Î ( при x Î (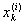 , , 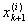 ) )
ji(x) = 0 при x = 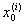 , , 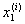 , ¼ , , ¼ , 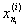 . .
Если х0 не совпадает ни с одной точкой 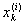
(I = 1, 2, 3, ¼ ; k = 0, 1, 2, ¼ , ni), то
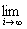 ji(x0) = m(x0). ji(x0) = m(x0).
Доказательство. Фиксируем какое-нибудь i и назовем через
[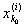 , , 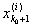
] тот из сегментов i-го способа дробления, который содержит точку
х0. Так как х0 не совпадает ни с одной из
точек деления, то
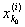 < x0 < < x0 < 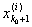
и, следовательно, при достаточно малых d > 0 будет
(х0 - d, x0 + d) Ì [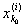 , , 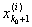 ], ],
откуда следует, что
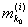 £ md(x0) £ md(x0)
или, что то же самое, что
ji(x0) £ md(x0).
Устремив d к нулю и перейдя к пределу, находим, что при любом i
ji(x0) £ m(x0).
Этим самым лемма уже доказана для случая т(х0) = - ¥. Пусть т(х0) > - ¥ и пусть
h < m(x0).
Тогда найдется такое d > 0, что md(x0) > h.
Фиксировав это d, найдем столь большое i0, что при i > i0 будет
[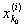 , , 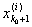 ] Ì (х0 - d, x0 + d), ] Ì (х0 - d, x0 + d),
где, как и выше, [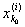
, 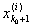 ] есть ] есть
сегмент, содержащий точку х0. Существование такого i
0 следует из условия li ® 0.
Для таких i будет
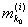 ³ md(x0) > h, ³ md(x0) > h,
или, что то же самое,
ji(x0) > h.
Итак, для всякого h < m(x0) найдется такое i0, что при i > i0
h < ji(x0) £ m(x0),
а это и значит, что ji(x0) ® m(x0). Лемма доказана.
Следствие 1. Функции Бэра т(х) и М(х) измеримы.
В самом деле, множество точек деления {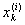
} счетно и, стало быть, имеет меру нуль. Поэтому лемма означает, что j
i(x) ® m(x) почти везде.
Но ji(x) измерима, ибо это ступенчатая функция, значит
измерима я функция т(x). Для верхней функции Бэра М(х)
рассуждение аналогично.
Следствие 2. Если в условиях леммы исходная функция f(x) ограничена, то
(L) 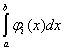 ® (L) ® (L) 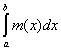 . .
Действительно, если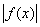 £ K, то, очевидно, £ K, то, очевидно,
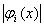 £ K, £ K, 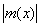 £ K, £ K,
откуда прежде всего следует, что эти функции интегрируемы (L), после
чего остается сослаться на теорему Лебега о предельном переходе под знаком
интеграла.
Перефразируем теперь следствие 2. Для этого заметим, что
(L) 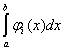 = = 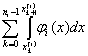 = = 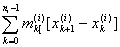 = si, = si,
где si есть нижняя сумма Дарбу, отвечающая i-му
способу дробления. Таким образом, следствие 2 означает, что при i ® ¥
si ® (L) 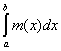 . .
Аналогично можно установить, что верхняя сумма Дарбу Si при
возрастании i стремится к интегралу от верхней функции Бэра
Si ® (L) 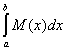 . .
Но в таком случае
Si - si ® (L) 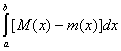 . .
С другой стороны, в курсе Анализа устанавливается, что для того, чтобы
ограниченная функция f(x) была интегрируема (R), необходимо и
достаточно, чтобы было Si – si ® 0.
Сопоставляя это со сказанным выше, мы видим, что для интегрируемости (R)
функции f(x) необходимо и достаточно, чтобы было
(L) 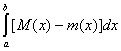 = 0. = 0.
(1)
Условие (1) во всяком случае выполнено, если разность М(х) - т(х)
эквивалентна нулю, но так как эта разность неотрицательна, то и обратно из (1)
следует, что
т(х) ~ М(х).
(2)
Итак, интегрируемость (R) ограниченной функции f(x)
равносильна соотношению (2).
Сопоставив этот результат с теоремой 1, получаем следующую теорему.
Теорема 2 (А. Лебег). Для того чтобы ограниченная функция f(x)
была интегрируема (R),необходимо и достаточно, чтобы она была непрерывна почти
везде.
Эта замечательная теорема представляет собой наиболее простой и ясный признак
интегрируемости (R). В частности, она оправдывает сделанное в пункте 2
замечание, что интегрируемыми (R) могут быть только «не очень
разрывные» функции.
Допустим теперь, что функция f(x) интегрируема (R). Тогда она
необходимо ограничена и почти везде будет
т(х) = М(х).
Но ведь
т(х) £ f(x) £ М(х).
Значит, почти везде
f(x) = m(x),
и f(x), будучи эквивалентна измеримой функции т(х), измерима
сама. Так как всякая ограниченная измеримая функция интегрируема (L),
то такова же и f(x), т. е. из интегрируемости какой-нибудь функции в
смысле Римана вытекает ее интегрируемость в смысле Лебега.
Наконец, из эквивалентности функций f(x) и т(х) следует, что
(L) 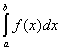 = (L) = (L) 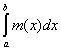 . .
Но, как известно из курса Анализа, в условиях основной леммы для интегрируемой
(R) функции f(x) будет
si ® (R)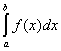 , ,
где si есть нижняя сумма Дарбу, отвечающая i-му
способу дробления. Сопоставляя это с тем, что, как показано нами,
si ® (L) 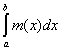 , ,
мы видим, что
(R)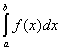 = (L) = (L) 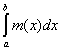 . .
Таким образом, имеет место
Теорема 3. Всякая функция, интегрируемая (R), необходимо
интегрируема и (L), и оба ее интеграла равны между собой.
Страницы: 1, 2, 3, 4, 5, 6
| 


