|
Из этой теоремы, между прочим, следует, что значение интеграла Лебега, которое
в силу самого определения его связано с числами А и В, на самом
деле от них не зависит.
Действительно, допустим, что
A < f(x) < В, A < f(x) <B*,
причем В* < В. Раздробим сегмент [А, В] на части
A = у0 < у1 < ¼ < yn = В,
причем включим и точку В* в число точек деления В* = ут.
Если мы составим множества ek, то легко убедиться, что
ek = 0 (k ³ m).
Значит,
s = 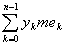 = = 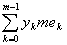 = s*, = s*,
где s* есть нижняя сумма Лебега, построенная, исходя из сегмента
[А, В*]. Сгущая точки дробления и переходя к пределу, найдем, что
I = I*,
где I и I* суть значения интегралов Лебега, отвечающие
сегментам [А, В] и [А, В*]. Таким образом, изменение числа
В не отражается на величине интеграла. То же относится и к числу А.
Этот факт весьма существенен, ибо только теперь определение интеграла
оказывается освобожденным от случайного характера выбора точек А и
В.
3. Основные свойства интеграла
В этом параграфе мы установим ряд свойств интеграла от ограниченной
измеримой функции.
Теорема 1. Если измеримая функция f(x) на измеримом множестве
Е удовлетворяет неравенствам a £ f(x) £ b, то
a× mE £ 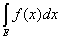 £ b× mE. £ b× mE.
Это теорема обычно называется теоремой о среднем.
Доказательство. Пусть n натуральное число. Если мы положим
A = a - 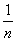 , B = b + , B = b + 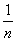 , ,
то окажется, что
A < f(x) < B,
и суммы Лебега можно будет составлять, дробя сегмент [А, В].
Но еслиA £ yk £ B, то, очевидно,
A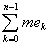 £ £ 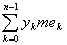 £ B £ B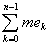
или, что то же самое,
A× mE £ s £ B× mE,
откуда и в пределе
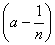 mE £ mE £ 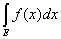 £ £ 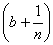 mE. mE.
В силу произвольности числа n, теорема доказана.
Из этой теоремы вытекает несколько простых следствий.
Следствие 1. Если функция f(x) постоянна на измеримом множестве Е и f(x) = с, то
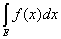 = c× mE. = c× mE.
Следствие 2. Если функция f(x) не отрицательна (не
положительна), то таков же и ее интеграл.
Следствие 3. Если тЕ = 0, то для любой ограниченной
функции f(x), заданной на множестве Е, будет
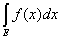 = 0. = 0.
Теорема 2. Пусть на измеримом множестве Е задана измеримая
ограниченная функция f(x). Если множество Е есть сумма конечного числа или
счетного множества попарно не пересекающихся измеримых множеств
E =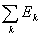 (Ek (Ek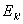 = 0, k ¹ k’), = 0, k ¹ k’),
то
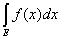 = =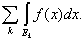
Свойство интеграла, выражаемое этой теоремой, называется его полной
аддитивностью.
Доказательство. Рассмотрим сначала простейший случай, когда число
слагаемых равно двум
Е = 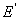 + + 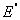 ( (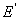 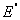 = 0). = 0).
Если на множестве Е
A < f(x) < B
и мы, раздробив сегмент [А, В] точками у0, y1,¼ , уn, составим множества
ek = E(yk £ f < yk+1),
ek’= E’(yk £ f < yk+1),
ek’’= E’’(yk £ f < yk+1),
то, очевидно, будем иметь
ek = ek’ + ek’’ (ek’ek’’ = 0),
откуда
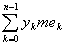 = =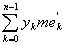 + + 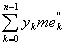
н в пределе, при l ® 0,
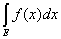 = = 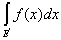 + + 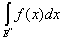
Итак, теорема доказана для случая двух слагаемых множеств. Пользуясь методом
математической индукции, мы легко распространим теорему на случай любого
конечного числа слагаемых множеств.
Остается рассмотреть случай, когда
E = 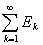 . .
В этом случае
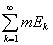 = mE, = mE,
так что при n ® ¥ будет
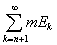 ® 0. ® 0.
(*)
Заметив это, положим
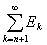 = Rn. = Rn.
Так как для конечного числа слагаемых множеств теорема уже доказана, то
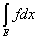 = = 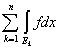 + + 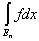 . .
В силу теоремы о среднем
A× mRn £ 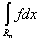 £ B× mRn, £ B× mRn,
а в силу (*) мера mRn множества Rn
стремится к нулю с возрастанием n, откуда ясно, что
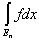 ® 0. ® 0.
Но это и означает, что
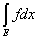 = =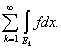
Из этой теоремы вытекает ряд следствий.
Следствие 1. Если измеримые ограниченные функции f(x) и g(x),
заданные на множестве Е, эквивалентны между собой, то
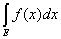 = =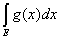 . .
Действительно, если
А = Е(f ¹ g), B = E(f = g),
то mA = 0 и
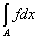 = = 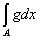 = 0. = 0.
На множестве же В обе функции тождественны и
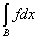 = = 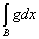 . .
Остается сложить это равенство с предыдущим.
В частности, интеграл от функции, эквивалентной нулю, равен нулю.
Само собою разумеется, что последнее утверждение необратимо. Например, если
f(x) задана на сегменте [-1, +1], так:
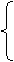 1 при x ³ 0, 1 при x ³ 0,
f(x) =
-1 при x < 0,
то
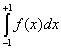 = =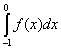 + +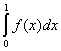 = -1 + 1 = 0, = -1 + 1 = 0,
хотя функция f(x) и не эквивалентна нулю.
Однако справедливо
Следствие 2. Если интеграл от неотрицательной измеримой
ограниченной функции f(x) равен нулю
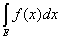 (f(x) ³ 0), (f(x) ³ 0),
то эта функция эквивалентна нулю.
В самом деле, легко видеть, что
E(f>0) = 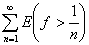 . .
Если бы f(x) не была эквивалентна нулю, то необходимо нашлось бы такое n0, что
mE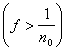 = s > 0. = s > 0.
Полагая
A = E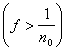 , B = B - A, , B = B - A,
мы имели бы, что
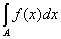 ³ ³ 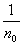 s, s, 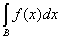 ³ 0, ³ 0,
и, складывая эти неравенства, мы получили бы
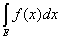 ³ ³ 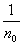 s, s,
что противоречит условию.
Теорема 3. Если на измеримом множестве Q заданы две измеримые
ограниченные функции f(x) и F(x), то
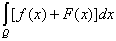 = = 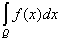 + + 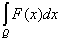 . .
Страницы: 1, 2, 3, 4, 5, 6
| 


