|
тогда сходится ряд: (|un|+un)-|un|=un. Далее, т. к. по св-ву абсолютной
величины |Sn|=|u1+u2+.+un|<=|un| " n Î N, то переходя к пределу
получим:
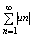 <= <=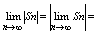 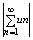
Т2 Если ряд (1) абсолютно сходится, то и любой ряд составленный из тех же
членов, но в любом другом порядке тоже абсолютно сходится и его сумма равна
сумме ряда un – Sn. А вот с условно сходящимися рядами все гораздо
запущенней.
Т(Римана)
Если знакопеременный ряд с действительными членами сходится условно, то каким
бы ни было дейст. число S можно так переставить члены ряда, что его сумма
станет равна S, т. е. сумма неабсолютно сходящегося ряда зависит от порядка
слагаемых
№10
1 Вычисление массы,
координат центра масс,
моментов инерции плоской
материальной пластины с
помощью 2ного интеграла.
Масса плоской пластины вычисляется по ф-ле:
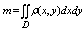 , где r(х, у) – поверхностная плотность. , где r(х, у) – поверхностная плотность.
Координаты центра масс выч по ф-ле:
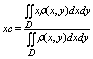
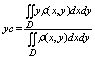
если пластина однородная, т. е. r(х, у) – const, то ф-лы упрощаются:
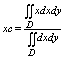 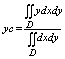
Статические моменты плоскостей фигуры Д относит осей оу и ох
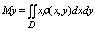 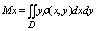
Момент инерции плоской пластины относительно осей ох, оу, начала координат:
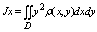 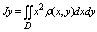 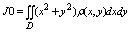
J0=Jx+Jy
если пластина однородная, то ро вышвыривается на фиг и считается равной 1.
2 Сходимость функциональных последовательностей и рядов
Функциональной последовательностью заданной на множестве Е, наз.
последовательность ф-ций {fn(x)} (1)определенных на Е и принимающих числовые
действительные значения.
Пусть задана поледовательность числовых ф-ций {un(x)} Формальнг написанную
сумму: 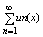 (2) называют (2) называют
функциональным рядом на множестве Е, а ф-цию un(x) – его членами. Аналогично
случаю числовых рядов сумма: Sn(x) = u1(x)+u2(x)+.+un(x) называется частичной
суммой ряда n порядка, а ряд: un+1? un+2. - его n-ным остатком. при каждом
фиксированном х = х0 Î Е получим из (1) числовую последовательность
{fn(x0)}, а из (2) – числовой ряд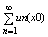
, которые могут сходится или расходится. если кто-нибудь из оных сходится, то
сходится и функциональная посл (1) в т х0, и сия точка наз. точкой сходимости.
Если посл(1) сход на м-ж Е, то ф-ция f, определенная при " x Î E f(x) = 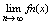
назывется пределом посл (1), если ряд(2) сходится на м-ж Е, то ф-ция S(x)
определенная при " x Î Е равенством
S(x)= 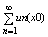
называется суммой ряда (2).
Остаток ряда сходится только когда на этом же м-ж сходится сам ряд., если
обозначить сумму остатка ряда через rn(ч), то S(x) = Sn(x)+rn
(x)
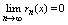 Если ряд (2) Если ряд (2)
сходится абсолютно, то он наз абсолютно сходящимся на м-ж Е. Множество всех
точек сходимости функционального ряда наз областью сходимости. Для определения
области сходимости можно использовать признак Даламбера и Коши. С ихнею помашшю
ф-ц ряд исследуется на абсолютную сходимость Например, если существует
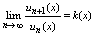 и и
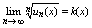 , то ряд (2) абсолютно сходится при k(x)<1 и расходится при k(x)>1. , то ряд (2) абсолютно сходится при k(x)<1 и расходится при k(x)>1.
№11
1 Тройные интегралы
Пусть на некоторой ограниченной замкнутой области V трехмерного пространства
задана ограниченная ф-ция f (x,y,z). Разобьем область V на n произвольных
частичных областей, не имеющих общих внутренних точек, с объемами DV1. DVn В
каждой частичной области возбмем произв. точку М с кооорд Mi(xi,hi,ci) составим
сумму: 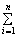
f(xi,hi,ci)×DVi, кот наз интегральной суммой для ф-ции f(x,y,z). Обозначим
за l максимальный диаметр частичной области. Если интегральная сумма при l
à 0 имеет конечный предел, то сей предел и называется тройным интегралом
от ф-ции f(x,y,z) по области V И обозначается:
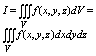
2 Равномерная
сходимость функциональных
последовательностей и рядов.
Признак Вейерштрасса.
Ф-циональную последовательность {fn)x)} x Î E наз. равномерно сходящейся
ф-цией f на м-ж Е, если для Î e >0, сущ номер N, такой, что для " т х
Î E и " n >N выполняется ¹-во: |fn(x)-f(x)|<e. Если м-ж
{fn)x)} равномерно сходится на м-ж Е, то она и просто сходится в ф-ции f на сем
м-ж. тогда пишут: fn à f.
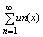 наз. равномерно наз. равномерно
сходящимся рядом, если на м-ж Е равномерно сходится последовательность его
частичной суммы. , т. ен. равномерная сходимость ряда означает:Sn(x) à
f(x) Не всякий сходящийся ряд является равномерно сходящимся, но всякий
равномерно сходящийся – есть сходящийся (не, вот это наверное лет 500
выдумывали.)
Т. (Признак Вейерштрасса равномерной сходимости ряда)
Если числовой ряд: 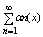 (7), (7),
где a >=0 сходится и для " x Î E и " n = 1,2. если выполняется нер-во
|un(x)|<=an(8), ряд 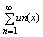
(9) наз абсолютно и равномерно сходящимся на м-ж Е.
Док-вы:
Абсолютная сходимость в каждой т. х следует из неравенства (8) и сходимости
ряда (7). Пусть S(x) – сумма ряда (9), а Sn(x) – его частичная сумма.
Зафиксируем произвольное e >0 В силу сходимости ряда (7) сущ. номера N, " n
>N и вып. нерво 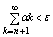
Следовательно: |S(x)-Sn(x)| = 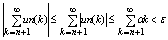
Это означает, что Sn(x) à S(x) что означает равномерную сходимость ряда..
№12
1 Замена переменных
в тройном интеграле.
Если ограниченная замкнутая область пространства V = f(x,y,z) взаимно
однозначно отображается на область V’ пространства = (u,v,w) Если непрерывно
дифференцируемы функции: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) и существует
якобиан
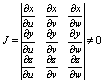
то справедлива формула:
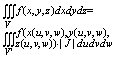
При переходе к цилиндрическим координатам, с вязанными с x,y,z формулами:
x=rcosj, y=rsinj, z=z (0<=r<=+¥, 0<=j <= 2p,
-¥<=z<=+¥)
Якобиан преобразования:
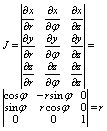
И поэтому в цилиндрических координатах переход осуществляется так:
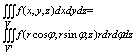
При переходе к сферическим координатам: r? j q, связанными с z,y,z формулами
x=rsinq×cosj,
y=r sinqsinj, z=rcosq.
(0<=r<=+¥, 0<=j <= 2p,
0<=q <=2p)
Якобиан преобразования:
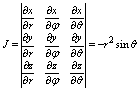
Т. е. |J|=r2×sinq.
Итак, в сферических координатах сие будет:
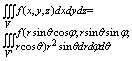
2 Свойства равномерно
сходящихся рядов
Т1 Если ф-ция un(x), где х Î Е непрерывна в т. х0 Î E и ряд 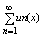
(1) равномерно сходится на Е, то его сумма S(x) = 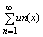
Страницы: 1, 2, 3, 4, 5, 6
| 


