|
остаточным членом ф-лы Тейлора в интегральной форме. Ф-ла (9) – формулой
Лагранжа.
Преобразуя ф-лу Тейлора при х0 = 0 получаем ф-лу Маклорена.
Т3 Если ф-ция f(x) имеет в окрестности т х0 производные любого порядка и все
они ограниченны одним и тем же числом С, т е " x Î U(x0) |f(
n)(x)|<=C, то ряд Тейлора этой ф-ции сходится в ф-ции f(x)
для всех х из этой окрестности.
№17
1 Формула Грина
Сия очень полезная в сельском хозяйстве формула устанавливает связь между
криволинейными и двойными интегралами.
Пусть имеется некоторая правильная замкнутая область Д, ограниченная контуром L
и пущая ф-ции P(x,y) и Q(x,y) непрерывны вместе со своими частными
производными: 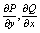 в в
данной области. тогда имеет место ф-ла:
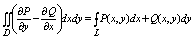
И вот вся эта фигулина и есть формула Грина.
Контур L определяющий область д может быть задан показательными уравнениями х =
х1(у), х=х2(у) с<=y<=d x1(y)<=x2(y) или
y = y1(x), y=y2(x) a<=x<=b y1(x)<=y2(x).
Рассмотрим область Д ограниченную неравенствами: a<=x<=b и
y1(x)<=y2(x). и преобразуем двойной интеграл 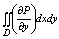
к криволинейным для чего сведем его к повторному и ф-ле Невтона-Лыебница
выполним интегрирование по у и получим:
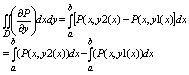 каждый из 2 каждый из 2
определенных интегралов в правой части последнего равенства = криволинейному
интегралу 2 рода взятому по соответствующей кривой а именно:
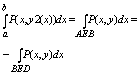
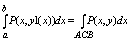
Итак двойной интеграл: 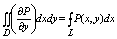
Формула Грина остается справедливой для всякой замкнутой области Д, которую
можно разбить проведением дополнительных линий на конечной число правильных
замкнутых областей.
2 Разложение элементарных ф-ций в ряд Тейлора (Маклорена)
1Разложение ф-ции ех
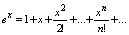 ряд Маклорена. ряд Маклорена.
радиус сходимости:
R=¥ следовательно ряд абсолютно сходится на всей числовой прямой.
2Разложение sinx и cosx В степенной ряд Маклорена
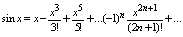
сходится на всей числовой оси
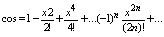 сходится на всей числовой оси сходится на всей числовой оси
3. f(x) = (1+x)a
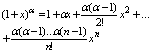
Наз. биномиальный ряд с показателем a Различают 2 случая:
1- a Î N, тогда при любом х все члены ф-лы исчезают, начиная с (a +2)
поэтому ряд Маклорена содержит конечное число членов и сходится при всех х.
Получается формула Бинома Невтона: 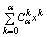
, где 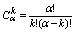 биномиальный биномиальный
коэффициент.
2- a Î R>N (a ¹ 0 х ¹ 0) и ряд сходится абсолютно при |x|>1
4 Разложение ф-ции ln(1+x)
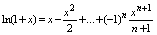
сходится при –1<x<=1
5 Разложение arctgx в степенной ряд Маклорена
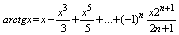 сходится при -1<=x<=1 сходится при -1<=x<=1
№18
1 Некоторые приложения криволинейных интегралов 1 рода.
1.Интеграл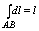 - длине дуги АВ - длине дуги АВ
2.Механический смысл интеграла 1 рода.
Если f(x,y) = r(x,y) – линейная плотность материальной дуги, то ее масса: 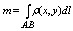
для пространственной там буква зю добавляется.
3.Координаты центра масс материальной дуги:
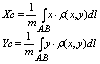
4. Момент инерции дуги лежащей в плоскости оху относительно начала координат
и осей вращения ох, оу:
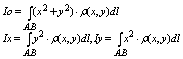
5. Геометрический смысл интеграла 1 рода
Пусть ф-ция z = f(x,y) – имеет размерность длины f(x,y)>=0 во всех точках
материальной дуги лежащей в плоскости оху тогда:
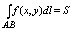 , где S – площадь , где S – площадь
цилиндрической поверхности, кот состоит из перпендикуляров плоскости оху, восст
в точках М(x,y) кривой АВ.
2 Геометрические и арифметические ряды.
№19
1 Некоторые приложения криволинейных интегралов 2 рода.
Вычисление площади плоской области Д с границей L
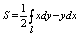
2.Работа силы. Пусть материальная т очка под действием силы перемещается
вдоль непрерывной плоской кривой ВС, направясь от В к С, работа этой силы:
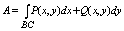
при пространственной кривой там исчо третья функция появитца для буквы зю.
2 Свойства сходящихся рядов
№20
1 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
Плоская область W наз односвязной если не имеет дыр. т. е. однородная.
Пусть ф-ция P(x,y) и Q(x,y)вместе со своими частными производными непрерывны
в некоторой замкнутой, односвязной области W тогда следующие 4 условия
эквиваленты, т. е. выполнение какого либо из них влечет остальные 3.
1. Для " замкнутой кусочногладкой кривой L в W значение криволинейного
интеграла:
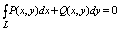
2. Для все т. А и т. В области W значение интеграла 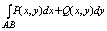
не зависит от выбора пути интегрирования, целиком лежащего в W.
3. Выражение Pdx+Qdy представляет собой полный дифференциал некоторых функций
определенных в W существует ф-ция E=c(х,у) опред в W такая, что dE = Pdx+Pdy
4. В области W 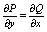
Отседова следовает, что условие 3 является необходимым и достаточным условием
при котором интегралы 2 рода не зависят от выбора пути интегрирования.
2 Интегральный признак сходимости ряда. Ряд Дирихле.
№21
1 Интегрирование в полных дифференциалах
Пущай ф-ция P(x,y) и Q(x,y) 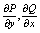
- непрерывны в замкнутой области W и выражение P(x,y) + Q(x,y) есть полный
дифееренциал некоторой ф-ции F(x,y) в W , что равносильно условию: 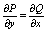
, тогда dF=Pdx+Qdy.
Для интегралов независящих от пути интегрирования часто применяют обозначение:
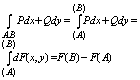
или
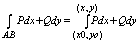
А(x0,y0) Î l , В = (х,у) Î l
поэтому
F(x,y)=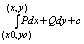
где (х0,у0) – фиксированная точка Î l, (x,y) – произвольная точка
Î l , с – const. и дает возможность определить все ф-ции, имеющие в
подинтегральном выражении свои полные дифференциалы. Тк. интеграл не зависит
от пути интегрирования, за путь инт. удобно взять ломаную звень которой
параллельны осям координат. тогда формула преобразуется к виду.
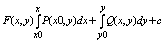 2 Признаки сравнения 2 Признаки сравнения
№22
1 Сведение 2-ного интеграла к повторному
Пусть у1(х), у2(х) непрерывны на отрезке [a, b], у1(х)<= у2(х) на всем отрезке.
D={x,y}: a<=x<=b; y1(x)<=y<=y2(x)
Отрезок [a,b] – проекция Д на ось ох. Для такой области людбая прямая,
параллельная оу и проходящая через внутреннюю точку области Д пересекает
границу области не более чем в 2 точках. Такая область наз. правильной в
направлении оси оу.
Если фция f(x,y) задана на Д и при каждом х Î [a,b] непрерывна на у , на
отрезке, [y1(x),y2(x)], то фц-ия F(x) = 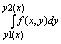
, наз. интегралом, зависящим от параметра I, а интеграл : 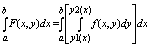
, наз повторным интегралом от ф-ции f(x,y) на области Д. Итак, повторный
интеграл вычисляется путем последовательного вычисления обычных определенных
интегралов сначала по одной., а затем по другой переменной.
2 Признаки Даламбера и Коши
№23
1 2 ной интеграл
в полярных координатах
Переход к полярным координатам частный случай замены переменных.
Луч, проходящий из произв точки О имеет на плоскости полярные координаты A(r, j)
где r = |ОA| расстояние от О до А полярный радиус. j = угол между
векторами ОА и ОР – полярный угол отсчитываемой от полярной оси против часовой
стрелки. всегда 0<=r<=+¥, 0<=j <=2p .
Зависимость между прямоугольными и полярными координатами: x = r×cosj , y
= r×sinj .
Якобиан преобразования будет равен:
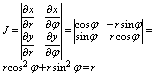
И формула при переходе примет вид:
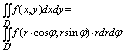
2 Знакочередующиеся ряды признак Лейбница
№24
1 Замена переменных
в тройном интеграле
Если ограниченная замкнутая область пространства V = f(x,y,z) взаимно
однозначно отображается на область V’ пространства = (u,v,w) Если непрерывно
дифференцируемы функции: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) и существует
якобиан
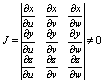
то справедлива формула:
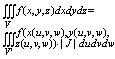
При переходе к цилиндрическим координатам, с вязанными с x,y,z формулами:
x=rcosj, y=rsinj, z=z (0<=r<=+¥, 0<=j <= 2p,
-¥<=z<=+¥)
Якобиан преобразования:
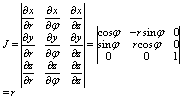 И поэтому в цилитндрических координатах переход осуществляется так: И поэтому в цилитндрических координатах переход осуществляется так:
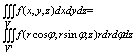
При переходе к сферическим координатам: r? j q, связанными с z,y,z формулами
x=rsinq×cosj,
y=r sinqsinj, z=rcosq.
(0<=r<=+¥, 0<=j <= 2p,
0<=q <=2p)
Якобиан преобразования:
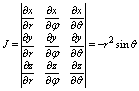
Т. е. |J|=r2×sinq.
Итак, в сферических координатах сие будет:
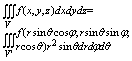
2 Радиус сходимости и интервал сходимости степенного ряда
№25
1 Условия существования и вычисления криволинейных интегралов
Кривая L наз. гладкой, если ф-ции j(t), y(t) из определяющих её
параметрических уравнений:
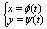 (1) (1)
имет на отрезке [a,b] непрерывные производные: j’(t), y’(t).Точки кривой L наз
особыми точками, если они соответствуют значению параметра t Î [a,b] для
которых (j’(t))2+(y’(t))2 = 0 т. е. обе производные
обращаются в 0. Те точки для которых сие условие не выполняется наз. обычными
(ВАУ!).
Если кривая L=AB задана ф-лами (1), является гладкой и нет имеет обычных
точек, а ф-ции f(x,y), P(x,y), Q(x,y) непрерывны вдоль этой кривой, то
криволинейные интегралы всех видов существуют (можно даже ихние формулы
нарисовать для наглядности) и могут быть вычислены по следующим формулам
сводящим эти интегралы к обычным:
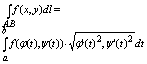
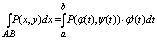
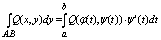
Отседова жа вытекаает штаа:
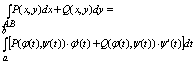
В частности, если кривая АВ задана уравнением y = y(x), a<=x<=b , где у(х)
непрерывно дифференцируемая ф-ция, то принимая х за параметр t получим: 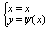
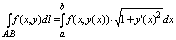
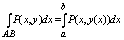
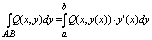 ну и сумма там тожжа упростица. ну и сумма там тожжа упростица.
ну и наоборот тожжа так будит, если х = х(у)
Если АВ задана в криволинейных координатах a <= j <= b где ф-ция r(j)
непрерывно дифференцируема на отрезке [a, b] то имеет место частный случай, где
в качестве параметра выступает полярный угол j. x = r(j)×cos(j),
y= r(j)×sin(j).
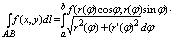
и у второго рода так же.
Прямая L наз кусочно гладкой, если она непрерывна и распадается на конечное
число не имеющих общих внутренних точек кусков, каждый из которых
представляет собой гладкую кривую. В этом случает криволинейные интегралы по
этой кривое определяются как сумма криволинейных интегралов по гладким кривым
составляющим сию кусочно-гладкую кривую.
все выше сказанное справедливо и для пространственной кривой (с буквой зю).
2 Разложение элементарных ф-ций в ряд Тейлора (Маклорена).
Страницы: 1, 2, 3, 4, 5, 6
| 


