|
также непрерывна в т. х0.
Т2 (Об поюленном интегрировании ряда)
Пусть сущ. ф-ция un(x) Î R и непрерывная на отр. [a,b] и ряд 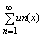
(3) равномерно сходится на этом отрезке, тогда какова бы ни была т. х0 Î
[a, b] 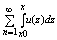 (4) тоже (4) тоже
равномерно сходится на [a,b]. В частности: при x0 = a, х = b: 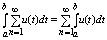
т. е. ряд (3) можно почленно интегрировать.
Т3 (о почленном дифференцировании ряда)
Пусть сущ. ф-ция un(x) Î R и непрерывная на отр. [a,b] и ряд её
производных 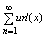 (6) (6)
равномерно сходящийся на отр [a,b] тогда, если ряд 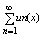
сходится хотя бы в одной точке x0 Î [a,b] то он сходится равномерно на
всем отрезке [a,b], его сумма S(x) = 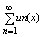
является непрерывно дифференцируемой ф-цией и
S’(x)= 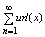 (9) (9)
В силу ф-л ы (8) последнее равенство можно записать:
(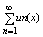 )’ = )’ = 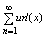
So ряд (7) можно почленно дифференцировать
№13
1 Приложения
тройных интегралов
Объем тела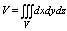
Масса тела: 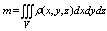 , где r(М) = r(x,y,z) - плотность. , где r(М) = r(x,y,z) - плотность.
Моменты инерции тела относительно осей координат:
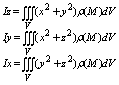
Момент инерции относительно начала координат:
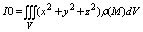
Координаты центра масс:
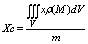
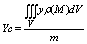
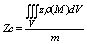 m – масса. m – масса.
Интегралы, стоящие в числителях выражают статические моменты тела: Myz, Mxz,
Mxy относит коорд плоскостей oyz, oxz, oxy. Если тело однородное: r(М) =
const, то из формул она убирается и оне упрощаются как в 2ных интегралах.
2 Степенные ряды. Теорема Абеля
Степенным рядом наз функциональный ряд вида: a0+a1x+a
2x2+. + anxn = 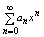
(1) x Î R членами которого являются степенные ф-ции. Числа an Î R,
наз коэффициентами ряда(1). Степенным рядом наз также ряд:
a0+a1(x-x0)+a2(x-x0)2. + an(x-x0)n = 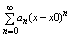 (2) (2)
Степенной ряд (1) сходится абсолютно по крайней мере в т. х = 0, а ряд (2) в
т х = х0, т .е в этих случаях все лены кроме 1 равны 0. Ряд (2) сводится к
ряду (1) по ф-ле у = х-х0.
Т Абеля
1Если степенной ряд (1) сходится в т. х0 ¹ 0, то он сходится абсолютно при
любом х, для которого |x|<|x0|.
2Если степеннгой ряд (1) расходится в т. х0, то он расходится в любой т. х, для
которой |x|>|x0|
№14
1 Определение криволинейных
интегралов 1 и 2 рода
Криволинейный интеграл по длине дуги (1 рода)
Пусть ф-ция f(x,y) определена и непрерывна в точках дуги АВ гладкой кривой К.
Произвольно разобъем дугу на n элементарных дуг точками t0..tn пусть Dlk
длина k частной дуги. Возьмем на каждой элементарной дуге произвольную точку
N(xk,hk) и умножив сию точку на соотв. длину дуги составим три интегральную
суммы:
d1 =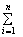 f(xk,hk)×Dlk f(xk,hk)×Dlk
d2 =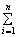 Р(xk,hk)×Dхk Р(xk,hk)×Dхk
d3 =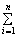 Q(xk,hk)×Dyk, Q(xk,hk)×Dyk,
где Dхk = xk-xk-1, Dyk = yk-yk-1
Криволинейным интегралом 1 рода по длине дуги будет называться предел
интегральной суммы d1 при условии, что max(Dlk) à 0
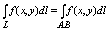
Если предел интегральной суммы d2 или d3 при l à 0, то этот предел наз.
криволинейным интегралом 2 рода, функции P(x,y) или Q(x,y) по кривой l = AB и
обозначается:
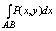 или или 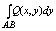
сумму: 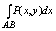 + +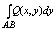
принято называть общим криволинейным интегралом 2 рода и обозначать символом:
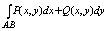 в этом случае ф-ции в этом случае ф-ции
f(x,y), P(x,y), Q(x,y) – называются интегрируемыми вдоль кривой l = AB. Сама
кривая l наз контуром или путем интегрирования А – начальной, В – конечной
точками интегрирования, dl – дифференциал длины дуги, поэтому криволинейный
интеграл 1 рода наз. криволинейным интегралом по дуге кривой, а второго рода –
по функции..
Из определения криволинейных интегралов следует, что интегралы 1 рода не
зависят от того в каком направлении от А и В или от В и А пробегается кривая
l. Криволинейный интеграл 1 рода по АВ:
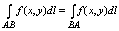 , для криволинейных , для криволинейных
интегралов 2 рода изменение направления пробегания кривой ведет к изменению
знака:
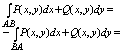
В случае, когда l – замкнутая кривая т. е. т. В совпадает с т. А, то из двух
возможных направлений обхода замкнутого контура l называют положительным то
направление, при котором область лежащая внутри контура остается слева по
отношению к ??? совершающей обход, т. е. направление движения против часовой
стрелки. Противоположное направление обхода наз – отрицательным.
Криволинейный интеграл АВ по замкнутому контуру l пробегаемому в положит
направлении будем обозначать символом:
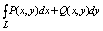
Для пространственной кривой аналогично вводятся 1 интеграл 1 рода:
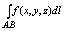 и три интеграла 2 рода: и три интеграла 2 рода:
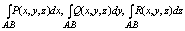
сумму трех последних интегралов наз. общим криволинейным интегралом 2 рода.
2 Радиус сходимости и интервал сходимости степенного ряда.
Рассмотрим степенной ряд:
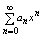 (1) Число (конечное (1) Число (конечное
или бесконечное) R>=0 наз радиусом сходимости ряда (1) если для любого х
такого, что |x|<R ряд (1) сходится, а для " х таких. что |x|>R ряд
расходится Интервал на числовой оси состоящий из т. х для которых |x|<R, т.
е. (-R, +R) наз. интервалом сходимости.
Т1 Для всякого степенного ряда (1) существует радиус сходимости R
0<=R<=+¥ при этом, если |x|<R, то в этой т. х ряд сходится
абсолютно
Если вместо х взять у = х-х0, то получится: интервал сходимости: |x-x0<R|
будет: (x0-R, x0+R)При этом если |x-x0|<R? то ряд сходится в т. x абсолютно
иначе расходится. На концах интервала, т. е. при x = -R, x=+R для ряда (1) или
x = x0-R, x=x0+R для ряда (3) вопрос о сходимости решается индивидуально. У
некоторых рядов интервал сходимости может охватывать всю числовую прямую при R
= +¥ или вырождаться в одну точку при R = 0.
Т2 Если для степенного ряда (1) существует предел (конечный или бесконечный): 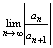
, то радиус сходимости будет равен этому пределу.
Док-вы: Рассмотрим ряд из абсолютных величин 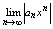
и по Даламберу исследуем его на сходимость:
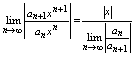 (5) (5)
1)Рассмотрим случай, когда 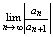
конечен и отличен от 0. Обозначив его через R запишем (5) в виде 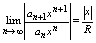
При числовом значении х степенной ряд становится числовым рядом, поэтому по
Страницы: 1, 2, 3, 4, 5, 6
| 


