|
Даламберу ряд (1) сходится если |x|/R<1, т. е. |x|<R, тогда по признаку
абсолютной сходимости ряд (1) сходится абсолютно при |x|<R иначе ряд
расходится.
2)Пусть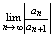 = ¥ = ¥
тогда из(5) следует, что 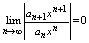
для любого х Î R Итак ряд (1) сходится при любом х причем абсолютно.
3) Пусть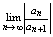 =0 тогда из =0 тогда из
(5) следует, что 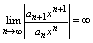 и и
ряд расходится для любого х. Он сходится только при х = 0 В этом сл-е R = 0.
Т3 Если существует предел конечный или бесконечный 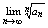 , то , то 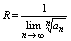 (10) (10)
№15
1 условия
существования и вычисления
криволинейных интегралов.
Кривая L наз. гладкой, если ф-ции j(t), y(t) из определяющих её
параметрических уравнений:
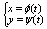 (1) (1)
имеет на отрезке [a,b] непрерывные производные: j’(t), y’(t).Точки кривой L наз
особыми точками, если они соответствуют значению параметра t Î [a,b] для
которых (j’(t))2+(y’(t))2 = 0 т. е. обе производные
обращаются в 0. Те точки для которых сие условие не выполняется наз. обычными
(ВАУ!).
Если кривая L=AB задана ф-лами (1), является гладкой и нет имеет обычных
точек, а ф-ции f(x,y), P(x,y), Q(x,y) непрерывны вдоль этой кривой, то
криволинейные интегралы всех видов существуют (можно даже ихние формулы
нарисовать для наглядности) и могут быть вычислены по следующим формулам
сводящим эти интегралы к обычным:
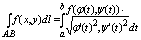
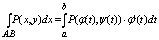
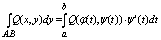
Отседова жа вытекаает штаа:
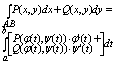
В частности, если кривая АВ задана уравнением y = y(x), a<=x<=b , где у(х)
непрерывно дифференцируемая ф-ция, то принимая х за параметр t получим: 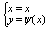
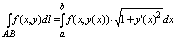
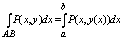
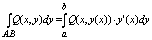
ну и сумма там тожжа упростица.
ну и наоборот тожжа так будит, если х = х(у)
Если АВ задана в криволинейных координатах a <= j <= b где ф-ция r(j)
непрерывно дифференцируема на отрезке [a, b] то имеет место частный случай, где
в качестве параметра выступает полярный угол j. x = r(j)×cos(j),
y= r(j)×sin(j).
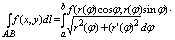
и у второго рода так же.
Прямая L наз кусочно-гладкой, если она непрерывна и распадается на конечное
число не имеющих общих внутренних точек кусков, каждый из которых
представляет собой гладкую кривую. В этом случает криволинейные интегралы по
этой кривое определяются как сумма криволинейных интегралов по гладким кривым
составляющим сию кусочно-гладкую кривую. все выше сказанное справедливо и для
пространственной кривой (с буквой зю).
2 Свойства степенных рядов
Т1 Если степенной ряд 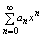
(1) имеет радиус сходимости R>0, то на любом отрезке действительной оси вида
|x|<=r, 0<r<R (2) (или [-r,r]) целиком лежащем внутри интервала
сходимости ряд (1) сходится равномерно.
Для ряда 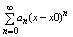 отрезком отрезком
равномерной сходимости будет отрезок |x-x0|<=r или ([x0-r,x0+r])
Т2 На любом отрезке |x-x0|<=r сумма степенного ряда является непрерывной ф-цией.
Т3 Радиусы сходимости R, R1, R2 соответственно рядов× 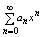
(5), 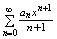 (6), (6), 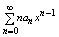
(7) равны: R1=R2=R3. Итак ряды (6) и (7) полученные с помощью формального
интегрирования и дифференцирования имеют те же радиусы сходимости, что и
исходный ряд.
Пусть ф-ция f(x) является суммой степенного ряда  (9) (9)
Т4 Дифференцирование степенного ряда
Если ф-ция f(x) на интервале (x0-R, x0+R) является суммой ряда (9), то она
дифференцируема на этом интервале и её производная f’(x) находится
дифференцированием ряда (9):
f’(x)= 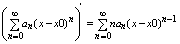 При этом радиус сходимости полученного ряда = R При этом радиус сходимости полученного ряда = R
Т5 О интегрировании степенного ряда
Степенной ряд (9) можно почленно интегрировать на любом отрезке целиком
принадлежащем интервалу сходимости при этом полученный степенной ряд имеет
тот же радиус сходимости что и исходный ряд.
Последовательное применение Т4 приводит к утверждению, что ф-ция f имеет на
интервале сходимости производные всех порядков, которые могут быть найдены из
ряда (9) почленным дифференцированием. При интегрировании и дифференцировании
степенного ряда внутри интервала сходимости радиус сходимости R не меняется,
однако на концах интервала может изменяться.
№16
1 Свойства криволинейных интегралов
Св-ва криволинейных интегралов 1 рода:
1.Константа выносится за знак интеграла, а интеграл суммы можно представить в
виде суммы интегралов:
2. Если дуга АВ состоит из двух дуг Ас и Св не имеющих общих внутренних точек
и если для ф-ции f(x,y) сущ криволинейный интеграл по АВ, то для для сей ф-
ции сущ криволинейные интегралы по АС и по ВС причем:
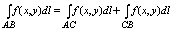
3. 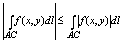
4.Ф-ла среднего значения
если ф-ция f(x,y) непрерывна вдоль кривой АВ, то на этой кривой найдется
точка М, такая, что:
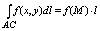 , где l – длина кривой , где l – длина кривой
Криволинейный интеграл 2 рода обладает всеми свойствами интегралов 1 рода, и
исчо при изменении направления прохождения кривой он меняет знак. .И вапще
все сказанное выше справедливо и для пространственной кривой (этта та которая
с буквой зю)
2 Разложение ф-ций в степенные ряды. Ряды Тейлора и Маклорена.
Пусть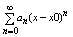 (1) сходится при (1) сходится при
|x-x0|<R а его сумма является ф-лой f(x)= 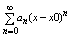
(2) В этом случае говорят, что ф-ция f(x) разложена в степенной ряд. (1) .
Т1 Если ф-ция f распространяется в некоторой окрестности т. х0 f(x)= 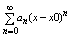 , то , то 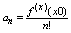
и справедлива формула:  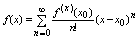
(15) Если в некоторой окрестности заданной точки ф-ция распадается в степенной
ряд, то это разложение единственно.
Пусть дествит. ф-ция f определена в некоторой окрестности т. х0 и имеет в этой
точке производные всех порядков, тогда ряд: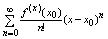
(6) наз рядом Тейлора ф-ции f в т, х0
При х0=0 ряд Тейлора принимает вид:
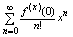 (6’) и называется ряд Маклорена. (6’) и называется ряд Маклорена.
Ряд Тейлора может:
1 Расходится всюду, кроме х=х0
2 Сходится, но не к исходной ф-ции f(x), а к какой-нибудь другой.
3 Сходится к исходной ф-ции f(x)
Бесконечная дифференцируемость ф-ции f(x) в какой-то т. х0 является
необходимым условием разложимости ф-ции в ряд Тейлора, но не является
достаточным. Для введения дополнительных условий треб. ф-ла Тейлора.
Т2 Если ф-ция f(x) (n+1) раз дифференцируема на интервале (x0-h, x0+h) h>0,
то для всех x Î (x0-h, x0+h) имеет место ф-ла Тейлора:
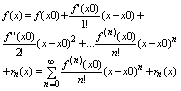 где остаток rn(x) можно записать: где остаток rn(x) можно записать:
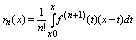 (8) (8)
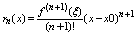 (9) Формула (8) наз (9) Формула (8) наз
Страницы: 1, 2, 3, 4, 5, 6
| 


