Лекция: Математический анализ

1.Счетные и несчетные множества. Счетность множества рациональных чисел.

Множество - совокупность некоторых объектов

Элементы множества - объекты составляющие множество

Числовые множества - множества элементами которых являются числа.

Задать множество значит указать все его элементы:

1 Способ: А={а: Р(а)} эти записи Читать- множество тех а таких что...

A={а-Р(а)} равноценны

Р(а) - предикат = высказывание об элементе, бывает ложно или истинно по

отношению к кокретному элементу. Множество А состоит из тех а для которых

предикат истина.

2 Способ: Конструирование из других множеств:

AÚB = {c: cÎA Ú cÎB}, AÙB = {c: cÎA

Ù cÎB}, A\ B = {c: cÎA Ù сÏB}

U - универсальное множество (фиксированное)

U³A; U \ A = A’ = cA (A’ - дополнение множества A)

Свойства:

1. AÚ(BÚC)=(AÚB) ÚC - ассоциативность;

AÚB=BÚA - коммутативность; AÚÆ=A; AÚU=U

2. AÚ (BÙC)=(AÚB) Ù(AÚC) & AÙ (BÚC)=(AÙB) Ú(AÙC) - дистрибутивность; АÙÆ=А

A” =A - закон исключающий третьего (AÚB)’=A’ÙB’;

(AÙB)’=A’ÚB’; AÙA’= Æ

Иллюстрация свойств: Диаграммы Эйлера-Венна.

"=>" cÎ(AÚB)’ => cÏAÚB => cÏA & cÏB => cÎ A’ & cÎB’ => cÎA’ÙB’

"<=" cÎA’ÙB’ => cÎA’ & cÎB’ => cÏA & cÏB => cÏAÚB => cÎ(AÚB)’

Отображение множеств:

f:A®B (на множестве А задано отображение f со значением множества B)

aÎA; bÎB => b - образ элемента а при отображении f; a - прообраз

элемента b при отображении f

Так как для каждого элемента из А ставится в соответствие элемент из В, значит

А - область определения (Dom f=А), а область значенийB (Im f £B)

Для отображения задают: 1) способ 2) Dom 3) Im

Отображение f инъективно если f(x)=f(x’) => x=x’(разные переходят в разные)

Отображение f сурьективно если Im f =B(каждый переходит в каждый)

Если же отображение инъективно+сурьективно, то множества равномощны(содержат

одинаковое кол-во элементов), а отображение биективно - взаимооднозначно.

Счетные множества - множества равномощные множеству натуральных чисел (N)

Теорема: Множество Q счетно.

Докозательство: Q=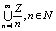

Лемма 1: " nÎN Z/n - счетно.

Каждому элементу из N надо взаимноднозначно сопоставить элемент Z/n:

10®0/n 5®-2/n

2®+1/n 6®+3/n

3®-1/n 7®-3/n

4®+2/n ...

Лемма 2: Объединение счетного или конечного(не более чем счетного) числа

счетных множеств - счетно.

А1={а11, а12, а13,...}

А2={а21, а22, а23,...}

А3={а31, а32, а33,...}

...

Применяем диагональную нумерацию (а11 - 1; а21 - 2; а

12 - 3; а31 - 4; а22 - 5...) и таким образом

взаимнооднозначно сопоставляем каждому элементу из таблицы его номер, значит

объединение счетного или конечного числа счетных множеств - счетно.

Часть может быть равномощна целому: (-1,1) равномощен R (через

полуокружность и лучи)

Из Леммы1 и Леммы 2 получаем: Множество рациональных чисел счетно

2. Определение действительного числа бесконечной десятичной дробью.

Плотность Q в R.

Действительные числа - множество чисел вида [a0],а1

a2 а3... где а0ÎZ а1,а2

,а3,... Î{0,1,...,9}

Действительное число представляется в виде суммы целой и дробной части:

[ао],а1 а2 а3...ак (0) =

ао + а1/10 + а2/100 + ... +ак/10

k = [ао],а1 а2 а3...а’к

(9), где а’к=ак-1

х=[хо],х1 х2 х3...хк...

у=[уо],у1 у2 у3...ук...

х’к - катое приближение икса с недостатком = [хо],х1 х2 х3...хк

у”к - катое приближение игрека с избытком = [уо],у1 у2 у3...ук + 1/10k

х’к+1 > х’к (х’к - монотонно растет)

у”к+1 £ у”k (у”k - не возрастает), т.к. у”к=[уо],у1 у2 у3...ук + 1/10к

у”к+1 = [уо],у1 у2 у3...ук ук+1 + 1/10к+1

у”к - у”к+1 = 1/10к - ук+1 + 1/10к+1 ³ 0

10 - ук+1 - 1 / 10к+1 ³ 0

9 ³ ук+1

Определение: 1) х > у <=> $ к: х’к > у”к

2) х = у <=> х’к не> у”к & у”к не> х’к

По определению получаем, что [1],(0)=[0],(9)

Свойства: 1)" х, у либо х<у, либо х>у, либо х=у

2) х>у & у>z => х>z

3) х не> х

Док-во (2): х>у

у>z

х’к>у”к у’m>z”m

n=max{k;m}

х’n³х’к>у”к³у”n у’n³

у’m>z”m³z”n

у”n>у’n => х’n>z”n

Определение: Если АÌR и " х,уÎR $ аÎА: х<а<у, то А плотно в R

Теорема: Q плотно в R.

Доказательство: х > у х’к > у”к х ³ х’к у”к ³ у

х ³ х’к / 2 + х’к / 2 > х’к / 2 + у”к / 2 > у”к / 2 + у”к / 2 > у

Видим: х > х’к / 2 + у”к / 2 > у, где (х’к / 2 + у”к / 2)ÎQ

3.Несчетность множества действительных чисел.

Теорема: R несчетно.

Доказательство от противного:

1«х1=[х1], х11 х12 х13... |

2«х2=[х2], х21 х22 х23... | Пусть здесь нет девяток в периоде

3«х3=[х3], х31 х32 х33... |

... | (*)

к«хк=[хк ], хк1 хк2 хк3... |

... |

Найдем число которого нет в таблице:

с=[с], с1 с2 с3...

[с]¹[х1] => с¹х1

с1 Ï {9;х21} => с¹х2

с2 Ï {9;х32} => с¹х3

...

ск Ï {9;хк+1к} => с¹хк

Таким образом С - число которое отсутствует в таблице (*)

5.Теорема Дедекинда о полноте R

Пусть 1) 0¹АÍR; 2) " aÎA, " bÎB: а<b; 3) АÈB=R, тогда $! сÎR: " aÎA, " bÎB: а£с£b

Замечания: 1) для Q и I не выполняется (между двумя иррациональными

всегда одно рациональное следует из теоремы о плотности Q в R)

2) А называют нижним множеством сечения (нижний класс), В называют верхним

множеством сечения (верхний класс)

Доказательство:

" aÎA, " bÎB: а<b => A ограничено сверху => $ SupA=m =>

"bÎB: b³m => B ограничено снизу =>$ InfB=n, m£n

Докажем, что m = n:

Пусть m<n, тогда из теоремы о плотности Q в R следует, что $ сÎQ:

m<c<n => cÏА & cÏВ - невозможно по свойству 3 отсюда и

из того, что m£n

следует, что m=n если обозначим m=n через c, то получим а£с£b

Докажем, что с единственное(от противного):

Пусть $с’¹с,с’>с (с’<с), так как c=n=InfB=m=SupA=>по опр-нию.

"с’>с (с’<с) найдется такое b(a), что b<c’ (a>c’)-противоречие с

"aÎA, "bÎB: а£с£b

8.Лемма о зажатой последовательности (Лемма о двух милиционерах)

Если $n0: "n>n0 xN£yN

£zN и $ Lim xN=x, $ Lim zN=z, причем x=z,

то $ Lim yN=y => x=y=z.

Доказательство: "n>n0 xN£yN£zN

Возьмем произвольно Е>0, тогда $ n’: "n>n’ xNÎ(х-Е,х+Е)

& $ n”: "n>n” zNÎ(х-Е,х+Е) => "n>max{n0

,n’,n”} yNÎ(x-E,x+E)

4. Верхние и нижние грани числовых множеств.

Определение: АÌR mÎR, m - верхняя (нижняя) грань А, если " аÎА а£m (а³m).

Определение: Множество A ограничено сверху (снизу), если существует такое

m, что " аÎА, выполняется а£m (а³m).

Определение: SupA=m, если 1) m - верхняя грань A

2) " m’: m’<m => m’ не верхняя грань A

InfA = n, если 1) n - нижняя грань A

2) " n’: n’>n => n’ не нижняя грань A

Определение: SupA=m называется число, такое что: 1) " aÎA a£m

2) "e>0 $ aEÎA, такое, что aE>a-e

InfA = n называется число, такое что: 1) 1) " aÎA a³n

2) "e>0 $ aEÎA, такое, что aE<a+e

Теорема: Любое, непустое ограниченное сверху множество АÌR, имееет

точную верхнюю грань, причем единственную.

Доказательство:

Построим на числовой прямой число m и докажем что это точная верхняя грань А.

[m]=max{[a]:aÎA} [[m],[m]+1]ÇA¹Æ=>[m]+1 - верхняя грань A

Отрезок [[m],[m]+1] - разбиваем на 10 частей

m1=max[10*{a-[m]:aÎA}]

m2=max[100*{a-[m],m1:aÎA}]

...

mк=max[10K*{a-[m],m1...mK-1:aÎA}]

[[m],m1...mK, [m],m1...mK + 1/10

K]ÇA¹Æ=>[m],m1...mK + 1/10

K - верхняя грань A

Докажем, что m=[m],m1...mK - точная верхняя грань и что она единственная:

"к: [m’K,m”K)ÇA¹0; "к "аÎА: а<m”K

Единственность(от противного):

аÎА, пусть а>m”K => $ к: а’K>m”K

=> а³а’K>m”K - это противоречит ограниченности

=> a£m

Точная верхняя грань:

Пусть l<m, тогда $ к: m’K>l”K, но так как "к [m’

K,m”K) ÇA¹0 => $ аÎ[m’K,m”

K) => а>l =>l - не верхняя грань.

Теорема: Любое, непустое ограниченное снизу множество АÌR, имееет

точную нижнюю грань, причем единственную.

Рассмотрим множество B{-а: аÎА}, оно ограничено сверху и не пусто => $ -SupB=InfA

6.Бесконечно малые и бесконечно большие последовательности. Их свойства.

Определение: Последовательность аN называется

бесконечно малой (бм) если ее предел равен нулю ("Е>0 $ n0:

n>n0 |аN|<Е)

Теорема: Сумма (разность) бм последовательностей является бм

последовательностью.

Доказательство: Пусть Lim aN=Lim bN=0, cN=a

N+bN, dN=aN-bN. Так как вне

любой эпсилон-окрестности точки 0 (в частности окрестности Е/2) лежит

конечное число членов последовательности aN, т.е. $ n’:

"n>n’: |aN|<Е/2. Аналогично $ n”: "n>n”: |bN

|<Е/2. При n>max{n’,n”} выполнены оба неравен ства |aN|<Е/2

& |bN|<Е/2 => при любом n> max{n’,n”} имеем: |cN

|=|aN+bN|£|aN|+|bN|<E/2 +

E/2 = E => |dN|=|aN-bN| £ |aN

|+|bN|<E/2 + E/2 = E

Теорема: Произведение бм и ограниченной последовательности - бм

последовательность.

Доказательство: Пусть aN - бм посл-ть, bN - ограниченная посл-ть zN=aN*bN.

Т.к. bN - ограниченная посл-ть, значит $ такое с: |bN|£с¹0

Т.к. aN - бм посл-ть, значит вне любой Е-окрестности точки 0 (в

частности Е/с)лежит конечное число членов посл-ти aN, т.е. $ n0

: "n>n0 |aN|<Е/с.Таким образом "n>n0:

|zN|=|aN*bN|=|aN|*|bN

|<Е/с * с=Е

Следствие: произведение бм посл-тей - тоже бм посл-ть

Теорема: Пусть aN - бм. Если $ n’: "n>n’ последовательностьть |bN|£aN => bN - бм

Доказательство: aN - бм => $ n”: "n>n”: |aN|<Е. Для n>=max{n’,n”} |bN|£|aN|<Е

Определение: Последовательность аN называется бесконечно

большой (бб) если "Е>0 $ n0: n>n0 |аN

|>Е)

Теорема: Если aN - бм, то 1/aN - бб последовательностьть, обратное тоже верно.

Доказательство:

"=>" aN-бм=>вне любой эпсилон-окрестности точки 0 (в частности

1/Е) находится конечное число членов посл-ти, т.е. $n0: "n>n

0 |aN|<1/E =>1/|aN|>Е.

"<=" 1/|aN| - бб последовательность => "Е>0 $ n0: "n>n0 1/|aN|>1/Е => |aN|<Е

Теорема: Пусть aN - бб. Если $ n’: "n>n’ последовательность

bN³|aN| => bN - бб.

Доказательство: aN - бб => $ n”: "n>n” |aN|>Е. Для n>max{n’,n”} bN³|aN|>Е

7.Арифметика пределов

Предложение: Число а является пределом последовательности a

N если разность aN-a является бм (обратное тоже

верно)

Докозательство: Т.к. Lim aN=a, то |aN-a|<Е. Пусть aN=aN-a. |aN|=|aN-a|<Е

Обратное: Пусть aN=aN-a, т.к. aN - бм => |aN|£Е. |aN|=|aN-a|<Е

Теорема: Если Lim xN=x, Lim yN=y, то:

1. $ Lim (xN+yN) и Lim (xN+yN)=х+у

2. $ Lim (xN*yN) и Lim (xN*yN)=х*у

3. "n yN¹0 & y¹0 => $ Lim (xN/yN) и Lim(xN/yN)=х/у

Страницы: 1, 2, 3, 4, 5, 6