|
достигает верхней
граница в точке a. Существование точки b=Inf{f(x):xÎ[a,b]} доказывается
аналогично.
35. Равномерная непрерывность. Ее характеризация в терминах колебаний.
Определение: "Е>0 $ d>0: "х’,х”: |х’-х”|<d =>
|f(x’)-f(x”)|<Е => функция называется равномерно непрерывной
Отличие от непрерывности состоит в том, что там d зависит от Е и от х”, то
здесь d не зависит от х”.
Определение: Ф-ция f - не равномерно непрерывна, если $ Е>0 "d >0:
$ х’,х”: |х’-х”|<d => |f(x’)-f(x”)|³Е>0
Рассмотрим множество , IÍDf.
Верхняя точная граница этого множества обозначаемое Wf(d) называется
колебанием функции f на множестве I вызванное колебаниями аргумента:
1/х - Wf(d) = +¥; Sin x - Wf(d) = 1
Таким образом равномерно непрерывную функцию можно определить по другому:
"Е>0 $ d>0: Wf(d)£Е Lim Wf(d)=0 d®0
36.Теорема Кантора о равномерной непрерывности непрерывной функции на отрезке.
Теорема: Если f непрерывна на [a,b], то она равномерно непрерывна на [a,b].
Доказательство(от противного):
Пусть f не равномерно непрерывна на [a,b]=>$Е>0 "d>0 $х’,х”:
|х’-х”|<d=>|f(x’)-f(x”)|³Е. Возьмем d =1/к, кÎN $хK
, х’KÎ[a,b]: |хK-х’K|<1/к |f(xK
)-f(x’K)|³E
Т.к хK - ограничена => из нее по теореме Больцано-Вейерштрасса
можно выделить подпосл-ть xKs сходящуюся к х0. Получаем:
|хKs-х’Ks|<1/к
хKs-1/k<х’Ks<хKs-1/k по Лемме о зажатой
посл-ти х’Ks®х0 kS®¥ |f(xKs
)-f(x’Ks)|³E кS®¥ => 0³E - противоречие с
условием.
37.Определение производной и дифференциала.
Касательная в точке x0 к функции x®f(x): возьмем еще одну точку х
соединим x0 и х - получим секущую. Касательной назовем предельное
положение секущей при х®x0, если это предельное положение
существует. Т.к. касательная должна пройти ч/з точку (x0,f(x0
) => уравнение этой касательной (если она не вертикальна) имеет вид y=k*(x-x
0)+f(x0). Необходимо только опр-ть наклон k
касательной. Возьмем произвольное число Dх¹0 так, чтобы x0
+DхÎХ. Рассмотрим секущую МОМ, МО(x0,f(x
0)), М(x0+Dх,f(x0+Dх)). Уравнение секущей имеет вид:
у=к(Dх)(х-x0)+f(x0), где k=f((x0+Dх)-f(x0
))/Dх - наклон секущей. Если существует Lim к(Dх) при Dх®0, то в качестве
искомого наклона k возьмем это предел. Если Lim к(Dх)=¥ при Dх®0,
то перепишем уравнение секу щей в виде x=(1/k(Dх))*(y-f(x0))+x0
перейдя к пределам при Dх®0, получим x=x0 (Lim x=Lim x0
Dх®0 => x = Lim x0)
Определение: Производным значением функции f в точке х0
называется число f’(х0)=Lim (f(x0+Dх)-f(x0))/
Dх x®x0, если этот предел существует.
Геометрически f’(х0) - это наклон невертикальной касательной в точке
(x0,f(x0)). Уравнение касательной y=f’(x0
)*(x-x0)+f(x0). Если Lim (f(x0+Dх)-f(x
0))/Dх=¥ Dх®0, то пишут f`(x0)=¥ касательная в этом
случае вертикальна и задается уравнением х=x0. f`(x0
)=lim(f(x0+Dх)-f(x0))/Dх x®x0=>(f(x0
+Dх)-f(x0))/Dх=f’(x0)+a(x), a(x)®0 при x®x0.
f(x0+Dх)-f(x0)=f`(x0)*Dх+a(x)*Dх учитывая, что
x0+Dх=x и обозначая a(x)*Dх через o(x-x0) получим
f(x)=f’(x0)*(x-x0)+f(x0)+o(x-x0).
Необхо димо заметить, что o(x-x0) уменьшается быстрее чем (x-x0
) при x®x0 (т.к. o(x-x0)/(x-x0)®0 при x®x0
)
Определение: Ф-ция f называется дифференцируемой в точке x0
если $сÎR: в некоторой окрестности точки x0 f(x)=С(x-x0
)+f(x0)+o(x-x0)
Теорема: Функция диффференцируема в точке x0 <=> $ f’(x0)
Доказательство:
<=: f(x)=f’(x0)*(x-x0)+f(x0)+o(x-x0) => f`(x0)=C
=>: f(x)=C(x-x0)+f(x0)+o(x-x0) =>
(f(x)-f(x0))/(x-x0)=C+o(x-x0)/(x-x0
)=C+a(x), a(x)®0 при x®x0.
Переходим к пределу при x®x0 => Lim (f(x)-f(x0))/(x-x
0)=C+0=C => Слева записано производное значение ф-ции f => по
определению C=f`(x0)
Определение: Если функция х®f(x) дифференцируема в точке x0,
то линейная функция Dх®f’(x0)*Dх называется дифференциалом функции f
в точке x0 и
обозначается df(x0). (диф-ал ф-ции х®х обозначают dx). Т.о. df(x
0):Dх®f`(x0)*Dх и dх:Dх®Dх. Отсюда df(x0)=f’(x0
)*dх => df(x0)/dх: Dх®f`(x0)*Dх/Dх=f’(x0)
при Dх¹0. В силу этого пишут также f’(x0)=df(x0)/dх
- обозначение Лейбница. График диф-ла получается из графика касательной
переносом начала коор динат в точку касания.
Теорема: Если ф-ция f диф-ма в точке x0, то f непрерывна в точке x0.
Докозательство: f(x)=f(x0)+f’(x0)*(x-x0)+o(x-x
0)®f(x0) при x®x0 => f непрерывна в точке x0
.
Определение: Нормаль к ф-ции f в точке x0: это прямая
перпендикулярная касательной к ф-ции f в точке x0. Учитывая что
тангенс угла наклона нормали равен tg(90+угол наклона касательной)=
-Ctg(наклона касательной), получаем уравнение нормали: y=-1/f’(x0
)*(x-x0)+f(x0)
38. Арифметика диф-цирования. Производные тригонометрических функций.
Теорема: Пусть ф-ции f и g дифференцируемы в точке x0, тогда
ф-ции f+g, f*g и f/g (при g(x0)¹0) дифференцируемы в точке x
0 и:
1) (f+g)’(x0)=f’(x0)+g’(x0)
2) (f*g)’(x0)=f’(x0)*g(x0)+f(x0)*g’(x0)
3) (f/g)’(x0)=(f’(x0)*g(x0)-f(x0)*g’(x0))/g(x0)2
Доказательство:
1) Df(x0)=f(x0+Dx)-f(x0)
Dg(x0)=g(x0+Dx)-g(x0)
D(f+g)(x0)=Df(x0)+Dg(x0)=f(x0+Dx)-f(x0)+g(x0+Dx)-g(x0)
D(f+g)(x0)/Dx=(f(x0+Dx)-f(x0)+g(x0
+Dx)-g(x0))/Dx=(f(x0+Dx)-f(x0))/Dx+(g(x0
+Dx)-g(x0))/Dx®f’(x0)+g’(x0) при Dx®0
2) D(f*g)(x0)=f(x0+Dx)*g(x0+Dx)-f(x0
)*g(x0)=(f(x0)+Df(x0))*(g(x0)+D(x
0))-f(x0)*g(x0)=g(x0)*Df(x0
)+f(x0)*Dg(x0)+Df(x0)*Dg(x0)
D(f*g)(x0)/Dx=g(x0)*(Df(x0)/Dx)+f(x0
)*(Dg(x0)/Dx)+(Df(x0)/Dx)*(Dg(x0)/Dx)*Dx®f’(x
0)*g(x0)+f(x0)*g’(x0) при Dx®0
3) Ф-ция g - дифференцируема в точке x0 => Ф-ция g - непрерывна в
точке x0 => "Е>0 (Е=|g(x0)|/2) $d>0: |Dx|< d
=> |g(x0+Dx)-g(x0)|<|g(x0)|/2.
g(x0)-|g(x0)|/2<g(x0+Dx)<g(x0
)+|g(x0)|/2. Рассматривая функцию g при таких x (|Dx|<d) видим что
g(x0+Dx)¹0.
Рассмотрим разность (1/g(x0+Dx)-1/g(x0))/ Dx = -(g(x0
+Dx)-g(x0))/Dx*g(x0+Dx)*g(x0) ® -g’(x0
)/g(x0)2 при Dx®0
(f/g)’(x0)=(f*1/g)’(x0) => (2) = f’(x0
)*1/g(x0)+f(x0)*(1/g)’(x0)=f`(x0
)*1/g(x0)+f(x0)*(-g’(x0)/g(x0)2
)=(f’(x0)*g(x0)-f(x0)*g’(x0))/g(x
0)2
Теорема: Пусть f=Sin(x), g=Cos(x)
1) Sin’(x0) = Cos (x0)
2) Cos’(x0) = -Sin (x0)
Доказательство:
1) Df/Dx=(Sin(x0+Dx)-Sin(x0))/Dx = Sin(Dx/2)/(Dx/2) *
Cos(x0+Dx/2) ® Сos x0 при Dx®0
2) Dg/Dx=(Cos(x0+Dx)-cos(x0))/Dx=Sin(Dx/2)/(Dx/2)*-Sin(x
0+Dx/2) ® -Sin x0 при Dx®0
Производные Tg и Ctg выводятся непосредственно из производных для Sin и Cos
по формулам дифференцирования.
39. Производная суперпозиции.Производные степенной, показательной и
логарифмической функции.
Теорема: Пусть функция g диф-ма в точке x0, а ф-ция f диф-ма в
точке y0=g(x0), тогда ф-ция h(х)=f(g(х)) диф-ма в точке x
0 и h’(x0)=f`(y0)*g’(x0)
Доказательство:
Dy=y-y0, Dx=x-x0, Df(y0)=f’(y0)*Dy+o(Dy), Dg(xo)=g’(xo)*Dx+o(Dx), y=g(x0+Dx)
Dh(x0)=f(g(x0+Dx))-f(g(x0))=f(y)-f(y0
)=f’(y0)*Dy+o(Dy)=f’(y0)*(g(x0+Dx)-g(x0
))+o(Dg)==f’(y0)*(g’(x0)*Dx+o(Dx))+o(Dy)= f’(y0
)*g’(x0)*Dx+f’(y0)*o(Dx)+o(Dy)
Dh(x0)/Dx=f’(y0)*g’(x0)+r, r=f`(y0)*o(Dx)/Dx+o(Dy)/Dx
r=f`(y0)*o(Dx)/Dx+o(Dy)/Dx=f`(y0
)*(a(x)*Dx)/Dx+(a’(x)*Dy)/Dx=f’(y0)*a(x)+a’(x)*Dy/Dx®f’(y0
)*0 + 0*g’(y0) при Dx®0 (a(x)®0 a’(x)®0)
Производная:
1) xa=a*xa-1
Lim (Dy/Dx)=lim((x+Dx)a-xa)/Dx = Lim xa-1*
((1+Dx/x)a-1)/Dx/x. Используя замечательный предел x®0 Lim ((1+x)
a-1)/x=a, получим Dx®0
Lim xa-1*Lim((1+Dx/x)a-1)/Dx/x = a*xa-1
2) (aX)’=aX*Ln a (x®aX)’=(x®eX*Ln a)’
x®eX*Ln a - композиция функций x®еX и x®x*Ln a обе
непрерывны на R => (x®aX)’=(x®е X*Ln a)’=(x®еX
*Ln a)’*(x®x*Ln a)’=aX*Ln a
Д-во : (eX)’=eX
Lim(Dy/Dx)=Lim(eX+DX-eX)/Dx=Lime
X*(eDX-1)/Dx, используя зам-ный предел при x®0 Lim(e
X-1)/x=1, получим при Dx®0 Lim(Dy/Dx)=eX
3) (LogA(x))’=1/x*Ln a
Lim(Dy/Dx) = Lim (LogA(x+Dx) - LogA(x))/Dx = Lim 1/x*Log
A(1+Dx/x)/Dx/x, используя замечательный предел при x®0 Lim LogA
(1+x)/x=1/Ln a, получим
Lim (Dy/Dx) = Lim 1/x*Lim LogA(1+Dx/x)/Dx/x=1/x*Ln a
40. Производная обратной функции. Производные обратных тригонометрических
функций.
Предложение: Если производная обратной функции g для ф-ции f существует в
точке y0, то g’(y0)=1/f’(x0), где y0
=f(x0)
Доказательство: g(f(x))=x g’(f(x))=1
g’(f(x0))=g’(f(x0))*f’(x0)=1, g’(f(x0))=g(y0)=1/f’(x0)
Теорема: Пусть ф-ция f строго монотонно и непрерывно отображает (a,b) в
(а,b) тогда $ обратная ей ф-ция g, которая строго монотонно и непрерывно
отображает (а,b) в (a,b). Если f диф-ма в точке x0Î(a,b) и
f’(x0)¹0, то g диф-ма в точке y0=f(x0) и
g’(y0)=1/f’(x0)
Доказательство:
Возьмем произвольную последовательность сходящуюся к y0: yN
®y0, yN¹y0 => $ посл-ть xN:
xN=g(yN), f(xN)=yN
g(yN)-g(y0)/yN-yO = xN-x
O/f(yN)-f(yO) = 1/f(yN)-f(yO
)/xN-xO ® 1/f’(xo) при n®¥, получили при xN
®xO g(yN)-g(yO)/yN-yO
®1/f’(xO) => g’(уO)=1/f’(xO)
Производные:
1) x®Arcsin x по теореме имеем Arcsin’x=1/Sin’y, где Sin y=x при условии, что
Sin’y<0, получаем (используя производную синуса): Arcsin’x=1/Cos y, т.к.
Arcsin: [-1,1]®[-П/2,П/2] и Cos:[-П/2,П/2]®[0,1], то Cos y³0 и, значит
Arcsin’x = 1/Cos y = 1/(1-Sin2y)1/2 = 1/(1-x2)
1/2
2) x®Arccos’x = -1/(1-x2)1/2
3) x®Arctg’x = 1/1+x2
4) x®Arcctg’x= -1/1+x2
41.Производные и дифференциалы высших порядков.
Определение: Если ф-ция f диф-ма в некоторой окрестности точки xO
, то ф-ция f’(x):x®f’(x) в свою очередь может оказаться диф-мой в точке xO
или даже в некоторой ее окрестности. Производная ф-ции f’(x) - называется
второй производной (или производной порядка 2) ф-ции f в точке xO и
обознача ется f”(x). Аналогично определяется третья и четвертая производная и
так далее. Для единообразия обозначаем через fN(xO) -
производную порядка n функции f в точке xO и при n=0 считаем f0
(xO)=f(xO).
Замечание: Cуществование производной порядка n требует того чтобы
существовала производная пордка (n-1) уже в некоторой окрестности точки xO
(следует из теоремы о связи диф-ти и непрерывности), в таком случае функция x®f
N-1(x) непрерывна в точке xO, а при n³2 все производные
порядка не выше (n-2) непрерывны в некоторой окрестности точки xO.
Определение: Дифференциалом ф-ции f порядка n в точке xO
называют функцию dх®fN(x)*dх и обозначают dNf(x). Таким
образом dNf(x):dх®fN(x)dxN.
Так как fN(x)dхN:dх®fN(x)dxN, то d
Nf(x)=fN(x)dхN. В силу этого соотношения производную fN
(x) обозначают также dNf(x)/dхN
Инвариантность:
Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную функцию
у=f(g(t)). Если существуют производные у’(х) и х’(t) то cуществует производная
у’(t)=у’(х)*х’(t). Если х считать независимой переменной, то диф-ал dy=y’(х)dx.
Перейдем к независимой переменной t, учитывая что у’(t)=у’(х)*х’(t):
dy=y’(t)dt=y’(x)*х’(t)dt. x’(t)dt=dх => dy=y’(t)dt=у’(х)*х’(t)*dt=у’(x)dх -
видим что при переходе к новой независимой переменной форма дифференциала может
быть сохранена - это свойство называют инвариантностью формы первого
дифференциала.
Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную функцию
у=f(g(t)) Если существуют производные у’(х) и х’(t) то существует производная
у’(t)=у’(х)*х’(t) и по доказанному ее первый диф-ал по t можно написать в форме
dy=y’(х)dх, где dх=x’(t)dt. Вычисляем второй диф-ал по t: d2
y=d(y’(x)dx)=dy’(x)dx+y’(x)d(dx). Снова пользуясь инвариантностью первого диф-ла
dy’(x)=у”(х2)dx => d2y=у”(х2)dx2
x+y’(x)*d2x, в то время как при независимой переменной х второй
диф-ал имел вид д2y=у’(х2)*dx2x =>
неинвариантность формы второго диф-ла.
Формула Лейбница:
f(x)=u(x)*v(x) 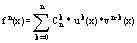
Доказательство по индукции.
1) n=0 верно
2) Предположим для n - верно => докажем для (n+1)
Если для u и v $(n+1) производные, то можно еще раз продифференцировать по х
- получим:
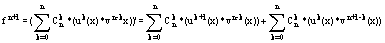
Объединим теперь слагаемые обеих последних сумм, содержащие одинаковые
произведения производных функций u и v (сумма порядков производ ных в таком
произведении, как легко видеть, равна всегда (n+1)). Произведение u0
*vN+1 входит только во вторую сумму с коэффициентом С0
N=1. Произведение uN+1*v0 входит только в первую
сумму с коэффициентом СNN=1. Все остальные произведения
входящие в эти суммы имеют вид uK*vN+1-K. Каждое такое
произведение встречается в первой сумме с номером k = i-1, а во второй i=k.
Сумма соотв. коэффициентов будет 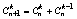
=>
получаем fN+1(x)=u0*vN+1+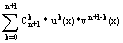 + uN+1*v0= + uN+1*v0=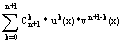
44. Нахождение промежутков постоянства монотонности функции и ее экстремумов.
Теорема: Пусть f(x) непрерывна в замкнутом промежутке [a;b] и диф-ма в
открытом промежутке (a;b), если f’(x)=0 в (a;b), то f(x)-const в [a;b].
Докозательство:
Пусть x£b, тогда в замкнутом промежутке в [a;x] по теореме Лагранжа имеем:
f(x)-f(a)=f’(a+q(x-a))(x-a) 0<q<1 => т.к. по условию f’(x)=0 в (a;b),
то f’(a+q(x-a))=0 => f(x)=f(a)=Const для все хÎ(a;b).
Теорема: Пусть f(x) непрерывна в замкнутом промежутке [a;b] и диф-ма в
открытом промежутке (a;b), тогда:
1) f монотонно возрастает(убывает) в нестрогом смысле в (a;b) <=>
f’(x)³0(f’(x)£0) в (a;b).
2) Если f’(x)>0(f’(x)<0) в (a;b) и f непрерывна в [a;b], то f строго
возрастает(убывает) в [a;b].
Доказательство:
1) Пусть f непрерывна на [x’,x”] x’, x”Î(a;b), тогда по теореме Лагранжа
(f(x”)-f(x’))/(x”-x’)=f’(c), сÎ(x’,x”). По условию имеем
f’(x)³0(f’(x)£ 0) в (a;b) => f’(c)³0(f’(c)£ 0) =>
f(x”)³f(x’)( f(x”)£f(x’)) => f(x) возрастает(убывает) в нестрогом
смысле в (a;b).
2) Используя аналогичные (1) рассуждения, но заменяя неравенства на строгие
получим (2).
Следствие: Если xO-критическая точка непрерывной ф-ции f.
f’(x) в достаточно малой d-окр-ти точки xO имеет разные знаки, то x
O-экстремальная точка.
Достаточное условие экстремума: (+)®xO®(-) => локальный min, (-)®x
O®(+) => локальный max
46. Выпуклые множества Rn. Условие Иенсена. Выпуклые функции.Неравенство
Йенсена.
Определение: Множество М выпукло <=> если " А,ВÎМ [А,В]ÌМ
[А,В]ÌМ => [А,В]={А+t(В-А):tÎ[0,1]} => А(1-t)+tВÎМ
[А,В]ÌМ => А,ВÎМ; l1=1-t, l2=t => l1+l2=1 l1,l2³0 => l1А+l2ВÎМ
Рассмотрим точки: А1,А2,...АNÎМ l1,l2³0 S(i=1,n): lI = 1
Докажем что S(i=1,n): lI*АI ÎМ
Д-во: По индукции:
1) n=1, n=2 - верно
2) Пусть для (n-1) - верно => докажем для n:
а) lN=1 => приравниваем l1=...=l N-1=0 => верно
б) lN<1 l1*А1 +...+ lN-1*А
N-1 + l N*А N= (1-l N)((l1
/1-l N)*А1+...+(lN-1/1-l N)*А
N-1) + l N*А N = (1-l N)*B + l N
*А N
BÎМ - по индуктивному предположению А NÎМ - по условию=>(1-l N)*B + l N*А N ÎМ Ч.т.д
График Гf = {(x,f(x)):хÎDf}, Надграфик UPf={(x,y):y>f(x)}
Определение: Функция f выпукла <=> UPf - множество выпукло.
Условие Йенсена: АIÎМ lI³0 S(i=1,n): l
I =1 => S(i=1,n): lI*АI ÎМ, xI
³0, f(xI)£yI => S(i=1,n): lI*А
I = (SlI*xI;SlI*yI) => f(Sl
I*xI)£SlI*yI
Неравенство Йенсена: АIÎМ lI³0 SlI =1f(SlI*xI)£SlI*f(xI)
47.Критерий выпуклости дифференцируемой функции.
Теорема: Пусть f определена в интервале (a;b), тогда следующие условия
эквивалентны: 1) f - выпукла в (a;b) ~ 2) "x’,xO
,x”Î(a;b) x’<xO<x” =>
(f(xO)-f(x’))/(xO-x’)£(f(x”)-f(xO))/(x”-x
O). Геометрический смысл: при сдвиге вправо угловой коэффициент секущей
растет.
Доказательство:
“=>” AB: k=(y-f(x’))/(xO-x’)³(f(xO)-f(x’))/(x
O-x’) => y³f(xO); AB: k=(f(x”)-y)/(x”-xO
)£(f(x”)-f(xO))/(x”-xO) =>y£f(xO
)
(f(xO)-f(x’))/(xO-x’)£(f(x”)-f(xO))/(x”-xO)
“<=”
Страницы: 1, 2, 3, 4, 5, 6
| 


