Доказательство:

Пусть xN=х+aN, aN - бм; yN=у+bN, bN - бм

1) (xN+yN)-(х+у)=aN+bN (По теореме о

сумме бм: aN+bN - бм => (xN+yn

)-(х+у)-бм, дальше по предложению)

2) xN*yN - х*у = х*aN+у*bN+aN

*bN (По теоремам о сумме бм посл-тей и * бм посл-тей на огр. посл-ти

получаем: xN*yN - х*у - бм, дальше по предл-нию)

3) xN/yN - х/у = (у*aN-х*bN) /

(у*(у+bN))= (у*aN-х*bN) * 1/у * 1/уN

доказательство сводится к доказательству утверждения: если уn -

сходящаяся не к 0 посл-ть, то 1/уN тоже сходящаяся

последовательность: Lim уN=y => по определению предела получаем $

n0: "n>n0 |уn-у|<у/2 (Е=y/2), что равносильно

неравенству: у-у/2<уN<у/2+у, откуда получаем: |уN

|³уN>у/2.|уN|>у/2=>1/|уN|<2/у

=> "n: 1/|уN|£max{2/у, 1/у1, 1/у2

,...1/уno}

Теорема: Если хN сходится к х, yN сходится к у и $

n0: "n>n0 последовательность хN£у

N, то х£у

Доказательство(от противного): Пусть х>у. Из опр. предела "E>0 (в

частности Е<(у-х)/2): $n’: "n>n’ |xN-x|<E и $n”: "n>n”

|yN-y|<E. Получаем "n>max{n’,n”} все члены посл-ти xN

будут лежать в Е-окрестности точки х, а все члены посл-ти уN будут

лежать в Е-окрестности точки у, причем

(х-Е,х+Е)Ç(у-Е,у+Е)=Æ. И т.к мы предположили, что х>у, то

"n>max{n’,n”}: хN>уN - противоречие с условием

=> х£у.

5. Определение предела последовательности и его единственность.

Определение: Пусть даны два множества Х и У. Если каждому элементу

хÎХ сопоставлен по определенному правилу некоторый элемент уÎУ, то

говорят, что на множестве Х определена функция f и пишут f:Х®У или х® (f(х)|

хÎХ).

Определение: Последовательность-это ф-ция определенная на мн-ве N, со

значениями во мн-ве R f:N®R. Значение такой ф-ции в (.) nÎN обозначают а

N.

Способы задания:

1) Аналитический: Формула общего члена

2) Рекуррентный: (возвратная) формула: Любой член последовательности начиная с

некоторого выражаетс через предидущие. При этом способе задани обычно указывают

первый член (или нсколько начальных членов) и формулу, позволющкю определить

любой член последовательности через предидущие. Пример: а1=а; а

N+1=аN + а

3) Словесный: задание последовательности описанием: Пример: аN = n-ый

десятичный знак числа Пи

Определение: Число а называется пределом последовательности а

N, если "e>0 $ n0: "n>n0 выполняется

неравенство |аN-a|<e. Обозначение Lim aN=a.

Если не существует числа а, являющегося пределом посл-ти, то говорят что

последовательность расходится, если существует, то сходится (к числу а

).

Геометрически существование предела последовательности означает, что любой

интервал вида (а-e,а+e), называемый эпсилон-окрестностью точки а,

содержит все члены последовательности аN начиная с

некоторого номера, или что то же самое, вне любой эпсилон-окрестности точки

а находится ко нечное число членов последовательности аN.

Определение: Число а назывется пределом посл-ти аN

если вне всякой окрестности точки а содержится конечное число членов

последова тельности.

Теорема: Сходящаяся последовательность имеет только один предел.

Доказательство(от противного):

Пусть последовательность аN имеет предел а и предел

с, причем а¹с. Выберем такой эпсилон, чтобы пересечение

эпсилон-окрестностей точек а и с бы ло пусто. Очевидно

достаточно взять эпсилон меньше |а-с|/2. Вне окрестности точки а

содержится конечное число членов последовательности => в ок рестности

точки с содержится конечное число членов последовательности - противоречие с

условием того, что с - предел последовательности.

Теорема: Сходящаяся последовательность ограничена.

Доказательство:

Пусть последовательность аN сходится к числу а.

Возьмем какое-либо эпсилон, вне эпсилон-окрестности точки а лежит конечное

число членов последо вательности, значит всегда можно раздвинуть окрестность

так, чтобы все члены последовательности в нее попали, а это и означает что

последователь ность ограничена.

Замечания: 1) Обратное не верно (аn=(-1)N, ограничена но не сходится)

2) Если существует предел последовательности аN, то при

отбрасывании или добавлении конечного числа членов предел не меняется.

Порядковые свойства пределов:

Теорема о предельном переходе: Если Lim xN=x, Lim yN=y, $n0: "n>n0 хN£yN, тогда x£y

Доказательство(от противного):

Пусть х>у => по определению предела $ n0’: "n>n0’

|хN-х|<E(берем Е<|х-у|/2): & $ n0”: "n>n

0” |yN-y|<E. "n>max{n0’, n0”}: |х

N-х|<|х-у|/2 & |уN-у|<|х-у|/2, т.е. получаем 2

интервала (у-Е,у+Е) & (х-Е,х+Е)], причем

(у-Е,у+Е)Ç(х-Е,х+Е)=Æ. "n>max{n0’, n0”} х

NÎ(х-Е,х+Е) & уNÎ(у-Е,у+Е) учитывая, что х>у

получаем: "n>max{n0’, n0”} хN>yN

- противоречие с условием.

Теорема: Если $n0: "n>n0 aN£b

N£cN и $ Lim aN=a, $ Lim cN=c,

причем a=c, то $ Lim bN=b => a=b=c.

Доказательство: Возьмем произвольно Е>0, тогда $ n’: "n>n’ => cN

<(a+E) & $ n”: "n>n” => (a-E)<aN. При n>max{n

0,n’,n”} (a-E)<aN£bN£cN

<(a+E), т.е. " n>max{n0,n’,n”}=>bN

Î(a-E,a+E)

9. Предел монотонной последовательности

Определение: Последовательность называется монотонно возрастающей

(убывающей) если " n1>n2 (n1<n2

): xN1³xN2 (xN1£xN2).

Замечание: Если xN1 строго больше (меньше) xN2,

тогда посл-ть называется строго монотонно возрастающая (убывающая) в случае

нестрогости неравенства последовательность называется нестрого возрастающей

(убывающей).

Теорема: Всякая ограниченная монотонная последовательность сходится.

Доказательство: Пусть хN ограниченная монотонно возрастающая

последовательность. Х={xN: nÎN}

По теореме о существовании точной верхней грани у ограниченного множества имеем:

$ SupX=x, "Е>0 $xE: (х-Е)<хE => $ n0

xNo>(х-E). Из монотон ности имеем: "n>n0 xN

³xNo>(x-E), получили xN£x=SupX, значит

"n>n0 xNÎ(x-E,х]<(x-E,x+E)

10.Лемма о вложенных промежутках

Определение: Пусть а,bÎR и а<b. Числовые множества вида 1-5 -

называются числовыми промежутками:

1) Mножество хÎR: а£х£b (а<х<b) - называется отрезком (интервалом)

2) Mножество хÎR: а£х<b (а<х£b) - открытый справа (слева) промежуток

3) Mножество хÎR: а<х & x<b - открытый числовой луч

4) Mножество хÎR: а£х & х£b - числовой луч

5) Mножество хÎR - числовая прямая

Определение: Число b и а (если они существуют) называются правым и левым

концами отрезка (далее промежутка), и его длина равна b-a

Лемма: Пусть aN монотонно возрастает, bN монотонно

убывает, "n aN£bN и (bN-aN

)-бм, тогда $! с: "n cÎ[aN,bN] (с Ç[aN

,bN])

Доказательство:

aN£bN£b1 aN монтонно возрастает & aN£b1 => $ Lim aN=a

a1£aN£bN bN монтонно убывает & a1£bN => $ Lim bN=b

aN£a b£bN aN£bN => a£b

Lim (bN-aN)=b-a=0(по условию)=>a=b

Пусть c=a=b, тогда aN£c£bN

Пусть с не единственное: aN£c’£bN, с’¹с

aN£c£bN=>-bN£-c£-a

N => aN-bN£c’-c£bN-aN

=> (По теореме о предельном переходе) => Lim(aN-bN

)£Lim(c’-c)£Lim(bN-aN) =>

(a-b)£Lim(c`-c)£(b-a) =>

0£lim(c`-c)£0 => 0£(c`-c)£0 => c’=c => c - единственное.

Перефразировка Леммы: Пусть имеется бесконечнаz посл-ть вложенных друг в

друга промежутков (промежуток 1 вложен в промежуток 2 если все точки промежутка

1 принадлежат промежутку 2: [a1,b1],[a2,b2],...,[an,bn]..., так что каждый

последующий содержится в предыдущем, причем длины этих промежутков стремятся к

0 при n®¥ lim(bN-aN)=0, тогда концы промежутков a

N и bN стремятся к общему пределу с (с разных сторон).

42.Локальный экстремум. Теорема Ферма и ее приложение к нахождению

Определение: Пусть задан промежуток I=(a;b), точка x0

Î(a;b). Точка x0, называется точкой локалниого min(max), если

для всех xÎ(a;b), выполняется

f(x0)<f(x) (f(x0)>f(x)).

Лемма: Пусть функция f(x) имеет конечную производную в точке x0

. Если эта производная f‘(x0)>0(f‘(x0)<0), то для

значений х, достаточно близких к x0 справа, будет f(x)>f(x0

) (f(x)<f(x0)), а для значений x, достаточно близких слева, будет

f(x)<f(x0) (f(x)>f(x0)).

Доказательство: По определению производной,.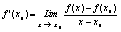

Если f‘(x0)>0, то найдется такая окрестность (x0-d,x

0+d) точки x0, в которой (при х¹x0) (f(x)-f(x

0))/(x-x0)>0. Пусть x0<x<x+d, так что х-х

0>0 => из предыдущего неравенства следует, что f(x)-f(x0

)>0, т.е. f(x)>f(x0). Если же x-d<x<x0 и х-х

0<0, то очевидно и f(x)-f(x0)<0, т.е. f(x)<f(x0

). Ч.т.д.

Теорема Ферма: Пусть функция f(x) определена в некотором промежутке

I=(a;b) и во внутренней точке x0 этого промежутка принимает

наибольшее (наименьшее) значение. Если функция f(x) дифференцируема в точке x

0, то необходимо f‘(x0)=0.

Доказательство: Пусть для определенности f(x) принимает наибольшее значение в

точке x0. Предположение, что f‘(x0)¹0, приводит к

противоречию: либо f‘(x0)>0, и тогда (по лемме) f(x)>f(x0

), если x>x0 и достаточно близко к x0, либо f‘(x0

)<0, и тогда f(x)>f(x0), если x<x0 и достаточно

близко к x0. В обоих случаях f(x0) не может быть

наибольшим значением функции f(x) в промежутке I=(a;b) => получили

противоречие => теорема доказана.

Следствие: Если существует наибольшее (наименьшее) значение функции на

[a;b] то оно достигается либо на концах промежутка, либо в точках, где

производной нет, либо она равна нулю.

43.Теоремы Ролля, Лагранжа, Коши (о среднем значении).

Теорема Ролля

Пусть 1) f(x) определена и непрерывна в замкнутом промежутке [a;b]

2) сущестует конечная производная f’(x), по крайней мере в отткрытом

промежутке (a;b)

3) на концах промежутка функция принимает равные значения: f(a)=f(b)

Тогда между a и b найдется такая точка c(a<c<b), что f’(с)=0.

Доказательство: f(x) непрерывна в замкнутом промежутке [a;b] и потому, по

второй теореме Вейерштрасса (Если f(x), определена и непрерывна в замкну том

промежутке [a;b], то она достигает в этом промежутке своих точных верхней и

нижней границ), принимает в этом промежутке как свое наибольшее значение M,

так и свое наименьшее значение m.

Рассмотрим два случая:

1) M=m. Тогда f(x) в промежутке [a;b] сохраняет постоянное значение: неравенство

m£f(x)£M в этом случае "x дает f(x)=M => f’(x)=0 во всем

промежутке, так что в качестве с можно взять любую точку из (a;b).

2) M>m. По второй теореме Вейерштрасса оба эти значения функцией достигаются,

но, так как f(a)=f(b), то хоть одно из них достигается в некоторой точ ке с

между a и b. В таком случае из теоремы Ферма (Пусть функция f(x)

определена в некотором промежутке I=(a;b) и во внутренней точке x0

этого промежутка принимает наибольшее (наименьшее) значение. Если функция f(x)

дифференцируема в точке x0, то необходимо f‘(x0)=0)

следует, что произ водная f’(с) в этой точке обращается в нуль.

Теорема Коши:

Пусть 1) f(x) и g(x) непрерывны в замкнутом промежутке [a;b] & g(b)¹g(a)

2) сущестуют конечные производные f’(x) и g’(x), по крайней мере в отткрытом

промежутке (a;b)

3) g’(x)¹0 в отткрытом промежутке (a;b)

Тогда между a и b найдется такая точка c(a<c<b), что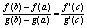

Доказательство: Рассмотрим вспомогательную функцию h(x)=[f(x) - f(a) -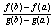

Страницы: 1, 2, 3, 4, 5, 6