|
*(g(x) - g(a))]
Эта функция удовлетворяет всем условиям теоремы Ролля:
1) h(x) непрерывна на [a;b], как комбинация непрерывных функций
2) сущестует конечная производная h’(x) в (a;b), которая равна h’(x)=f’(x) -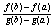
*g’(x)
3) прямой подстановкой убеждаемся h(a)=h(b)=0
Вследствие этого в промежутке (a;b) существует такая точка с, что
h’(x)=0 => f’(c) -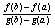
*g’(c) или f’(c) =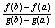
*g’(c).
Разделив обе части равенства на g’(x) (g’(x)¹0) получаем требуемое
равенство.
Теорема Лагранжа:
Пусть 1) f(x) определена и непрерывна в замкнутом промежутке [a;b]
2) сущестует конечная производная f’(x), по крайней мере в отткрытом
промежутке (a;b)
Тогда между a и b найдется такая точка c(a<c<b), что 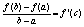
Доказательство: По теореме Коши, полагая g(x)=x, имеем: 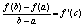
Промежуточное значение с удобно записывать в виде с=а+q(b-a), где
qÎ(0;1). Тогда принимая x0=a, (b-a)=h, мы получаем следующее
следствие:
Следствие: Пусть f(x) дифференцируема в интервале I=(a;b), x0
ÎI, x0+hÎI, тогда $ qÎ(0;1): f(x0+h)-f(x
0)=f’(x0+qh)*h ([x0;x0+h] h>0, [x
0+h;x0] h<0)
11. Подпоследовательности. Теорема Больцано-Вейерштрасса.
Определение: Пусть аN некоторая числовая посл-ть и kN
-строго возрастающая посл-ть N чисел. В результате композиции ф-ций n®aN
и n®kN получа ем посл-ть aKn-которая наз. подпосл-тью
посл-ти aN=>подпосл-сть - это либо сама посл-ть либо исходная
посл-ть, из которой выбросили часть членов.
Теорема: Если Lim аN=а, то и Lim аKn=а.
Доказательство: Вне любой Е-окрестности точки а лежит конечное число
членов последовательности аn и в частности последовательности.
Доказательство: Пусть для заданного Е нашлось n0: "n>n0
|аN-а|<Е, ввиду того что kN®¥ существует и такое
n’, что при всех n>n’ kN>n0 тогда при тех же
значениях n будет верно |аKn-а|<Е
Теорема Больцано-Вейерштрасса: Из всякой ограниченной последовательности
можно выделить сходящуюся подпоследовательность.
Доказательство: хN - ограничена => "n: а£хN
£b. Поделим промежуток [a,b] пополам, хотя бы в одной его половине
содержится бесконечное множество членов посл-ти хN (в противном
случае и во всем промежутке содержится конечное число членов посл-ти, что
невозможно). Пусть [а1,b1] - та половиа, которая
содержит бесконечное число членов посл-ти. Аналогично выделим на промежутке [а
1,b1] промежуток [а2,b2] также содержащий
бесконечное число членов посл-ти хN. Продолжая процесс до
бесконечности на к-том шаге выделим промежуток [аK,bK
]-также содержащий содержащий бесконеч ное число членов посл-ти хN.
Длина к-того промежутка равна bK-аK = (b-a)/2
K, кроме того она стремится к 0 при к®¥ и аK³аK+1
& bK£bK+1. Отсюда по лемме о вложенных
промежутках $! с: "n аN£c£bN.
Теперь построим подпоследовательность:
хN1 Î[а1,b1]
хN2 Î[а2,b2] n2>n1
. . .
хNKÎ[аK,bK] nK>nK-1
а£хNk£b. (Lim aK=LimbK=c из леммы о вложенных промежутках)
Отсюда по лемме о зажатой последовательности Lim хNk=c - ч.т.д.
12.Верхний и нижний пределы последовательности.
xN - ограниченная последовательность =>"n аN£хN£bN
хNK®х, так как хNK-подпоследовательность => "n а£хN£b =>а£х£b
х - частичный предел последовательности хN
Пусть М - множество всех частичных пределов.
Множество М ограничено (а£М£b) => $ SupM & $ InfM
Верхним пределом посл-ти xN называют SupM¹Sup{xN}: пишут Lim xN
Нижним предел ом посл-ти xn называют InfM¹Inf{xN}: пишут lim xN
Cуществование нижнего и верхнего пределов вытекает из определения.
Достижимость:
Теорема: Если хN ограничена сверху (снизу), то $ подпосл-ть х
NK: предел которой равен верхнему (нижнему) пределу хN.
Доказательство: Пусть х=SupM=верхний предел хN
$ х’ÎМ: х-1/к<х’ (следует из того что х - SupМ), т.к. х’ÎМ =>
$ подпоследовательность хNS®х’ => "Е>0 (в частности Е=1/к)
$ s0: "s>s0 =>
х’-1/к<хNS<х’+1/к
х -1/к-1/к<х’-1/к<хNS<х’+1/к<х+1/к (т.к.х-1/к<х’ и х’<х=SupМ)
х-2/к<хNS<х+1/к
Берем к=1: х-2<хNS<х+1, т.е $ s0: "s>s0
это неравенство выполняется берем член посл-ти хNS с номером больше s
0 и нумеруем его хN1
k=1: х-2/1<хN1<х+1/1
k=2: х-2/2<хN2<х+1/2 n1<n2
...
k=k: х-2/к<хNK<х+1/к nK-1<nK
При к®¥ хNK®х
13.Фундаментальные последовательности.
Определение: Последовательность {аN} - называется
фундаментальной, если "Е>0 $ n0: "n>n0 и любого
рÎN выполнено неравенство |аN+р-аN|<Е.
Геометрически это означает что "Е>0 $ n0, такой что расстояние
между любыми двумя членами посл-ти, с большими чем n0 номерами,
меньше Е.
Критерий Коши сходимости посл-ти: Для того, чтобы данная посл-ть
сходилась необходимо и достаточно, чтобы она являлась фундаментальной.
Доказательство:
Необходимость: Пусть Lim xN=x, тогда "Е>0 $ n0: "n>n
0 |хN-х|<Е/2. n>n0, n’>n0 |х
N-хN’|=|хN-х+х-хN’|<|хN
-х|+|х-хN’|<Е/2+Е/2<Е
Достаточность: Пусть хN - фундаментальная
1) Докажем что хN ограничена: Е1=1998 $ n0: |хN-хN’|<Е, n>n0, n’>n0
"n>n0 |хN-хN0|<Е1 х N0-1998<хN<х N0+1998 => хN - ограничена
2) По теореме Больцано-Вейерштрасса
$ подпосл-ть хNK®х. Можно выбрать к настолько большим, чтобы
|хNK-х|<Е/2 и одновременно nк>n0.
Следовательно (из фунд-ти) |хN-хNK|<Е/2 =>
|хNK-х|<Е/2 => х-Е/2<хNK<х+Е/2 => |хN-хNK|<Е/2 => хNK-Е/2<хN<хNK+Е/2 => х-Е<хN<х+Е => |хN-х|<Е
14.Бином Ньютона для натурального показателя.Треугольник Паскаля.
Формула Ньютона для бинома:
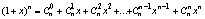 nÎN nÎN
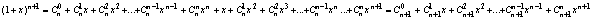
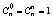
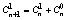 Разложение Паскаля Разложение Паскаля
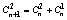 (Записав коэффициенты в виде пирамиды - получим треугольник Паскаля) (Записав коэффициенты в виде пирамиды - получим треугольник Паскаля)
...
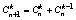
*: 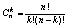 к=0,1,...,n к=0,1,...,n
Доказательство(по индукции):
1) n=0 - верно (1+х)0=1 =>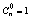 (1+х)0 = (1+х)0 =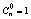
2) Пусть верно для n: докажем что это верно и для n+1:
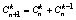 = =
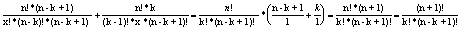
Ч.т.д
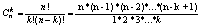
16.Последовательности 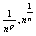 (во всех пределах n®¥) (во всех пределах n®¥)
1) Lim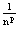 = 0 (p>0) = 0 (p>0)
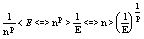 - это означает что, мы нашли такое n0= - это означает что, мы нашли такое n0=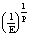 : "n>n0 | : "n>n0 |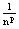 |<E |<E
2) Lim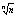 =1 =1
xN=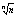 - 1 - 1
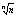 =1+xN =1+xN
n=(1+xN)n
n=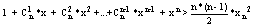
xN2<2/(n-1)
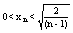 При n®¥ При n®¥ 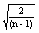 ®0 => xN®0 (Лемма о зажатой последовательности)=>Lim ®0 => xN®0 (Лемма о зажатой последовательности)=>Lim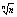 =Lim (1+xN)=1+0=1 =Lim (1+xN)=1+0=1
16.Последовательность (1+1/n)n и ее предел.
xN=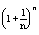 ; yN= ; yN=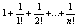 ; zN=yN + ; zN=yN +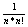
xN монотонно возрастает: докажем:
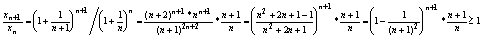
xN=(1+1/n)n=1+ n/1!*1/n + n*(n-1)/2!*1/n2 +...
< 1 + 1/1! + 1/2!+...+1/n! = yN => yN<zN
<3
Воспользуемся неравенством Бернулли (1+x)n³1+nx, x>-1)
(доказывается по индукции):
x=1/n => (1+1/n)n³1+n/n=2
Получили: 2 £ xN<3 => xN - ограничена,
учитывая что xN - монотонно возрастает => xN -
сходится и ее пределом является число е.
17. Последовательности 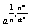 (во всех пределах n®¥) (во всех пределах n®¥)
1) Lim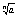 =1, a>0 =1, a>0
a) a³1:
xN=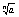 xN+1= xN+1=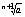 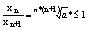 => $ Lim xN=x => $ Lim xN=x
xN+1=xN *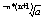
xN=xN+1 *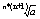
xN=xN+1*xN*(n+1)
Lim xN=Lim (xN+1*xN*(n+1)) => x = x*x => x = 1
б) 0<a<1 b=1/a xN=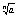
Lim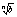 =1 b=1/a => =1 b=1/a =>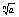 = 1/ = 1/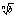 => Lim => Lim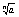 = 1/1 = 1 = 1/1 = 1
Страницы: 1, 2, 3, 4, 5, 6
| 


