|
(рис.8.4); метод Симпсона (парабол) учитывает еще и третий член разложения: 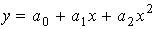
(рис.8.5).
Если 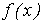 — «гладкая — «гладкая
функция», то можно вычислить 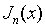
с 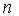 разбиениями разбиениями
отрезка 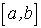 , а затем , а затем
удвоить число отрезков 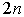
и снова вычислить эту площадь 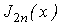
. Если 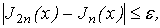 то то
вычисления завершаются. В противном случае число разбиений вновь увеличивается
вдвое до тех пор, пока не будет достигнута требуемая точность.
Очевидно, что величина погрешности зависит от характера функции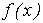
, ее поведения на концах отрезка интегрирования, следовательно, никакой
численный метод не может быть рекомендован как универсальный. Применение
конкретного метода зависит от вида подынтегральной функции 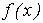
.
Б. Не вдаваясь в математические тонкости выведения формул погрешностей
вычисления интеграла различными методами, приведем лишь сами формулы.
(Любознательных читателей, интересующихся выводами, отсылаем к учебникам по
математическому анализу, например [3,4]). Итак, формулы для оценки погрешности
численного интегрирования методом:
1) прямоугольников (обычным и модифицированным)
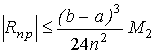 (8.7.а) (8.7.а)
2) трапеций
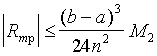 (8.7.б) (8.7.б)
3) Симпсона
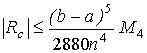 (8.7.в) (8.7.в)
где 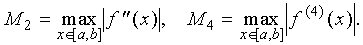
Очевидно, формула Симпсона обладает повышенной точностью:
1) она оказывается точной для 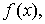
являющихся полиномами до третьей степени включительно, т.к. для этих случаев
производная четвертого порядка равна нулю;
2) для достижения той же точности, что и в формуле трапеций, в формуле Симпсона
можно брать меньшее число 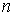
отрезков разбиения.
В. Выше уже рассматривалась процедура оценки одномерных определенных
интегралов, т.е. для выбранной классической формулы интегрирования вычисляются 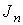
и 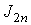 для приемлемого для приемлемого
значения 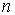 . Сходится . Сходится
ли последовательность 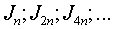
к истинному значению интеграла 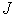
и существует ли какой-нибудь способ экстраполяции к пределу?
Рассмотрим этот вопрос на примере метода прямоугольников. Т.к. погрешность
приближения в методе убывает как 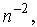
то 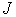
—экстраполированное значение связано с 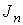
— значением интеграла при 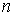
разбиениях соотношением:
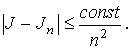
Отсюда сходимость данной последовательности очевидна.
Следовательно, формула прямоугольников дает последовательность
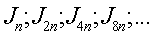
сходящуюся к некоторому числу 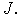
Т.к. ошибка метода трапеций имеет тот же порядок 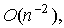
а метода Симпсона меньший порядок 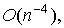
то очевидно, что последовательности 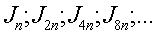
в методах трапеций и Симпсона также сходятся к некоторым пределам.
8.2.5 Численное интегрирование многомерных интегралов
классическими методами
Все геометрические и механические величины, связанные с плоским непрерывным
распределением массы вдоль некоторой фигуры, выражаются двойным интегралом.
Например, элементарные статические моменты и моменты инерции относительно осей
координат, а также координаты центра тяжести плоской фигуры рассчитываются по
формулам, включающим в себя двойные интегралы. Многие физические задачи
содержат усреднение по нескольким переменным, требующее вычисления многомерных
интегралов порядка 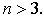
Таким образом, встает задача о вычислении многомерных интегралов.
Рассмотрим численное интегрирование классическими методами на самом простом
примере двойного интеграла
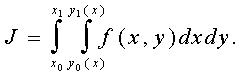 (8.8) (8.8)
Определим некоторую функцию 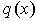 как внутренний интеграл по переменной как внутренний интеграл по переменной 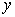
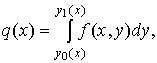 (8.9) (8.9)
тогда 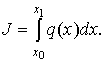
(8.10)
Для расчета интеграла (8.9) отрезок интегрирования 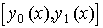
необходимо разбить на 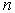
частей; разобъем для простоты отрезок 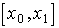
также на 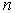 частей и частей и
вычислим интегральную сумму для (8.9) по 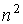
точкам одним из описанных классических методов. Очевидно, для расчета интеграла
третьего порядка потребуется считать сумму по 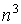
точкам, для 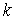 -мерного -мерного
интеграла — по 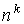
точкам. Понятно, что для больших значений 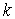
обычные численные методы становятся неприемлемыми. Для таких расчетов
применяется метод Монте-Карло.
8.3 Метод Монте - Карло
Основывается на теореме о среднем: если на отрезке 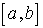
задана некоторая непрерывная интегрируемая функция 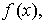
то найдется такая точка, принадлежащая этому отрезку, что справедлива формула
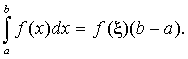 (8.11) (8.11)
Т.е. площадь криволинейной трапеции 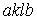
можно заменить площадью прямоугольника 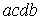
, одной из сторон которого является отрезок 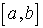
, а численное значение другой стороны — 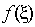
(рис.8.6).
Выберем на отрезке 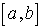 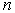 случайных точек случайных точек 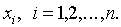 Можно Можно
показать, что при достаточно большом 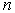 выполняется условие выполняется условие
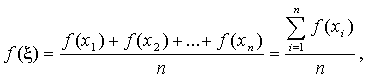
т.е. 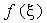 — среднее между ординатами случайно выбранных точек — среднее между ординатами случайно выбранных точек 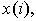
Страницы: 1, 2, 3, 4, 5, 6, 7
| 


