|
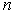 — количество испытаний (случайных выборок). — количество испытаний (случайных выборок).
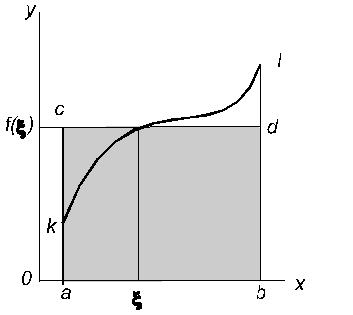
Рис.8.6
Для двойного интеграла метод Монте-Карло дает следующую формулу интегрирования:
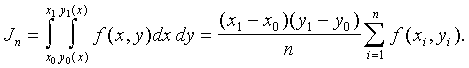
(8.12)
где 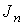 — оценка — оценка 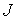 для для 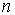 случайных выборок; случайных выборок;
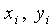 — независимые случайные числа на отрезках — независимые случайные числа на отрезках
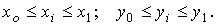
Метод Монте-Карло, как и классические методы, дает приближенные результаты.
Погрешность метода Монте-Карло
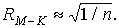 (8.13) (8.13)
В отличие от классических методов эта погрешность не зависит от вида
подынтегральной функции и от кратности интеграла. Заметим, что ошибку можно
сделать сколь угодно малой, либо увеличивая число испытаний 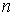
, либо применяя дополнительно методы существенной выборки или случайного
блуждания (интересующихся этим вопросом отсылаем к теории вероятностей).
8.4 Примеры
Пример 1. Вычислить интеграл 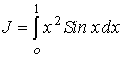
по формуле трапеций, разделив отрезок 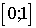
на 10 равных частей, и оценить погрешность вычислений.
Оценим ошибку метода. Для этого найдем вторую производную подынтегральной
функции:
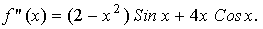
На отрезке 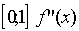 всюду всюду
положительна, причем ее значение ограничено сверху: 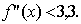
Таким образом, используя формулу (8.7.б) 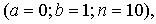
имеем:
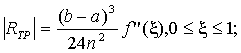
полагая 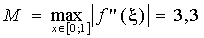 , получим , получим 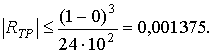
Итак, приняв на заданном участке интегрирования 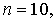
мы сможем получить интеграл от заданной функции с погрешностью, не превышающей
0,001375, если будем вести вычисления таким образом, чтобы погрешность
округления не исказила окончательный результат в пределах точности метода.
В соответствии с формулой трапеций (8.3) и учетом рассчитанной ошибки получим 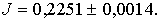
Пример 2. Вычислить интеграл из примера 1 по формуле Симпсона при том же
числе отрезков разбиения 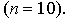
Для оценки остаточного члена найдем производную четвертого порядка от
подынтегральной функции 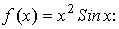
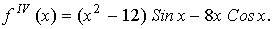
Значение 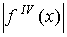 на отрезке на отрезке 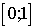
ограничено числом 14. Используя формулу (8.7.в), получаем оценку:
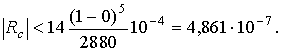
Приведем полученный результат в соответствии с оценкой
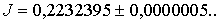
Сравнивая этот результат со значением интеграла, полученным в примере 1,
заметим, что при одинаковом числе отрезков разбиения формула Симпсона дает
ответ с большим числом верных знаков.
Посмотрим, как можно было бы воспользоваться в данном случае формулой (8.7.в).
Пусть требуется найти значение заданного интеграла с точностью 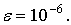
Тогда по формуле (3.7.в) получим:
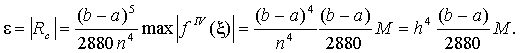
Отсюда
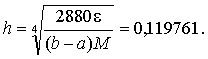
Следовательно, для достижения точности 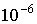
достаточно было разбить отрезок 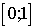
на 9 частей.
Пример 3. Вычислить интеграл из примера 1 по формуле Симпсона
методом повторного счета.
В 8.2.4 уже отмечалось, что существует прием, позволяющий не делать
рассмотренную выше оценку точности вычисления. А именно: искомый интеграл
вычисляется дважды. Для оценки погрешности, например, метода трапеций при этом
может использоваться простая формула. Пусть 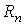
и 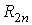 — погрешности — погрешности
интегрирования по формуле трапеций соответственно при 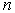
и 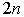 отрезках отрезках
разбиения. Учитывая приведенную оценку, можно составить равенство
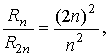 отсюда отсюда 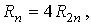 следовательно, следовательно, 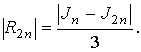
Полученная формула удобна для практической оценки погрешности метода
трапеций, но требует двойного счета (аналогично получаются формулы и для всех
остальных рассмотренных методов). Из оценочных формул (8.7) следует, что
ошибка интегрирования уменьшается с уменьшением шага интегрирования. На
основании этого хотелось бы сделать вывод, что при последовательном
увеличении числа отрезков разбиения мы будем получать значения интеграла все
более и более близкие к истинному. Но в процессе практических вычислений при
последовательном удвоении числа отрезков разбиения начинает сильно
увеличиваться удельный вес ошибки округления, значение которой с некоторого
момента ставит предел достижимой точности результата интегрирования. Итак,
если требуемая точность не достигается, в программе должен предусматриваться
повторный счет с шагом, уменьшенным вдвое. Схема соответствующего алгоритма
приведена на рисунке 8.7.
В блок-схеме буквами 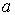 и и 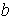 обозначены концы отрезков интегрирования; обозначены концы отрезков интегрирования;
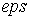 — точность расчета; — точность расчета;
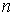 — первоначальное число отрезков разбиения. — первоначальное число отрезков разбиения.
ввод a, b, eps, n
J(n) = 0
h = (b - a)/n, S = (f(a) - f(b))/2
x = a + h
S = S + 2f(x) + f(x + h)
 x = x + h x = x + h
x < b да
 нет нет
J(2n) = 2hS/3, n = 2n
M = J(n) - J(2n), J(n) = J(2n)
Страницы: 1, 2, 3, 4, 5, 6, 7
| 


