|
поля направлений.
В качестве иллюстрации возьмем уравнение 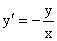 . .
Для построения поля направлений удобно использовать метод изоклин. Изоклина это
линия в каждой точке которой вектор 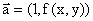
поля направлений одинаков. Таким образом, изоклины даются уравнением f(x,y)=l,
и каждой точке изоклины соответствует вектор 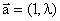
.
Для рассматриваемого дифференциального уравнения изоклины задаются уравнением 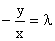
или y=-lx.
Как видно, изоклинами являются прямые, проходящие через точку начала координат.
На рис. 2 изображены изоклины отвечающие значениям 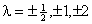
, черточками изображены направления векторов 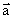
в таких изоклин. Из рис. 2 видно, что интегральные кривые уравнения напоминают
гиперболы. Действительно, как будет показано ниже, общее решение
рассматриваемого дифференциального уравнения имеет вид yx=c, т.е. задает
семейство гипербол. Параметрам c>0 отвечают гиперболы I и III координатных
узлов, значениям c<0 отвечают гиперболы II и IV координатных узлов.
3. Существование решения дифференциального уравнения первого порядка.
Задано дифференциальное уравнение вида
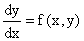 или, иначе, или, иначе, 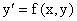 . .
Пусть y=y(x) – решение данного уравнения, удовлетворяющее начальному условию y(x
0)=y0. Тогда из 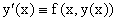
следует, что f(x,y(x)) – производная функции y(x) и, следовательно, y(x) –
первообразная для f(x,y(x)). Если F(x) – некоторая другая первообразная для
f(x,y(x)), то , как известно, y(x)=F(x)+c0. Из y(x0)=y
0, y(x0)=F(x0)+c0 получаем c0
=y0-F(x0), т.е. y(x)=F(x)-F(x0)+y0.
Семейство всех первообразных для f(x,y(x)) представляется неопределенным
интегралом 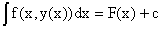 . Тогда . Тогда
разность F(x)-F(x0) равна значению определенного интеграла 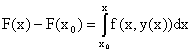
,
И, следовательно, получаем
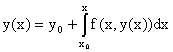 , ,
т.е. y(x) является решением интегрального уравнения
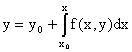 . .
Задача поиска решения дифференциального уравнения 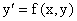
, удовлетворяющего начальному условию y(x0)=y0, получила в
литературе название задачи Коши.
Первое доказательство существования и единственности решения дифференциального
уравнения 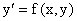 было было
получено в 1820-1830 г.г. и связано с именем Коши (1789-1857).
Теорема. Пусть задано уравнение 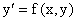 и начальные значения x0,y0. и начальные значения x0,y0.
Тогда если
А) функция f(x,y) непрерывна по обеим переменным x и y в замкнутой области 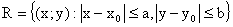 ; ;
Б) функция f(x,y) удовлетворяет в областиR по переменной y условию Липшица, т.е. 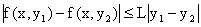
, где L – постоянная;
То существует единственное решение y=y(x) указанного уравнения, удовлетворяющее
начальному условию y(x0)=y0 и являющееся непрерывно
дифференцируемым в интервале 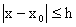
, где 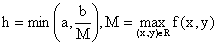 . .
Доказательство теоремы приводить не будем, укажем лишь, что может быть
осуществлено методом последовательных приближений Пикара (1856-1941),
использующего ранее приведенное интегральное уравнение.
Последовательность функций, дающих приближенное решение уравнения, строится
по правилу:
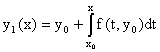 , ,
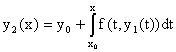 , ,
............
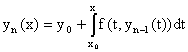 . .
Далее можно показать, что функция 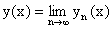
дает единственное решение дифференциального уравнения 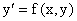
в промежутке 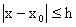 . .
Выше был рассмотрен случай дифференциального уравнения первого порядка
разрешенного относительно производной y/.
Более общим видом является случай уравнения вида 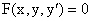
, не разрешимого относительно производной y/.
Допустим, что данное уравнение может быть разрешено относительно y/,
и в общем случае это дает несколько вещественных уравнений 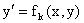
(k=1,2,.,m).
Если при этом каждая из функций 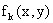
(k=1,2,.,m) удовлетворяет теореме существования и единственности решения, то
через точку (x0,y0) будет проходить m интегральных кривых
уравнения 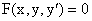 . Пусть . Пусть
при этом каждая точка кривой имеет свой наклон касательной, отличный от других
кривых. В этом случае также говорят, что задача Коши имеет единственное
решение. Общим решением уравнения называют совокупность всех общих решений
каждого из уравнений 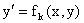
(k=1,2,.,m), т.е. решения y=Yk(x,c) (k=1,2,.,m).
Пример. Рассматривается дифференциальное уравнение вида  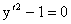
. Разрешая его относительно y/ получаем два уравнения y/=1
и y/=-1, т.е. через каждую точку плоскости xOy проходят две
интегральные кривые, касательные к которым имеют два разных угла наклона к оси
Ox в 450 и 1350. Общим решением уравнения будет семейство
интегральных кривых y=x+c и y=-x+c.
Особым решением дифференциального уравнения
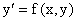 или или 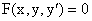
называется решением y=y(x), которое во всех своих точках не обладает
свойством единственности. Через каждую точку такого решения проходит не менее
двух интегральных кривых, имеющих одинаковое направление касательной.
Отметим, что из сказанного выше следует, что дифференциальное уравнение может
иметь решения не являющиеся ни частными, ни особыми, а именно, если эти
решения получаются склеиванием кусков из частных и особых решений.
4. Особые решения дифференциального уравнения.
Пусть рассматривается дифференциальное уравнение первого порядка общего вида
F(x,y,y/)=0.
Тогда существование его особого решения прежде всего может быть связано с
условием 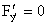 , не , не
обеспечивающим представление y/ как неявной функции переменных x и
y, задаваемой уравнением F(x,y,y/)=0.
Таким образом, формируя систему уравнений
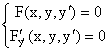 , ,
и исключая из нее переменную y/, получаем функцию y=y(x), которая
может дать особое решение дифференциального уравнения F(x,y,y/)=0.
Определение. Кривая, получаемая исключением параметра p из системы уравнений
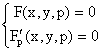 , ,
называется дискретной кривой уравнения F(x,y,y/)=0.
Для того, чтобы дискретная кривая давала особое решение дифференциального
уравнения, остается проверить, что она удовлетворяет уравнению F(x,y,y/
)=0, и что через каждую ее точку проходит хотя бы одна интегральная кривая
общего решения этого уравнения, т.е. проверить, что в точках дискретной кривой
нарушается свойство единственности решения дифференциального уравнения.
Пример 1. Дано уравнение 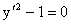 . .
Как было указано выше его особое решение дается уравнениями y=x+c и y=-x+c.
Опреляя для него дискретную кривую имеем систему уравнений
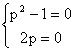 . .
Очевидно, данная система решения не имеет, поэтому рассматриваемое
дифференциальное уравнение особых решений не имеет.
Пример 2. Рассмотрим решение уравнения 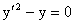
Его общее решение имеет вид 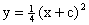 . Выписывая систему уравнений . Выписывая систему уравнений
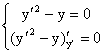 или или 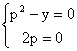 , (где p=y/) , (где p=y/)
и исключая из нее переменную p, получаем уравнение дискретной кривой y=0 (ось
Ox). Очевидно, она является решением дифференциального уравнения, так как из
y=0=const следует y/=0. Кроме того через любую точку M(x0
;0) этой кривой проходит частное решение дифференциального уравнения, получаемое
из общего при c=-x0. Не трудно убедиться, что касательные в точке
M(x0;0) дискретной кривой и частного решения совпадают. Таким
образом, дискретная кривая y=0 является особым решением исходного
дифференциального уравнения.
Ниже на рис. 3 изображено семейство интегральных кривых этого уравнения,
являющееся семейством парабол.
Из рисунка видно, что дискретная кривая y=0, являющаяся осью Ox, касается в
каждой точке некоторой кривой семейства.
Выше была рассмотрена ситуация, когда уравнение F(x,y,y/)=0 не
Страницы: 1, 2, 3, 4, 5, 6, 7
| 


