|
Действительно, подставляя в это уравнение u/x(x,c), получаем тождество
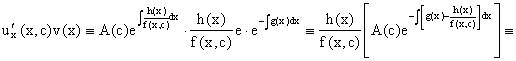
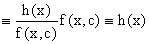 . .
Таким образом, показано, что общее решение линейного дифференциального уравнения 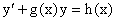
Представляется в виде y=u(x,c)v(x), где v(x) – частное решение однородного
уравнения 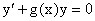 , ,
решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x).
Нетрудно видеть, что в обоих случаях приходится решать уравнение с
разделяющимися переменными.
Заметим, что хотя при решении однородного уравнения 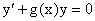
бралось частное решение V(x) однородного уравнения v/+g(x)v=0,
Являющегося уравнением с разделяющимися переменными.
На втором этапе определяется решение u(x,c) дифференциального уравнения u/
v(x)=h(x),
Также являющегося уравнением с разделяющимися переменными. После их решений
общее решение исходного линейного уравнения представляется в виде
Y=u(x,c)v(x).
Пример 1. Решить уравнение
Y/+2y=sinx.
Сначала решаем однородное уравнение v/+2v=0.
Из него получаем
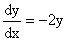 или или 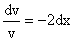 . .
Интегрируя его левую и правую части, получаем его общий интеграл (решение) вида
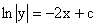 . .
Полагая в нем c=0 и потенциируя его, получаем следующее его нетривиальное
частное решение 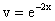 . .
Далее решаем уравнение вида
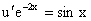 или или 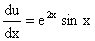 . .
Разнося переменные в разные части уравнения и интегрируя их, получаем общее
решение этого уравнения
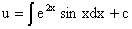 . .
Вычислим интеграл:
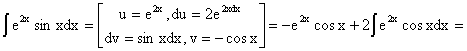
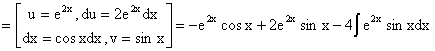
.
Рассматривая данное уравнение, как уравнение относительно интеграла, находим
его вид
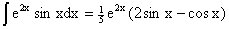 . .
Следовательно, 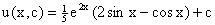 . .
Тогда общее решение исходного уравнения будет
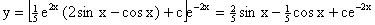 . .
Предположим теперь, что требуется выделить частное решение, проходящее через
точку M(0,0), т.е. решение, удовлетворяющее начальному условию y(0)=0. Для
этого подставим значения x=0, y=0 в общее решение и найдем соответствующее
значение постоянной c:
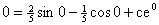 , отсюда , отсюда 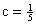 . .
Искомым частным решением является
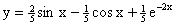 . .
Пример 2. Решить уравнение
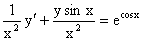 , ,
являющееся линейным дифференциальным уравнением.
На первом этапе найдем решение соответствующего линейного однородного уравнения
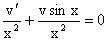 , или , или 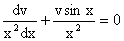 . .
Разделяя переменные по разные стороны уравнения, имеем
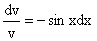 . .
Интегрируя обе части данного уравнения, получаем следующее его частное решение
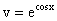 . .
На втором этапе решаем уравнение вида
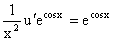 . .
Делая замену 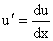 , ,
сокращая обе части уравнения на 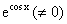
и разделяя переменные, имеем du=x2dx.
Интегрируя правую и левую части уравнения, получаем его общее решение
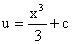 . .
Общее решение исходного дифференциального уравнения имеет вид
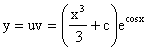 . .
8. Дифференциальное уравнение первого порядка в полных дифференциалах.
Определение. Пусть дифференциальное уравнение первого порядка представлено в
виде
M(x,y)dx+N(x,y)dx=0,
Где M(x,y) и N(x,y) – функции двух переменных x и y. Тогда, если левая часть
уравнения есть полный дифференциал некоторой функции U(x,y), т.е.
dU(x,y)=M(x,y)dx+N(x,y)dy,
то такое уравнение называется уравнением в полных дифференциалах.
Уравнение в полных дифференциалах кратко можно представить в виде
dU(x,y)=0,
а поэтому общий интеграл (решение) такого уравнения имеет вид U(x,y)=0.
Дифференциальное уравнение такого типа возникает, когда поведение системы
подчинено условию сохранения некоторой величины U(энергии, массы, стоимости и
т.д.).
Отметим следующий признак, позволяющий определить является ли рассматриваемое
уравнение уравнением в полных дифференциалах.
Путьс
dU(x,y)=M(x,y)dx+N(x,y)dy, тогда функции M(x,y) и N(x,y) должны быть для
U(x,y) частными производными первого порядка, соответственно, по переменным x
и y, т.е.
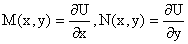 . .
Предполагая функции M(x,y) и N(x,y) непрерывными и имеющими непрерывные
частные производные, соответственно, по y и x, т.е. выполнение соотношений
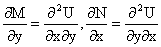 , ,
из тождества
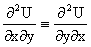
получаем, что для M(x,y) и N(x,y) должно выполняться условие
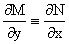 . .
Полученное условие является не только необходимым, но и достаточным для того,
чтобы уравнение M(x,y)dx+N(x,y)dy=0
Было уравнением в полных дифференциалах.
Нахождение общего решения уравнения в полных дифференциалах проводится в два
этапа.
На первом этапе функция U(x,y) рассматривается как функция только аргумента x,
переменная y получает как бы фиксированное значение 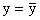
. Тогда соотношению
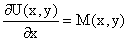
ставится в соответствие дифференциальное уравнение
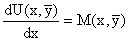 . .
Пусть его общее решение представляется в виде
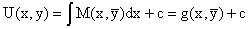 . .
Но так как решение уравнения зависит от y, то в общем решении постоянная c
является функцией y, т.е. c=h(y). Следовательно, общее решение предыдущего
дифференциального уравнения, снимая с y условие закрепления его значения,
имеет вид
U(x,y)=g(x,y)+h(y).
На втором этапе находится вид функции h(y). Для этого обратимся к соотношению
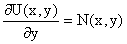 , ,
в котором уже закрепляется как бы значение переменной x.
Используя данное соотношение и вид функции U(x,y), получаем дифференциальное
уравнение, связывающее переменные h и y:
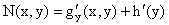 или или 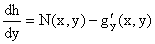 . .
Интегрируя это уравнение, находим его общее решение
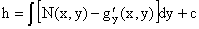 . .
Из 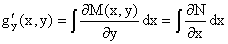 , получаем окончательный вид функции U(x,y), а именно , получаем окончательный вид функции U(x,y), а именно
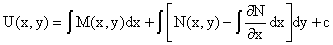 или или
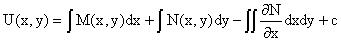 . .
В последнем двойном интеграле вместо 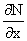
можно взять функцию 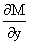
(т.к. 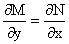 ). Тогда ). Тогда
функция U(x,y) получает вид
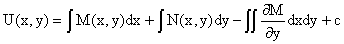 . .
Так как общее решение исходного дифференциального уравнения записывается в
виде U(x,y)=c=const, то, заменяя две постоянных на одну, получаем следующий
вид общего решения уравнения
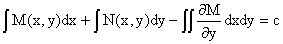 или или
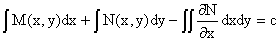 . .
Пример 1. Дано дифференциальное уравнение
(6x2y2+6xy-1)dx+(4x3y+3x2y+2y)dy=0.
В нем M(x,y)=6x2y2+6xy-1, N(x,y)=4x3y+3x2y+2y. Из 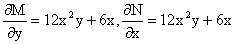 и тождества и тождества 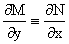 , ,
Следует, что данное уравнение является уравнением в полных дифференциалах.
Проведем его решение в два этапа.
Страницы: 1, 2, 3, 4, 5, 6, 7
| 


