|
2.6. Проверка гипотезы вида закона распределения вероятностей
При проверке эксперимента закон распределения вероятностей случайных величин
неизвестен и можно лишь предположительно судить о его виде . Выборочные
оценки параметров распределения несут в себе случайные ошибки, искажающие
истинный характер распределения. Поэтому после получения эмпирического
распределения производится подбор теоретического закона распределения,
пригодного для описания вероятностных свойств изучаемой случайной величины.
Критерии подбора ( проверки гипотезы соответствия ) называют в статистике
критериями согласия. Все они основаны на выборе допустимой меры расхождения
между теоретическим распределением и выборочными данными.
Общую процедуру проверки гипотезы закона распределения можно представить в
следующей последовательности:
1. По опытным данным строится эмпирическая кривая распределения вероятностей;
2. Определяются параметры эмпирического распределения ( в соответствии с его
видом );
3. Выдвигается одна или несколько гипотез о функции плотности исследуемой
случайной величины, исходя из внешнего вида эмпирической кривой, значений ее
параметров, технических факторов, влияющих на ее вид;
4. Эмпирическая кривая выравнивается по одной или нескольким теоретическим
кривым;
5. Проводится сравнение по одному или нескольким критериям согласия;
6. Выбирается теоретическая функция, дающая наилучшее согласование.
Поясним п. 4; 5. Определив по эмпирическим данным параметры распределения,
подставляют их в теоретическую кривую закона распределения и рассчитывают
вероятность середин интервалов эмпирического распределения. Умножив значение
полученной вероятности на общее число опытов, получают теоретическое значение
частот случайной величины, которые и определяют ²выровненную²
кривую. Теперь можно найти вероятность того, что эмпирическая кривая
соответствует выбранной теоретической, выбрав вероятность согласия ( уровень
значимости ). Если результат расхождения не выйдет за принятый уровень
значимости, то считают, что эмпирическое распределение согласуется с
теоретическим. Если сравнение осуществляется с несколькими теоретическими
законами, то окончательно принимать тот, который дает лучшее соответствие.
Чаще всего в качестве критериев согласия принимают критерий Пирсона ( c2
) и критерий Колмогорова - Смирнова ( К - С - критерий ).
Критерий c2 является наиболее состоятельным при большом числе
наблюдений. Он почти всегда опровергает неверную гипотезу, обеспечивает
минимальную ошибку в принятии неверной гипотезы по сравнению
с другими критериями.
c2 = 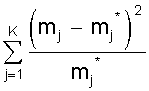 , ,
где mj - наблюдаемая частота случайного события;
m*j - ожидаемая по принятому теоретическому закону распределения;
К - число интервалов случайной величины.
Затем определяется число степеней свободы l:
l = К - r - 1;
где К - число интервалов случайной величины;
r - число параметров теоретической функции распределения.
К - С - критерий лучше всего использовать в случае, если теоретические
значения параметров распределения известны. При неизвестных параметрах его
можно использовать, но он дает несколько завышенные результаты. При
использовании этого критерия определяется величина
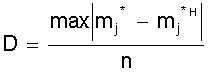 , ,
где
mнj, m*нj - соответственно, накопленные наблюдаемые и ожидаемые
(теоретические) частоты;
n - число проведенных опытов.
То есть, в данном случае оценивается только максимальное отклонение
накопленной частоты случайного события, возникающее в одном из диапазонов
изменения случайной величины. Полученное значение коэффициента сравнивается с
табличным для числа степеней свободы опыта и принятого уровня значимости
результата. Если табличное значение коэффициента больше, то гипотеза о
принятом законе распределения не отвергается.
Контрольные вопросы
1. Сущность непрерывной и дискретной случайной величины;
2. Сущность интегрального закона распределения случайной величины;
3. Сущность дифференциального закона распределения случайной величины;
4. Связь интегрального и дифференциального законов распределения;
5. Основные характеристики случайной величины, заданной своим распределением;
6. Назовите примеры законов распределения непрерывной и дискретной случайной
величины;
7. Понятие статистической гипотезы и статистического критерия;
8. Назовите примеры статистических гипотез;
9. Сущность ошибок первого и второго рода;
10. Сущность проверки гипотезы вида закона распределения;
11. Принципиальное различие в критериях Пирсона и Колмогорова - Смирнова.
3. НАХОЖДЕНИЕ ИНТЕРПОЛИРУЮЩИХ КРИВЫХ
В первой части пособия рассматривались измерения той или иной физической
величины, находящейся при проведении серии измерений в неизменном состоянии.
Очень часто исследуемая величина меняется в соответствии с изменением условий
опыта или времени. Цель эксперимента в этом случае состоит в нахождении
функциональной зависимости, которая наилучшим образом описывает изменение
интересующего нас параметра.
Следует понимать, что однозначно восстановить ( большей частью неизвестную )
функциональную зависимость между переменными невозможно даже в том случае,
если бы переменные величины, полученные из опыта, не имели бы ошибки
измерения. Тем более не следует ожидать, что это удастся сделать, имея
экспериментальные данные, содержащие, по крайней мере, случайные ошибки
измерений.
Поэтому математическая обработка результатов наблюдений не может ставить
перед собой задачу разгадать истинный характер зависимости между переменными.
Она позволяет лишь представить результаты опыта в виде наиболее простой
формулы.
В зависимости от назначения этих формул существуют различные методы их
получения, отличающиеся сложностью расчетных процедур и точностью получаемых
решений.
3.1. Графический метод обработки результатов
Графический метод заключается в построении графика зависимости между
исследуемыми величинами с последующим определением уравнения зависимости
между ними.
Графики строят прежде всего в равномерных шкалах. Если характер связи между
исследуемыми величинами неизвестен, то сначала проверяют совпадение
экспериментальных точек с заданной кривой. Если предварительные сведения о
характере уравнения отсутствуют, то первым этапом обработки данных является
нахождение кривой, совпадающей с опытными точками. Эта задача решается
методом подбора. Можно использовать эталон - кальку с предварительно
вычерченным на ней семейством кривых с различными параметрами. Естественно,
что масштаб кальки и эмпирической кривой должен быть одинаков.
Построенный по опытным данным отрезок кривой может совпадать с большим
количеством различных кривых, проходящих достаточно близко к опытным точкам.
В этом случае выбирают кривую с наиболее простым и удобным в использовании
уравнением. Иногда эмпирическая кривая может иметь перегибы или состоять из
отдельных ярко выраженных участков. Однако при этом необходимо определить
координаты точек перехода от одной кривой к другой.
Уравнение зависимости между исследуемыми величинами при графическом методе
просто определяется тогда, когда эмпирические точки достаточно хорошо
совпадают с прямой линией, т.е. описываются уравнением y = ax + b, где a, b -
коэффициенты, подлежащие определению.
Определение коэффициентов при графическом методе основано на ²способе
натянутой нити². Нанеся результаты эксперимента на график (лучше, если он
выполнен на миллиметровке), подбираем графическую прямую, ближе всего
подходящую к нанесенным точкам. Выбрав положение прямой, определяем две
произвольные точки на этой прямой (не обязательно являющиеся точками
эксперимента), определяем их координаты (x1; y1), (х
2; y2). И для определения коэффициентов а и b получаем два
простых уравнения
ах1 + b = y1;
ах2 + b = y2.
На рис. 10 приведена иллюстрация этого метода. Точки - результаты, полученные
в эксперименте. Прямая проведена на глаз как можно ближе к экспериментальным
точкам. На прямой выбраны точки М (2; 4) и N (13; 10). Коэффициент а
характеризует угол наклона прямой.
Поэтому
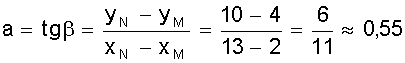
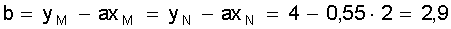
.
Таким образом y = 0,55х + 2,9.
Рис. 10. Графический метод интерполяции
В случае, если экспериментальная зависимость имеет нелинейный характер, то
графическим способом в системе координат с равномерными шкалами определить
коэффициенты кривой затруднительно. Но достаточно большой класс нелинейных
зависимостей путем замены переменных и графического изображения в
функциональных шкалах можно привести к линейным и далее использовать способ
натянутой нити.
3.2. Функциональные шкалы и их применение
Пусть функция y = ¦(х) непрерывна и монотонна на некотором промежутке [ a; b
]. Возьмем ось ОМ, на которой будет строиться шкала, выберем на ней точку
начала отсчета О и установим масштаб m. Функциональная шкала строится
следующим образом.
Разбив интервал [ а; b ] на равные части, вычисляем значение функции ¦(х) в
каждой из точек деления и отложим на оси ОМ для каждой точки отрезок m¦(х).
Получающаяся при этом точка снабжается отметкой х, т.е. откладывается в
выбранном масштабе значение функции, а надписывается значение аргумента.
Иногда начало шкалы помещают в первую точку отсчета, т.е. точку с надписью а
совмещают с 0. Тогда точка х будет находиться в конце отрезка m [ ¦(х) - ¦(а)
]. Полученная шкала позволяет судить о поведении функции на рассматриваемом
участке: большие промежутки между отметками укажут, что функция изменяется
быстрее, чем там, где эти промежутки малы.
Выбор масштаба m определяет длину шкалы. Чаще поступают наоборот: задаются
длиной шкалы l и определяют масштаб.
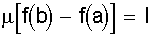 Þ m = Þ m = 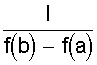 . .
Пример. Построим функциональную шкалу для функции y = x2 на участке [
1; 2 ]. Зададимся длиной шкалы l = 12 см. Тогда m = 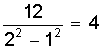
см. Разобьем отрезок [ 1; 2 ] на десять равных частей и вычислим значения
функции во всех точках деления. Совместим начало шкалы с точкой отсчета х = 1.
Результаты расчета сведены в табл. 2, а функциональная шкала приведена на рис.
11.
Таблица 2
Расчет функциональной шкалы y = x2
| х | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | х2 | 1,0 | 1,21 | 1,44 | 1,69 | 1,96 | 2,25 | 2,56 | 2,89 | 3,24 | 3,61 | 4,00 | х2-1 | 0 | 0,21 | 0,44 | 0,69 | 0,96 | 1,25 | 1,56 | 1,89 | 2,24 | 2,26 | 3,00 | 4(х2-1) | 0 | 0,84 | 1,76 | 2,76 | 3,84 | 5,00 | 6,24 | 7,56 | 8,94 | 10,44 | 12,0 |
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
| 


