1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0

Рис. 11. Функциональная шкала y = x2

С помощью функциональных шкал графики многих функций могут быть преобразованы

к прямолинейному виду.

Например, уравнение параболы y = x2. Если на оси OY нанести

равномерную шкалу, а на оси OX1 шкалу квадратов х1 = х

2, то получится сетка, где уравнение параболы имеет изображение прямой

линии ( y = x1 ),

проходящей через начало координат.

Особенно часто используются различные логарифмические функции, с помощью которых

можно ²выпрямлять² графики степенных и показательных функций.

Например, y = aebx; lg y = (b lg å) х + lg a. Полагая lg y = y

1, lg a = A, b lg e = B запишем исходное уравнение в виде y1 =

А + Вх, откуда видно, что оставив равномерной шкалу х и построив

логарифмическую шкалу y1, можно изобразить исходное уравнение прямой

линией. Полученная координатная сетка называется полулогарифмической.

Очевидно, что такого рода преобразования возможны и в более общем случае.

Всякая неявная функция, заданная соотношением вида

аj(х) + by(y) + с = 0,

где a, b, с - постоянные, будет изображаться прямой линией на функциональной

сетке, где на оси ОХ построена шкала j(х), а на оси OY - шкала функции y(y).

Естественно, что функции j(х) и y(y) должны удовлетворять условиям

непрерывности и монотонности. В табл. 3 приведены преобразования для

некоторых функций.

Таблица 3

Линеаризация некоторых функций

Исходная формула	Преобразованная формула	Замена переменных	Линеаризованная формула
y=axb	lg y=b×lgx+lga	lg y=y1 lg x=x1 lg a=a1	y1=bx1+a1
y=a×lgx+b	¾	lg x=x1	y=ax1+b
y=ebx+k	lg y=b×lge×x+k×lge	lg y=y1 b×lg e=a k×lg e=k1	y1=ax+k1
y=aebx	lg y=bx×lge+lga	lg y=y1 b×lg e=b1 lg a=a1	y1=b1x+a1
y=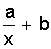	¾		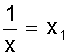y=ax1+b
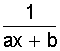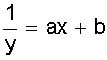
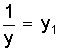
y=			y1=ax+b
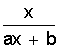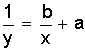
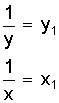
y=			y1=bx1+a

Из сказанного ясна роль функциональных сеток при обработке результатов

эксперимента. Если результаты эксперимента располагаются вблизи кривой, то по

имеющемуся ограниченному участку кривой трудно судить, какого типа функцией

ее лучше всего приближать. Переведя полученные экспериментальные данные на

функциональные сетки можно оценить на какой из них эти данные ближе всего

подходят к прямой и, следовательно, какой функцией лучше всего описываются.

3.3. Аналитические методы обработки результатов

Графический метод обработки результатов обладает наглядностью, относительной

простотой, однако его результаты содержат определенную субъективность и

относительно низкую точность.

Аналитические методы лишены в какой - то степени указанных недостатков и

позволяют получить результат для более широкого класса функций с большей

точностью, чем графический метод.

Существуют различные аналитические методы получения параметров эмпирических

кривых в зависимости от критерия, принятого при их получении. Рассмотрим

некоторые из существующих способов.

3.3.1. Способ средней

Допустим, что имеется n сочетаний xi, yi, полученных при

эксперименте. Даже в том случае, если между х и y теоретически установлена

функциональная связь ( в данном случае предположим, что линейная ), то

наблюдаемые значения yi будут отличаться от ахi + b

вследствие наличия экспериментальных ошибок. Обозначим через Di

соответствующую ошибку

Di = yi - axi - b (i = 1, 2, ..., n)

Если выбирать параметры а и b так, чтобы для всех n наблюдений ошибки

уравновешивались, т.е.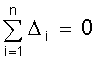

, то это привело бы нас к одному уравнению, тогда как для нахождения двух

коэффициентов (а, b) их требуется два. Поэтому предположим, что уравновешивание

происходит не только для всех произведенных наблюдений в целом, но и для каждой

группы, содержащей половину ( или почти половину ) всех наблюдений в

отдельности.

В этом случае можно прийти к системе уравнений

,

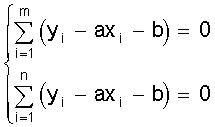где m - число наблюдений в первой группе.

Данную систему уравнений запишем теперь в виде

.

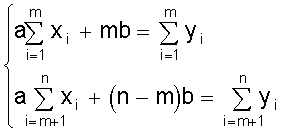Изложенное показывает, что метод средних ²уравновешивает²

положительные и отрицательные отклонения теоретической кривой от

экспериментальных значений.

Пример.Используя данные рис. 10 определим коэффициенты а, b методом средней.

Для этого семь измерений разделим на две группы m = 3 первых значений, n - m

= 4 последующих

; ;

; .

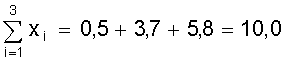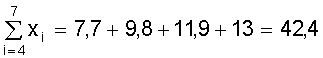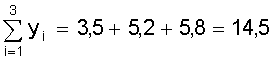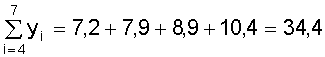Получаем систему

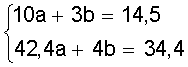
Решая систему находим

;

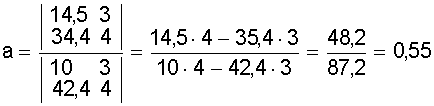
b =

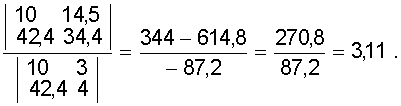
Таким образом способ средней дает прямую

y = 0,55х + 3,11.

В сравнении с графическим способом коэффициенты а совпадают и имеется

различие в коэффициенте b.

3.3.2. Метод наименьших квадратов

В методе средних при определении коэффициентов уравнения использовалось условие

равенства нулю алгебраической суммы отклонений результатов эксперимента от

теоретической кривой ( в частном случае прямой ). Очевидно, что при этом D

i могут быть значительной величины. Имеет значение только

²уравновешивание² положительных и отрицательных отклонений.

Поставим теперь задачу нахождения по результатам наблюдений наиболее

вероятные значения неизвестных коэффициентов.

Предположим, что искомая зависимость y = ¦(х) существует. Тогда параметры этой

линии необходимо выбрать таким образом, чтобы точки yi располагались

по обе стороны кривой y = ¦(х) как можно ближе к последней. Предположим, что

разброс точек yi относительно y = ¦(х) подчиняется закону

нормального распределения. Тогда мерой разброса является дисперсия s2

или ее приближенное выражение - средний квадрат отклонений.

.

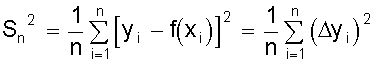И требование минимального разброса будет удовлетворено, если минимизировать

выражение ( Dyi )2. Как известно, необходимым условием

того, что функция приобретает минимальное значение, является то, что ее первая

производная ( или частные производные для функции многих переменных ) равна

нулю. Применение метода наименьших квадратов имеет смысл, если число

экспериментальных точек n больше числа определяемых коэффициентов.

Рассмотрим реализацию метода наименьших квадратов применительно к уравнению

вида y = ax + b.

Для нахождения коэффициентов а, b искомой прямой необходимо минимизировать сумму

квадратов расстояний Dyi по ординате от точки (хi; y

i) до прямой ( см. рис. 12 ). Расстояния Dyi определятся

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10