| Диплом: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле |
Диплом: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле
на тему: "Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле". |
Оглавление.
Введение.
§1. О задачах Дирихле.
а) Задача Дирихле для круга – Задача Пуассона (классическая формулировка).
б) Обобщенная задача Дирихле
в) Видоизмененная задача Дирихле.
г) Классическая задача Дирихле для многосвязных областей.
д) Общая формулировка задачи Дирихле.
е) Задача Неймана.
§2. О задачах Шварца-Пуассона.
а) Интеграл Шварца для круга.
б) Интегральная формула Пуассона.
в) Интеграл Пуассона для внешности круга.
г) Задача Дирихле-Пуассона для полуплоскости.
д) Задача Дирихле для кругового кольца.
§3. Интегральная формула Анри Вилля – проблема Дирихле для кругового кольца
(1912).
а) Преобразование интегральной формулы А.Вилля.
б) Функции Вейерштрасса (I(u), 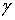 (u), (u), 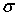 (u)).
§4. О некоторых изменениях теории конформного отображения к краевым задачам.
а) Об структурном классе интегральных представлений.
б) О решении задачи Дирихле методом Чизотти для многосвязных областей.
в) Интегральная формула Чизотти для заданных областей – решение задачи
Дирихле для соответствующих областей.
§5. Об интегральных представлениях Пуассона-Дирихле для заданных областей.
§6. Интегральная формула Чизотти-Пуассона-Дирихле для конечных трехсвязных
областей.
Литература.
Введение.
В данной дипломной работе исследованы некоторые интегральные формулы
(классические представления) аналитических и гармонических функций в заданных
многосвязных областях.
Даны новые методы решения классических краевых задач методом интегральных
представлений аналитических функций, используя метод конформного отображения
канонической области (u)).
§4. О некоторых изменениях теории конформного отображения к краевым задачам.
а) Об структурном классе интегральных представлений.
б) О решении задачи Дирихле методом Чизотти для многосвязных областей.
в) Интегральная формула Чизотти для заданных областей – решение задачи
Дирихле для соответствующих областей.
§5. Об интегральных представлениях Пуассона-Дирихле для заданных областей.
§6. Интегральная формула Чизотти-Пуассона-Дирихле для конечных трехсвязных
областей.
Литература.
Введение.
В данной дипломной работе исследованы некоторые интегральные формулы
(классические представления) аналитических и гармонических функций в заданных
многосвязных областях.
Даны новые методы решения классических краевых задач методом интегральных
представлений аналитических функций, используя метод конформного отображения
канонической области 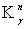 (z) на соответствующие области G
(z) на соответствующие области G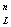 (w).
Используя фундаментальные интегральные формулы для круга и кругового кольца,
автор обобщает задачи Пуассона, Дирихле, Дини, Шварца, Кристофеля-Шварца и
Чизотти для многосвязных областей.
В частности, найдены интегральные формулы для эксцентрического кругового
кольца, двух-трехсвязных областей. И нашли применение их к решению
классических краевых задач типа Дирихле-Неймана.
Целью нашего исследования в предлагаемой работе являются:
1. Разобраться в вышеуказанных (непростых) известных классических задачах
типа Шварца, Дирихле, Пуассона и Чизотти [1] – [7].
2. Творчески изучая и классифицируя их, найти обобщение и решение этих
задач для конкретных многосвязных областей (см. оглавление).
Данная работа состоит из введения и 6 параграфов.
В введении обосновывается постановка задачи, показывается актуальность
рассматриваемой темы дипломной работы, дается краткий анализ и перечень работ
по данному исследованию (1 – 24).
Параграфы (§1, §2) не только вспомогательные материалы, необходимые для
понимания основного содержания дипломной темы, но и являются справочной
классификацией о задачах Дирихле (классическая, обобщенная, общая,
видоизмененная) для любой связности заданной области G
(w).
Используя фундаментальные интегральные формулы для круга и кругового кольца,
автор обобщает задачи Пуассона, Дирихле, Дини, Шварца, Кристофеля-Шварца и
Чизотти для многосвязных областей.
В частности, найдены интегральные формулы для эксцентрического кругового
кольца, двух-трехсвязных областей. И нашли применение их к решению
классических краевых задач типа Дирихле-Неймана.
Целью нашего исследования в предлагаемой работе являются:
1. Разобраться в вышеуказанных (непростых) известных классических задачах
типа Шварца, Дирихле, Пуассона и Чизотти [1] – [7].
2. Творчески изучая и классифицируя их, найти обобщение и решение этих
задач для конкретных многосвязных областей (см. оглавление).
Данная работа состоит из введения и 6 параграфов.
В введении обосновывается постановка задачи, показывается актуальность
рассматриваемой темы дипломной работы, дается краткий анализ и перечень работ
по данному исследованию (1 – 24).
Параграфы (§1, §2) не только вспомогательные материалы, необходимые для
понимания основного содержания дипломной темы, но и являются справочной
классификацией о задачах Дирихле (классическая, обобщенная, общая,
видоизмененная) для любой связности заданной области G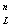 = G
= G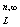 (w)
и задачах Шварца-Пуассона (для круга, кругового кольца, внешности кругов, для
полуплоскости).
В §3 интегральная формула Анри Вилля – проблема Дирихле для кругового кольца в
форме Ахиезера преобразована и получена новая компактная, контурная,
структурная формула А.Вилля для кругового кольца. Здесь же, ввиду важности трех
функций I(u), (w)
и задачах Шварца-Пуассона (для круга, кругового кольца, внешности кругов, для
полуплоскости).
В §3 интегральная формула Анри Вилля – проблема Дирихле для кругового кольца в
форме Ахиезера преобразована и получена новая компактная, контурная,
структурная формула А.Вилля для кругового кольца. Здесь же, ввиду важности трех
функций I(u), 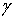 (u) и
(u) и 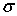 (u
) для практического приложения и простоты реализации на ЭВМ, мы рассмотрели все
варианты представления рядов данных функций (37) – (48) по справочникам [19] –
[22] специальных функций (а), б)).
Параграфы §4 - §6 – основное содержание самостоятельной работы автора:
рассмотрены применение теории комфорного отображения к краевым задачам –
решение задачи Дирихле методом Чизотти для заданных областей (§4).
В §5 – интегральные представления Пуассона-Дирихле для круга, кругового
кольца и, наконец, §6 – интегральная формула Чизотти-Шварца-Пуассона-Дирихле
для конечных трехсвязных областей.
Оглавление – ясное представление о единстве всех классических задач и о
содержании предлагаемой работы (см. оглавление!).
В данной работе все найденные решения выписываются почти в явном виде и
параметры, фигурирующие в постановке задачи, определяются явно и однозначно.
Основное содержание дипломной работы являются некоторыми обобщениями курсовых
работ и самостоятельной работы автора.
§1. О задачах Дирихле.
а) Задача Дирихле для круга – Задача Пуассона
(классическая формулировка).
1. Задача нахождения функции, гармонической в некоторой области была названа
Риманом задачей Дирихле. В классическом виде эта задача формулируется
следующим образом.
Пусть на границе (u
) для практического приложения и простоты реализации на ЭВМ, мы рассмотрели все
варианты представления рядов данных функций (37) – (48) по справочникам [19] –
[22] специальных функций (а), б)).
Параграфы §4 - §6 – основное содержание самостоятельной работы автора:
рассмотрены применение теории комфорного отображения к краевым задачам –
решение задачи Дирихле методом Чизотти для заданных областей (§4).
В §5 – интегральные представления Пуассона-Дирихле для круга, кругового
кольца и, наконец, §6 – интегральная формула Чизотти-Шварца-Пуассона-Дирихле
для конечных трехсвязных областей.
Оглавление – ясное представление о единстве всех классических задач и о
содержании предлагаемой работы (см. оглавление!).
В данной работе все найденные решения выписываются почти в явном виде и
параметры, фигурирующие в постановке задачи, определяются явно и однозначно.
Основное содержание дипломной работы являются некоторыми обобщениями курсовых
работ и самостоятельной работы автора.
§1. О задачах Дирихле.
а) Задача Дирихле для круга – Задача Пуассона
(классическая формулировка).
1. Задача нахождения функции, гармонической в некоторой области была названа
Риманом задачей Дирихле. В классическом виде эта задача формулируется
следующим образом.
Пусть на границе 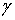 области D+ задана непрерывная функция f(
области D+ задана непрерывная функция f(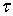 ). Найти непрерывную в
). Найти непрерывную в 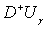 и гармоническую внутри области D+ функцию U(z
), принимающую на границе значения f(
и гармоническую внутри области D+ функцию U(z
), принимающую на границе значения f(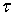 ). Таким образом, требуется, чтобы U(z) стремилась к f(
). Таким образом, требуется, чтобы U(z) стремилась к f(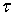 ), когда z
), когда z 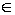 D+ стремится к
D+ стремится к 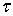 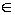 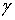 , u(z) → f(
, u(z) → f(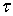 ), при z →
), при z → 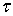 .
Задача Дирихле представляет интерес для физики. Так, потенциал
установившегося движения несжимаемой жидкости, температура, электромагнитные
и магнитные потенциалы – все являются гармоничными функциями.
Примером физической задачи, приводящей к задаче Дирихле, служит определение
температуры внутри пластинки при известных ее значениях на контуре.
Из других физических задач возникла формулировка задачи Неймана. Найти
гармоническую в области D+ функцию U(z) по
заданным значениям ее нормальной производной
.
Задача Дирихле представляет интерес для физики. Так, потенциал
установившегося движения несжимаемой жидкости, температура, электромагнитные
и магнитные потенциалы – все являются гармоничными функциями.
Примером физической задачи, приводящей к задаче Дирихле, служит определение
температуры внутри пластинки при известных ее значениях на контуре.
Из других физических задач возникла формулировка задачи Неймана. Найти
гармоническую в области D+ функцию U(z) по
заданным значениям ее нормальной производной 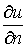 на
на 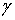 , а также
смешанной задачи Дирихле-Неймана.
Найти гармоническую в D+ функцию по известным ее значениям на
некоторых дугах границы , а также
смешанной задачи Дирихле-Неймана.
Найти гармоническую в D+ функцию по известным ее значениям на
некоторых дугах границы 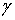 и значениям нормальной производной на остальной части
и значениям нормальной производной на остальной части 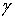 .
Смешанная задача встречается главным образом в гидродинамике. Различные
приложения этих задач можно найти, например, в книге Лаврентьев И.А. и Шабат
Б.В. [1].
Итак, по многочисленности и разнообразию приложений задача Дирихле занимает
исключительное место в математике. К ней непосредственно сводится основная
задача в гидродинамике – задача обтекания, задачи кручения и изгиба в теории
упругости. С нею же тесно связаны основные задачи статистической теории
упругости. Мы будем заниматься плоской задачей, которая представляет для нас
особый интерес как по обилию приложений, так и по большей разработанности и
эффективности методов решения.
2. Совокупность гармонических функций – это совокупность всех решений
уравнения Лапласа
.
Смешанная задача встречается главным образом в гидродинамике. Различные
приложения этих задач можно найти, например, в книге Лаврентьев И.А. и Шабат
Б.В. [1].
Итак, по многочисленности и разнообразию приложений задача Дирихле занимает
исключительное место в математике. К ней непосредственно сводится основная
задача в гидродинамике – задача обтекания, задачи кручения и изгиба в теории
упругости. С нею же тесно связаны основные задачи статистической теории
упругости. Мы будем заниматься плоской задачей, которая представляет для нас
особый интерес как по обилию приложений, так и по большей разработанности и
эффективности методов решения.
2. Совокупность гармонических функций – это совокупность всех решений
уравнения Лапласа
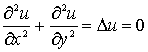 , (1)
которое является одним из простейших дифференциальных уравнений с частными
производными второго порядка.
Подобно тому, как в случае обыкновенных дифференциальных уравнений для
выделения одного определенного решения задают дополнительные условия, так и
для полного определения решения уравнения Лапласа требуются дополнительные
условия. Для уравнения Лапласа они формулируются в виде так называемых
краевых условий, т.е. заданных соотношений, которым должно удовлетворять
искомое решение на границе области.
Простейшее из таких условий сводится к заданию значений искомой гармонической
функции в каждой точке границы области. Таким образом, мы приходим к первой
краевой задаче или задаче Дирихле:
Найти гармоническую в области D и непрерывную в , (1)
которое является одним из простейших дифференциальных уравнений с частными
производными второго порядка.
Подобно тому, как в случае обыкновенных дифференциальных уравнений для
выделения одного определенного решения задают дополнительные условия, так и
для полного определения решения уравнения Лапласа требуются дополнительные
условия. Для уравнения Лапласа они формулируются в виде так называемых
краевых условий, т.е. заданных соотношений, которым должно удовлетворять
искомое решение на границе области.
Простейшее из таких условий сводится к заданию значений искомой гармонической
функции в каждой точке границы области. Таким образом, мы приходим к первой
краевой задаче или задаче Дирихле:
Найти гармоническую в области D и непрерывную в 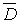 функцию u(z), которая на границе D принимает заданные
непрерывные значения u(
функцию u(z), которая на границе D принимает заданные
непрерывные значения u(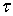 ).
К задаче Дирихле приводится еще, кроме вышеперечисленных, отыскание
температуры теплового поля или потенциала электростатического поля в
некоторой области при заданной температуре или потенциале на границе области.
К ней сводятся и краевые задачи других типов.
б) Обобщенная задача Дирихле.
В приложениях условие непрерывности граничных значений
).
К задаче Дирихле приводится еще, кроме вышеперечисленных, отыскание
температуры теплового поля или потенциала электростатического поля в
некоторой области при заданной температуре или потенциале на границе области.
К ней сводятся и краевые задачи других типов.
б) Обобщенная задача Дирихле.
В приложениях условие непрерывности граничных значений 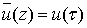 , является слишком стеснительным и приходится рассматривать обобщенную задачу
Дирихле [1]:
На границе
, является слишком стеснительным и приходится рассматривать обобщенную задачу
Дирихле [1]:
На границе 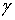 области
D задана функция области
D задана функция 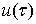 , непрерывная всюду, кроме конечного числа точек
, непрерывная всюду, кроме конечного числа точек 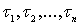 , где она имеет точки разрыва первого рода. Найти гармоническую и ограниченную в
области D функцию u(z), принимающую значения u(z) =
, где она имеет точки разрыва первого рода. Найти гармоническую и ограниченную в
области D функцию u(z), принимающую значения u(z) = 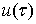 во всех точках непрерывности этой функции.
Если заданная функция
во всех точках непрерывности этой функции.
Если заданная функция 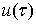 непрерывна, то обобщенная задача Дирихле совпадет с обычной, ибо условие
ограниченности функции u(z) следует из условия ее непрерывности в
непрерывна, то обобщенная задача Дирихле совпадет с обычной, ибо условие
ограниченности функции u(z) следует из условия ее непрерывности в 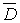 .
Теорема единственности решения обобщенной задачи Дирихле:
В данной области при заданной граничной функции
.
Теорема единственности решения обобщенной задачи Дирихле:
В данной области при заданной граничной функции 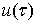 существует не более одного решения обобщенной задачи Дирихле.
Решение обобщенной задачи Дирихле можно свести к решению обычной задачи Дирихле.
Можно доказать, что:
1. для любой односвязной области D
и любой кусочно-непрерывной с точками разрыва первого рода граничной функции
существует не более одного решения обобщенной задачи Дирихле.
Решение обобщенной задачи Дирихле можно свести к решению обычной задачи Дирихле.
Можно доказать, что:
1. для любой односвязной области D
и любой кусочно-непрерывной с точками разрыва первого рода граничной функции 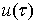 решение обобщенной задачи Дирихле существует.
2. решение обобщенной задачи Дирихле
для единичного круга дается интегралом Пуассона
решение обобщенной задачи Дирихле существует.
2. решение обобщенной задачи Дирихле
для единичного круга дается интегралом Пуассона
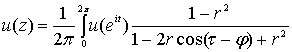 , , 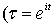 , , 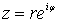 ) (2)
3. для произвольной области D,
мы получим искомую формулу для решения обобщенной задачи Дирихле интегральной
формулой Дж.Грина [12, 18]: ) (2)
3. для произвольной области D,
мы получим искомую формулу для решения обобщенной задачи Дирихле интегральной
формулой Дж.Грина [12, 18]:
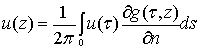 , (3)
где , (3)
где 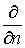 - производная в направлении внутренней нормали к С,
ds - элемент длины - производная в направлении внутренней нормали к С,
ds - элемент длины 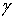 , соответствующей , соответствующей 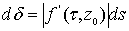 , ,
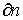 - элемент
внутренней нормали к - элемент
внутренней нормали к 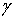 ,
, 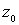 - фиксированная
произвольная точка области D, а функция - фиксированная
произвольная точка области D, а функция 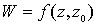 ;
; 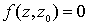 , реализующая
отображение D на единичный круг , реализующая
отображение D на единичный круг 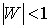 и
и 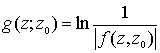 - функция Грина
для области D, гармоническую всюду в D кроме точки - функция Грина
для области D, гармоническую всюду в D кроме точки 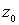 , где имеет плюс.
Формула Грина (3) выражает решение задачи Дирихле для некоторой области D
через логарифм конформного отображения D на единичный круг, т.е. сводит
решение задачи Дирихле к задаче конформного отображения. И обратное верно.
Итак, задача конформного отображения области на единичный круг и задача
Дирихле для той же области эквивалентны, они сводятся друг к другу с помощью
простых операций дифференцирования и интегрирования.
в) Видоизмененная задача Дирихле.
Пусть S+ - связная область, ограниченная простыми замкнутыми
непересекающимися гладкими контурами
, где имеет плюс.
Формула Грина (3) выражает решение задачи Дирихле для некоторой области D
через логарифм конформного отображения D на единичный круг, т.е. сводит
решение задачи Дирихле к задаче конформного отображения. И обратное верно.
Итак, задача конформного отображения области на единичный круг и задача
Дирихле для той же области эквивалентны, они сводятся друг к другу с помощью
простых операций дифференцирования и интегрирования.
в) Видоизмененная задача Дирихле.
Пусть S+ - связная область, ограниченная простыми замкнутыми
непересекающимися гладкими контурами 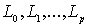 , из которых первый охватывает все остальные. Под L мы будем
подразумевать совокупность этих контуров
, из которых первый охватывает все остальные. Под L мы будем
подразумевать совокупность этих контуров 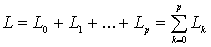 , (
, (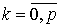 ). Через ). Через 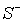 - мы обозначим совокупность конечных областей
- мы обозначим совокупность конечных областей 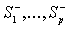 заключенных, соответственно, внутри контуров
заключенных, соответственно, внутри контуров 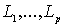 и бесконечной области
и бесконечной области 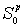 , состоящей из точек расположенных вне
, состоящей из точек расположенных вне 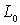 . На контуры
. На контуры 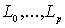 мы
наложим еще следующее условие: угол, составляемый касательной к мы
наложим еще следующее условие: угол, составляемый касательной к 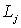 с постоянным направлением, удовлетворяет условию H; иными словами, мы
будем считать, что L удовлетворяет условию Ляпунова [17,24].
Функция
с постоянным направлением, удовлетворяет условию H; иными словами, мы
будем считать, что L удовлетворяет условию Ляпунова [17,24].
Функция 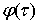 удовлетворяет условию H на этом множестве, если для любых двух
удовлетворяет условию H на этом множестве, если для любых двух 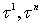 переменной
переменной 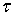 на этом
множестве на этом
множестве
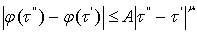 , (4)
где A и , (4)
где A и 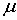 -
положительные постоянные показатели Гельдера, А – коэффициент, а -
положительные постоянные показатели Гельдера, А – коэффициент, а 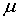 - показатель условия Н и при
- показатель условия Н и при 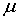 =1 – условие Липшица, функции, удовлетворяющие условию Н называются
непрерывными по Гельдеру и сильнее, чем обычное определение непрерывности.
г) Классическая задача Дирихле для многосвязных областей [24].
Найти (действительную) функцию u(x,y), гармоническую в
=1 – условие Липшица, функции, удовлетворяющие условию Н называются
непрерывными по Гельдеру и сильнее, чем обычное определение непрерывности.
г) Классическая задача Дирихле для многосвязных областей [24].
Найти (действительную) функцию u(x,y), гармоническую в 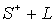 , по граничному условию
u=f(t) на L, (5)
где f(t) – заданная на L (действительная) непрерывная функция; в
случае бесконечной области от функции u(x,y) требуется еще, чтобы она
оставалась ограниченной на бесконечности, т.е. и стремится к вполне
определенному пределу, когда z уходит в бесконечность.
Напомним, что всякая функция u(z) гармоническая вне круга , по граничному условию
u=f(t) на L, (5)
где f(t) – заданная на L (действительная) непрерывная функция; в
случае бесконечной области от функции u(x,y) требуется еще, чтобы она
оставалась ограниченной на бесконечности, т.е. и стремится к вполне
определенному пределу, когда z уходит в бесконечность.
Напомним, что всякая функция u(z) гармоническая вне круга 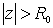 в ряд. в ряд.
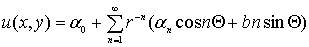 , , 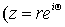 )
абсолютно и равномерно сходящийся вне круга любого радиуса )
абсолютно и равномерно сходящийся вне круга любого радиуса 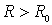 поэтому u→
поэтому u→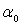 при r→
при r→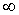 .
Для некоторых применений не меньший интерес представляет и следующая задача,
которая называется "видоизмененной задачей Дирихле". Термин этот введен в
статье Н.И.Мусхелишвили и Д.З.Авазошвили [17].
Видоизмененная задача Дирихле – задача Дирихле
для многосвязных областей.
Найти функцию u(x,y), гармоническую в S+, непрерывную в .
Для некоторых применений не меньший интерес представляет и следующая задача,
которая называется "видоизмененной задачей Дирихле". Термин этот введен в
статье Н.И.Мусхелишвили и Д.З.Авазошвили [17].
Видоизмененная задача Дирихле – задача Дирихле
для многосвязных областей.
Найти функцию u(x,y), гармоническую в S+, непрерывную в 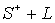 , по следующим условиям:
1. u(x,y)= , по следующим условиям:
1. u(x,y)=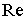 Ф(z) является действительной частью функции Ф(z), голоморфной в S+;
2. она удовлетворяет граничному условию
u=f(t)+ Ф(z) является действительной частью функции Ф(z), голоморфной в S+;
2. она удовлетворяет граничному условию
u=f(t)+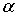 (t) на L, (6)
где f(t) – заданная на (t) на L, (6)
где f(t) – заданная на 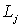 непрерывная функция непрерывная функция 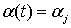 , , 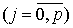 , (7)
где , (7)
где 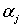 постоянные не
задаваемые заранее; в случае бесконечной области требование u(x,y)=f(t)+ постоянные не
задаваемые заранее; в случае бесконечной области требование u(x,y)=f(t)+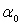 на
на 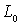 заменяются
требованием ограниченности u(x,y) на бесконечности.
Можно показать, что постоянные заменяются
требованием ограниченности u(x,y) на бесконечности.
Можно показать, что постоянные 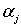 вполне определяются условиями самой задачи, если (произвольно) фиксировать одну
из них.
Если L состоит из единственного замкнутого контура, то различают два случая:
а) р=0. Тогда S+ представляет собой конечную часть
плоскости, ограниченную контуром
вполне определяются условиями самой задачи, если (произвольно) фиксировать одну
из них.
Если L состоит из единственного замкнутого контура, то различают два случая:
а) р=0. Тогда S+ представляет собой конечную часть
плоскости, ограниченную контуром 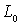 ;
б) р=1, а контур
;
б) р=1, а контур 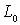 отсутствует. Тогда область S+ представляет собой бесконечную
часть плоскости, ограниченную контуром
отсутствует. Тогда область S+ представляет собой бесконечную
часть плоскости, ограниченную контуром 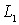 .
Легко видеть, что в случае а) задачи А и В совпадают (если
считать
.
Легко видеть, что в случае а) задачи А и В совпадают (если
считать 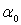 =0) в
случае б) эти задачи непосредственно сводятся одна к другой.
Каждая из задач А и В не может иметь более одного решения (если =0) в
случае б) эти задачи непосредственно сводятся одна к другой.
Каждая из задач А и В не может иметь более одного решения (если 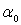 =0).
д) Общая формулировка задачи Дирихле.
Задача Дирихле – задача отыскания регулярной в области D гармонической
функции и которая на границе Г области D совпадает с наперед
заданной функцией =0).
д) Общая формулировка задачи Дирихле.
Задача Дирихле – задача отыскания регулярной в области D гармонической
функции и которая на границе Г области D совпадает с наперед
заданной функцией 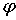 .
Задачу отыскания регулярного в области решения эллиптического уравнения 2-го
порядка, принимающего на перед заданные значения на границе области, также
называется задачей Дирихле, или первой краевой задачей.
Вопросы связанные с этой задачей, рассматривались еще К.Гауссом, а затем
Дирихле. Для областей D с достаточно гладкой границей Г решение
задачи Дирихле можно представить интегральной формулой .
Задачу отыскания регулярного в области решения эллиптического уравнения 2-го
порядка, принимающего на перед заданные значения на границе области, также
называется задачей Дирихле, или первой краевой задачей.
Вопросы связанные с этой задачей, рассматривались еще К.Гауссом, а затем
Дирихле. Для областей D с достаточно гладкой границей Г решение
задачи Дирихле можно представить интегральной формулой
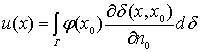 , (8)
где , (8)
где 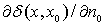 - производная
по направлению внутренней нормали в точке - производная
по направлению внутренней нормали в точке 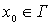 функции Грина
функции Грина 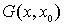 ,
характеризуемой следующими свойствами:
1. ,
характеризуемой следующими свойствами:
1. 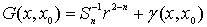 , при , при 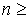 3 или 3 или
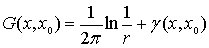 , при , при 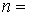 2,
где 2,
где 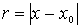 - расстояние
между точками - расстояние
между точками 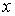 и и 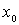 ,
, 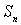 - площадь
единичной сферы в - площадь
единичной сферы в 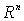 , , 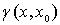 - регулярная в
- регулярная в 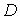 гармоническая функция как относительно координат
гармоническая функция как относительно координат 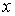 , так и относительно координат
, так и относительно координат 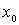 ;
2.
;
2. 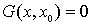 , когда , когда 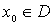 , , 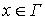 .
Для шара, полупространства и некоторых других простейших областей функция
Грина строится явно и формула (8) дает эффективное решение задачи Дирихле.
Получаемые при этом для шара и полупространства формулы носят название формул
Пуассона.
Задача Дирихле является одной из основных проблем теории потенциала – теории
гармонических функций.
Для обобщенного по Винеру решения задачи Дирихле справедливо интегральное
представление в виде формулы Вилля-Пуассона .
Для шара, полупространства и некоторых других простейших областей функция
Грина строится явно и формула (8) дает эффективное решение задачи Дирихле.
Получаемые при этом для шара и полупространства формулы носят название формул
Пуассона.
Задача Дирихле является одной из основных проблем теории потенциала – теории
гармонических функций.
Для обобщенного по Винеру решения задачи Дирихле справедливо интегральное
представление в виде формулы Вилля-Пуассона
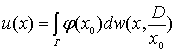 , (9)
являющейся обобщением формулы (8). Здесь , (9)
являющейся обобщением формулы (8). Здесь 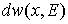 - гармоническая мера множества
- гармоническая мера множества 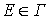 в точке
в точке 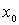 . Отсюда
возникает возможность рассмотрения обобщенной задачи Дирихле для произвольных
граничных функций . Отсюда
возникает возможность рассмотрения обобщенной задачи Дирихле для произвольных
граничных функций 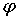 ,
при этом можно требовать удовлетворения граничного условия лишь в некоторой
ослабленной форме.
Например, если ,
при этом можно требовать удовлетворения граничного условия лишь в некоторой
ослабленной форме.
Например, если 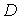 -
область -
область 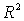 с
достаточно гладкой границей Г, а граничащая функция с
достаточно гладкой границей Г, а граничащая функция 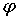 имеет только точки разрыва 1-го рода, то можно требовать удовлетворения
граничного условия лишь в точках непрерывности
имеет только точки разрыва 1-го рода, то можно требовать удовлетворения
граничного условия лишь в точках непрерывности 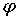 , для обеспечения единственности решения в точках разрыва требуется
ограниченность решения.
е) Задача Неймана.
Наряду с задачей Дирихле для некоторых приложений важно рассмотреть так
называемую вторую краевую задачу, или задачу Неймана:
Найти гармоническую в области
, для обеспечения единственности решения в точках разрыва требуется
ограниченность решения.
е) Задача Неймана.
Наряду с задачей Дирихле для некоторых приложений важно рассмотреть так
называемую вторую краевую задачу, или задачу Неймана:
Найти гармоническую в области 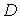 функцию
функцию 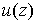 , зная
значения ее нормальной производной на границе С: , зная
значения ее нормальной производной на границе С:
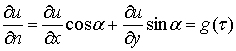 (10)
и значение (10)
и значение 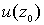 в какой-либо точке в какой-либо точке 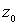 в области в области 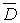 .
Для определенности мы будем предполагать, что в (10) рассматривается внешняя
нормаль, что означает угол, образованный этой нормалью с осью х.
Функция .
Для определенности мы будем предполагать, что в (10) рассматривается внешняя
нормаль, что означает угол, образованный этой нормалью с осью х.
Функция 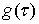 может
иметь на может
иметь на 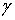 конечное
число точек разрыва 1-го рода, функция и ее частные производные первого порядка
предполагаются ограниченными.
Следующая теорема выражает от нормальной производной гармонической функции:
Если функция конечное
число точек разрыва 1-го рода, функция и ее частные производные первого порядка
предполагаются ограниченными.
Следующая теорема выражает от нормальной производной гармонической функции:
Если функция 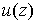 гармонична в односвязной области
гармонична в односвязной области 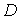 и непрерывна вместе со своими частными производными в
и непрерывна вместе со своими частными производными в 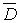 , то
, то
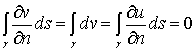 , (11)
где , (11)
где  - граница
области - граница
области 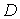 обозначает
производную в направлении нормали к обозначает
производную в направлении нормали к 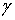 , а
, а 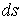 - дифференциал
дуги.
Из этой теоремы следует, что для разрешимости задачи Неймана необходимо
выполнения соотношения - дифференциал
дуги.
Из этой теоремы следует, что для разрешимости задачи Неймана необходимо
выполнения соотношения
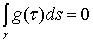 . (12)
Доказывается единственность решения задачи Неймана и при доказательстве
единственности решения задачи Неймана можно ограничиться случаем, когда область . (12)
Доказывается единственность решения задачи Неймана и при доказательстве
единственности решения задачи Неймана можно ограничиться случаем, когда область 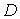 представляет собой полуплоскость (
представляет собой полуплоскость (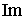 z, > 0).
В дополнительном предположении непрерывности частных производных в
z, > 0).
В дополнительном предположении непрерывности частных производных в 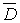 решение задачи Неймана сводится к решению задачи Дирихле для сопряженной
гармонической функции.
Две гармонические в области
решение задачи Неймана сводится к решению задачи Дирихле для сопряженной
гармонической функции.
Две гармонические в области 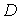 функции
функции 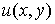 и и 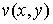 , связанные условиями Даламбера-Эйлера называются сопряженными.
Как мы знаем, для всякой функции
, связанные условиями Даламбера-Эйлера называются сопряженными.
Как мы знаем, для всякой функции 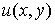 гармонической в односвязной области
гармонической в односвязной области 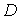 , можно найти сопряженную с ней гармоническую функцию
, можно найти сопряженную с ней гармоническую функцию 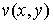 . Так как функция определяется своими частными производными с точностью до
постоянного слагаемого, то совокупность всех гармонических функций
. Так как функция определяется своими частными производными с точностью до
постоянного слагаемого, то совокупность всех гармонических функций 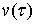 сопряженных с
сопряженных с 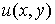 дает
формула: дает
формула:
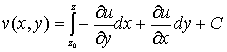 , (13)
где С – произвольная действительная постоянная.
Заметим, что в многосвязной области , (13)
где С – произвольная действительная постоянная.
Заметим, что в многосвязной области 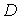 интеграл (13) по контуру
интеграл (13) по контуру 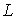 , определяет, вообще говоря, многозначную функцию:
, определяет, вообще говоря, многозначную функцию:
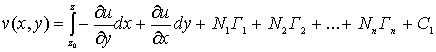 , (14)
где
, (14)
где 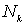 - произвольные
целые числа, а - произвольные
целые числа, а 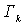 -
интегралы вдоль замкнутых контуров -
интегралы вдоль замкнутых контуров 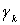 , каждый из которых содержит внутри себя одну связную часть границы
, каждый из которых содержит внутри себя одну связную часть границы 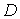 :
:
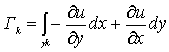 . (15)
Постоянные . (15)
Постоянные 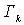 называются периодами интеграла (13) или циклическими постоянными.
Можно доказать, что решение задачи Неймана сводится к решению задачи Дирихле для
сопряженной гармонической функции называются периодами интеграла (13) или циклическими постоянными.
Можно доказать, что решение задачи Неймана сводится к решению задачи Дирихле для
сопряженной гармонической функции 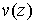 , где
, где 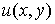 , , 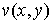 носят название соответственно силовой функции и потенциала поля.
Функции
носят название соответственно силовой функции и потенциала поля.
Функции 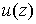 и и 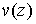 , представляющие собой регулярные решения системы Коши-Римана [6]: , представляющие собой регулярные решения системы Коши-Римана [6]:
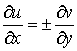 , , 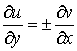 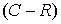 (16)
имеют частные производные всех порядков, т.е. аналитические функции (16)
имеют частные производные всех порядков, т.е. аналитические функции 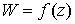 являются решением уравнения
являются решением уравнения 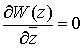 . (17)
Условие (17) – условие комплексной дифференцируемости функции
. (17)
Условие (17) – условие комплексной дифференцируемости функции 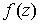 .
§2. О задачах Шварца-Пуассона.
а) Интеграл Шварца для круга .
§2. О задачах Шварца-Пуассона.
а) Интеграл Шварца для круга
|
|
|
© 2003-2013
Рефераты бесплатно, курсовые, рефераты биология, большая бибилиотека рефератов, дипломы, научные работы, рефераты право, рефераты, рефераты скачать, рефераты литература, курсовые работы, реферат, доклады, рефераты медицина, рефераты на тему, сочинения, реферат бесплатно, рефераты авиация, рефераты психология, рефераты математика, рефераты кулинария, рефераты логистика, рефераты анатомия, рефераты маркетинг, рефераты релиния, рефераты социология, рефераты менеджемент. |
|
|



