|
есть разные числа, то 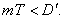
Теперь можно сделать следующий вывод:
Чуть-чуть отойдя от своей оптимальной стратегии (смотрите ниже Пример) и
таким образом почти не уменьшив свой выигрыш, Первый может значительно
уменьшить свой риск. При этом уменьшается и риск Второго, что отвечает и его
интересам.
Чисто математически можно сказать, что в описанной ситуации риск выигрыша
Первого не зависит от его стратегии непрерывно.
Рассмотрим подробно пример матричной игры с матрицей 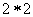
. Как известно, общий случай в окрестности оптимальных стратегий игроков
сводится к анализу такой игры.
Пример. Пусть матрица игры есть 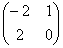
. Графическое решение этой игры показано на рисунке 1. 
Цена игры 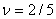 , ,
оптимальные стратегии игроков есть 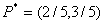
, 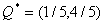 . Дисперсия . Дисперсия
выигрыша Первого при оптимальных стратегиях 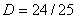
, т. е. риск игры равен примерно 1. Далее вычисления дают 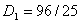
, 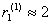 ; ; 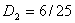
,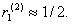 Примерная, но Примерная, но
достаточно точная зависимость риска Первого в малой окрестности его оптимальной
стратегии показана на рис. 2.
Как видно из рис. 2 при отходе Первого от своей оптимальной стратегии вправо, т.
е. при увеличении вероятности x выбора им 1-й строки. Второй начинает отвечать
1-й чистой стратегией и риск Первого скачком увеличивается до 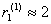
, а при отходе Первого от своей оптимальной стратегии влево Второй переходит на
свою 2-ю чистую стратегию и риск Первого скачком снижается до 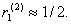
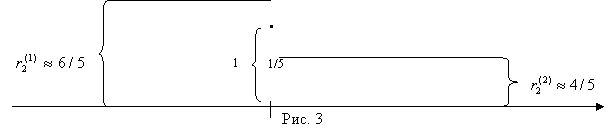
Аналогичное верно и в отношении Второго. Кратко повторим. Примерная, но
достаточно точная зависимость риска Второго в малой окрестности его оптимальной
стратегии показана на рис. 3. Как видно из рис. 3 при отходе второго от своей
оптимальной стратегии вправо, т. е. при увеличении вероятности у выбора им 1-й
строки Первый начинает отвечать 2-й чистой стратегией и риск Второго скачком
уменьшается до 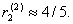 , ,
а при отходе второго от своей оптимальной стратегии влево Первый переходит на
свою 1-ю чистую стратегию и риск Второго скачком увеличивается до 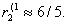
Пусть 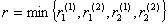 . Эту . Эту
величину и можно назвать риском всей игры. Однако играть с таким риском можно
лишь при согласии обеих сторон. Для анализируемой игры 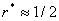
и игроки для достижения такого риска должны играть так: Первый играет со своей
оптимальной стратегией 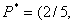
3,5), а Второй должен использовать 2-ю чистую стратегию.
§12. Анализ доходности и риска финансовых операций
Финансовой называется операция, начальное и конечное состояния которой имеют
денежную оценку и цель проведения которой заключается в максимизации дохода -
разности между конечной и начальной оценками.
Почти всегда финансовые операции проводятся в условиях неопределенности и
потому их результат невозможно предсказать заранее. Поэтому финансовые
операции рискованны, т.е. при их проведении возможны как прибыль так и убыток
(или не очень большая прибыль по сравнению с той, на что надеялись
проводившие эту операцию).
Как оценить операцию с точки зрения ее доходности и риска?
Существует несколько разных способов. Наиболее распространенным является
представление дохода операции как случайной величины и оценка риска операции
как среднего квадратического отклонения этого случайного дохода.
Рассмотрим какую-нибудь операцию, доход которой есть случайная величина Q.
Средний ожидаемый доход `Q - это математическое ожидание с.в. Q: 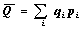
, где pi есть вероятность получить доход qi. А среднее
квадратическое отклонение (СКО) 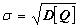
- это мера разбросанности возможных значений дохода вокруг среднего ожидаемого
дохода. Вполне разумно считать s количественной мерой риска операции и
обозначить r. Напомним, что дисперсия
D[Q] = M [(Q - `Q)2] = M [Q2] - `Q2.
Рассмотрим четыре операции Q1, Q2, Q3, Q,4
. Найдем средние ожидаемые доходы `Qi и риски ri операций.
Ряды распределения, средние ожидаемые доходы и риски:
Q1 | : | 5 | 2 | 8 | 4 | `Q1 = 29/6 »4.81 | r1 » 1.77 | | | 1/2 | 1/6 | 1/6 | 1/6 | | | | | | | | | | | Q2 | : | 2 | 3 | 4 | 12 | `Q2 = 25/6 »4.16 | r2 » 3.57 | | | 1/2 | 1/6 | 1/6 | 1/6 | | | | | | | | | | | | | | | | | | | Q3 | : | 8 | 5 | 3 | 10 | `Q3 = 7 | r3 » 2.30 | | | 1/2 | 1/6 | 1/6 | 1/6 | | | | | | | | | | | Q4 | : | 1 | 4 | 2 | 8 | `Q4 = 17/6 »2.81 | r4 » 2.54 | | | 1/2 | 1/6 | 1/6 | 1/6 | | |
Напомним, как находить `Q и r.
`Q1 =å qipi = 5*1/2+2*1/6+8*1/6+4*1/6=29/6
j
r1 = M [Q21 ] - (Q1)2; M [Q21] = 25*1/2+4*1/6+64*1/6+16*1/6=159/6;
Q21 = 841/36; D [Q1] = (159*6-841)/36 = 113/36; 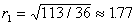
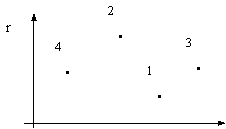 Нанесем средние ожидаемые Нанесем средние ожидаемые
доходы `Q и риски r на плоскость - доход откладываем по горизонтали, а риски по
вертикали (см. рис.):
Получили 4 точки. Чем правее точка (`Q, r), тем более доходная операция, чем
точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и
ниже. Точка (`Q¢, r¢) доминирует точку (`Q, r) если `Q¢ ³`Q
и r¢ £ r. В нашем случае 1-я операция доминирует 2-ю, 3-я
доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы -
доходность 3-й больше, но и риск ее тоже больше.
Точка, не доминируемая никакой другой называется оптимальной по Парето, а
множество всех таких точек называется множеством оптимальности по Парето.
Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее
обязательно надо выбрать из операций, оптимальных по Парето.
Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу,
которая для пар (`Q, r) дает одно число, по которому и определяют лучшую
операцию. Например, пусть взвешивающая формула есть j (Q)= 2×Q - r .
Тогда получаем:
j (Q1)= 2*4.81-1.77 = 7.85; j (Q2)= 4.75; j (Q3)= 11.70; j (Q4)= 3.08
Видно, что 3-я операция - лучшая, а 4-я - худшая.
§13. Задача формирования оптимального
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
| 


