|
y2 (2x1 +5x2 + 2x
4 - 107) = 0
x 3 (4y1 + 2y3 - 25) = 0
y3 (3x1 + x2 + 2x3 +
5x4 - 181) = 0 .
x 4(5y1 + 2y2 + 5y3 - 50) = 0
Ранее было найдено, что в решении исходной задачи х1>0, x4>0. Поэтому
4y1 + 2y2 + 3y3 - 36 = 0
5y1 + 2y2 + 5y3 - 50 = 0
Если же учесть, что второй ресурс был избыточным и, согласно той же теореме
двойственности, ее двойственная оценка равна нулю
у2=0,
то приходим к системе уравнений
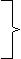 4y1 + 3y3 - 36 = 0 4y1 + 3y3 - 36 = 0
5y1 + 5y3 - 50 = 0
откуда следует
у1=6, у3=4.
Таким образом, получили двойственные оценки ресурсов
у1=6; у2=0; у3=4,
(4)
причем общая оценка всех ресурсов равна 1972.
Заметим, что решение (4) содержалось в последней строке последней симплексной
таблицы исходной задачи. Важен экономический смысл двойственных оценок.
Например, двойственная оценка третьего ресурса у3=4 показывает, что
добавление одной единицы третьего ресурса обеспечит прирост прибыли в 4
единицы.
§6. Задача о "расшивке узких мест производства"
При выполнении оптимальной производственной программы первый и третий ресурсы
используются полностью, т.е. образуют ²узкие места производства².
Будем их заказывать дополнительно. Пусть T(t1,t2,t3
)- вектор дополнительных объемов ресурсов. Так как мы будем использовать
найденные двойственные оценки ресурсов, то должно выполняться условие
H + Q-1T 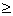 0. 0.
Задача состоит в том, чтобы найти вектор
T (t1, 0, t3),
максимизирующий суммарный прирост прибыли
W = 6t1 + 4t3
(1)
при условии сохранения двойственных оценок ресурсов (и, следовательно,
структуры производственной программы)

предполагая, что можно надеяться получить
дополнительно не более 1/3 первоначального объема ресурса каждого вида
 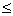 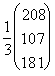 (3) (3)
причем по смыслу задачи
t1 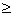 0, t3 0, t3 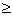 0. (4) 0. (4)
 Переписав неравенства (2) и (3) в виде: Переписав неравенства (2) и (3) в виде:
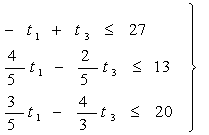
приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).
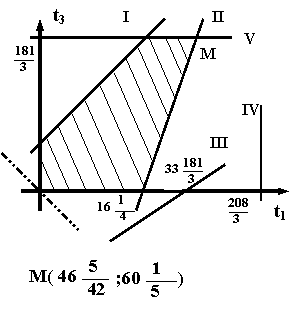
Эту задачу легко решить графически: см. рис. 1. Программа
²расшивки² имеет вид
t1=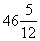 , t2=0, t3= , t2=0, t3=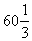
и прирост прибыли составит 519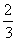 . .
Сводка результатов приведена в таблице
Таблица 1
сj | 36 | 14 | 25 | 50 | b | x4+i | yi | ti | | 4 | 3 | 4 | 5 | 208 | 0 | 6 | 46 5/12 | aij | 2 | 5 | 0 | 2 | 107 | 13 | 0 | 0 | | 3 | 1 | 2 | 5 | 181 | 0 | 4 | 60 1/3 | | xj | 27 | 0 | 0 | 20 | 1972 | | | 519 2/3 | Dj | 0 | 8 | 7 | 0 | | | | |
§7. Транспортная задача линейного программирования
Транспортная задача формулируется следующим образом. Однородный продукт,
сосредоточенный в m пунктах производства (хранения) в количествах а
1, а2,..., аm единиц, необходимо распределить между
n пунктами потребления, которым необходимо соответственно b1, b
2,..., bn единиц. Стоимость перевозки единицы продукта из i-го
пункта отправления в j-ый пункт назначения равна сij и известна для
всех маршрутов. Необходимо составить план перевозок, при котором запросы всех
пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах
производства и общие транспортные расходы по доставке продуктов были
минимальными.
Обозначим через хij количество груза, планируемого к перевозке от
i-го поставщика j-му потребителю. При наличии баланса производства и
потребления
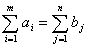 (1) (1)
математическая модель транспортной задачи будет выглядеть так:
найти план перевозок
Х = (хij), i = 1,m; j = 1,n
минимизирующий общую стоимость всех перевозок
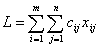 (2) (2)
при условии, что из любого пункта производства вывозится весь продукт
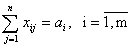 (3) (3)
и любому потребителю доставляется необходимое количество груза
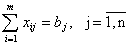 (4) (4)
причем по смыслу задачи
х11 > 0 ,. . . ., xmn > 0.
(5)
Для решения транспортной задачи чаще всего применяется метод потенциалов
. Пусть исходные данные задачи имеют вид
А(а1, а2, а3) = (54; 60; 63); В(b1
, b2, b3, b4) = (41; 50; 44; 30); С = 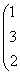 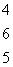 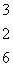  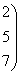
Общий объем производства åаi = 55+60+63 = 178 больше, требуется
всем потребителям åbi = 42+50+44+30 = 166, т.е. имеем открытую
модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный
пункт потребления с объемом потребления 178-166 = 12 единиц, причем тарифы на
перевозку в этот пункт условимся считать равными нулю, помня, что переменные,
добавляемые к левым частям неравенств для превращения их в уравнения, входят в
функцию цели с нулевыми коэффициентами.
Первое базисное допустимое решение легко построить по правилу ²северо-
западного угла².
 Потребление Потребление
| b1 =41 | b2 =50 | b3 =44 | b4 =30 | b5 =12 | |  Производство Производство
| | | | | | | а1 =54 | 41 | 13 | | | | p1 =0 | a2 =60 | | 37 | 23 | | | p2 = | a3 =63 | * | | 21 | 30 | 12 | p3 = | | q1 = | q2 = | q3 = | q4 = | q5 = | |
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
| 


