|
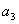 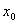 + +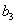 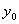 + +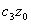 = = 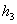 . .
Вычитая почленно из уравнений (3.19) тождества (3.34), получим систему уравнений
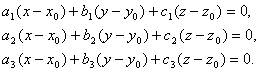
эквивалентную системе (3.19). Но система (3.35) является однородной
системой трех линейных уравнений относительно трех неизвестных 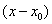
, 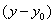 и и 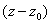
с определителем 
, равным нулю. Согласно разд. 2.3 последняя система (а стало быть, и система
(3.19)) имеет бесчисленное множество решений. Например, в случае, когда отличен
от нуля минор (3.27), мы с помощью формул (3.31) получим следующее бесконечное
множество решений системы (3.19):
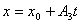 , , 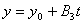 , , 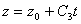
(t принимает любые значения).
Сформулированное утверждение доказано, и мы можем сделать следующее заключение:
если  = = 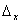
= 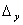 = = 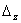
= 0, то неоднородная система уравнений (3.19) либо совсем не имеет решений,
либо имеет их бесконечное множество.
3. Понятие об определителях любого порядка и о линейных системах с
любым числом неизвестных
Установленное нами свойство разложения определителя третьего порядка до
элементам любой (например, первой) строки может быть положено в основу
последовательного введения по индукции определителя четвертого, пятого и всех
последующих порядков.
Предположим, что нами уже введено понятие определителя порядка (n-1), и
рассмотрим произвольную квадратную матрицу состоящую из 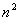
элементов
  
Назовем минором любого элемента 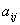
матрицы (3.36) уже введенный нами определитель порядка (n-1), отвечающий матрице
(3.36), у которой удалены i-я строка и j-й столбец. Договоримся обозначать
минор элемента 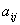
символом 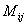 . .
Например, минор любого элемента 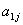
первой строки матрицы (3.36) является следующим определителем порядка (n-1):
Назовем определителем порядка n, отвечающим матрице (3.36), число 
, равное сумме
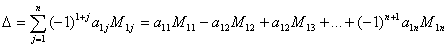
и обозначаемое символом
 = = 
Заметим, что при n = 3 разложение (3.37) совпадает с разложением (3.16)
определителя третьего порядка по первой строке.
Рассмотрим теперь неоднородную систему n уравнений с n неизвестными:
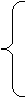 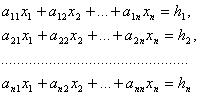
Определитель порядка n, составленный из коэффициентов при неизвестных системы
(3.39) и совпадающий с определителем 
из равенства (3.38), называется определителем этой системы При любом j, равном
1, 2, ..., n, обозначим символом 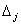
определитель порядка n, полученный из определителя системы 
путем замены его j-го столбца столбцом свободных членов 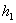
, 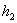 , ..., , ..., 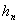
.
В полной аналогии со случаем n = 3 оказывается справедлив следующий результат:
если определитель 
неоднородной системы (3.39) отличен от нуля, то эта система имеет единственное
решение, определяемое формулами Крамера:
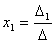 , , 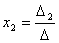 , , 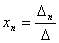 . .
Далее можно доказать, что если определитель системы 
равен нулю, а хотя бы один из определителей 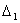
, 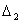 , ..., , ..., 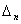
отличен от нуля, то система (3.39) не имеет решений.
В случае же, если n > 2 и все определители 
, 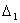 , , 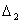
, ..., 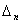 , равны нулю, , равны нулю,
система (3.39) может также не иметь решений, но если она имеет хотя бы одно
решение, то она имеет их бесчисленное множество.
4. Отыскание решения линейной системы методом Гаусса
Рассмотрим неоднородную систему (3.39), в которой мы теперь для сокращения
записи переобозначим свободные члены 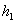
, 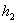 , ..., , ..., 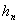
, используя для них обозначение 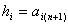
при i = 1, 2 ..., n. Изложим один из самых простых методов решения этой системы,
заключающийся в последовательном исключении неизвестных и называемый
методом Гаусса.
Выберем из коэффициентов 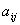
при неизвестных коэффициент, отличный от нуля, и назовем его ведущим. Не
ограничивая общности, будем считать, что таким коэффициентом является 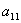
(иначе мы могли бы поменять порядок следования неизвестных и уравнений).
Поделив все члены первою уравнения (3.39) на 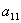
, получим первое приведенное уравнение
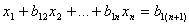
в котором 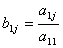 при j = 1, 2, ..., (n+1). при j = 1, 2, ..., (n+1).
Напомним, что 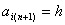 , и, в частности, , и, в частности, 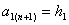 . .
Для исключения неизвестного 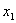 вычтем из i-го уравнения системы (3.39) вычтем из i-го уравнения системы (3.39)
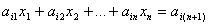 (i = 2, 3 ..., n) (i = 2, 3 ..., n)
умноженное на 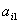 приведенное уравнение (3.40). приведенное уравнение (3.40).
В результате получим для любого i = 2, 3, ..., n уравнение
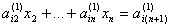 , ,
в котором
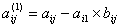 при j = 2, 3, ..., (n+1). при j = 2, 3, ..., (n+1).
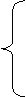 Таким образом, мы получаем первую укороченную систему: Таким образом, мы получаем первую укороченную систему:
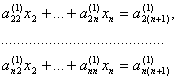
коэффициенты которой определяются по формулам (3.41).
В системе (3.42) находим отличный от нуля ведущий коэффициент. Пусть это будет 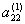
. Тогда, поделив первое уравнение (3.42) на этот
коэффициент, мы получим второе приведенное уравнение и, исключив с помощью этого
уравнения по описанной выше схеме неизвестное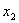
, придем ко второй укороченной системе, не содержащей 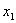
и 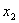 . .
 Продолжая рассуждения по этой Продолжая рассуждения по этой
схеме, называемой прямым ходом метода Гаусса, мы либо завершим ее
реализацию, дойдя до линейного уравнения, содержащего только одно неизвестное,
либо не сможем завершить ее реализацию (вследствие того, что исходная система
(3.39) не имеет решений). В случае, если исходная система (3.39) имеет решения,
мы получим цепочку приведенных уравнений
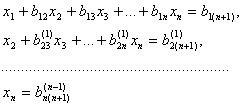
из которой обратным xодом метода Гаусса последовательно находятся неизвестные
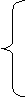 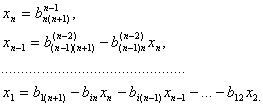
Подчеркнем, что все операции при обратном ходе метода Гаусса (1.43)
выполняются без деления,
В качестве примера рассмотрим неоднородную систему трех уравнений с тремя
неизвестными
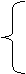
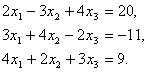
Конечно, можно убедиться в том, что определитель системы (3.44) отличен от нуля,
и найти 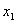 , , 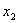
и 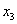 по формулам по формулам
Крамера, но мы применим метод Гаусса.
Поделив первое уравнение системы (3.44) на 2, получим первое приведенное
уравнение:
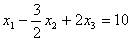 . .
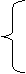 Вычитая из второго Вычитая из второго
уравнения системы (3.44) приведенное уравнение (3.45), умноженное на 3, и
вычитая из третьего уравнения системы (3.44) приведенное уравнение (3.45),
умноженное на 4, мы получим укороченную систему двух уравнений с двумя
неизвестными:
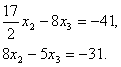
Поделив первое уравнение (3.46) на 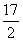 , получим второе приведенное уравнение: , получим второе приведенное уравнение:
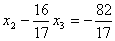 . .
Вычитая из второго уравнения (3.46) приведенное уравнение (3.47), умноженное
на 8, получим уравнение:
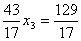 , ,
которое после сокращения на 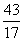 дает дает 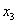 = 3. = 3.
Подставляя это значение 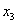
во второе приведенное уравнение (3.47), получим, что 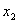
= -2. Наконец, подставляя найденные значения 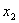
= -2 и 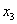 = 3 в первое = 3 в первое
приведенное уравнение (3.45), получим, что 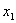
= 1.
ЛИТЕРАТУРА
1. Ильин В.А., Куркина А.В. – «Высшая математика», М.:ТК Велби, изд-во
Проспект, 2004г. – 600с.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
| 


