|
21ух + а22 у2 + a13xz + a31
zx + a23 yz + a32 zy + a22z2 .

называется матрицей квадратичной формы. Квадратичная форма имеет канонический
вид, если она содержит члены только с квадратами переменных, т.е. аij
= 0; i,j = 1,3; i≠ j . Матрица (1.6.2) квадратичной формы
(1.6.1) будет иметь диагональный вид, если в трехмерном пространстве перейти к.
новому базису, состоящему из собственных векторов (см. тему 1.5) матрицы
А, при этом на главной диагонали будут стоять собственные числа матрицы
А.
Квадратичная форма в новом базисе будет иметь вид
F(x1, y1, z1)=λ1x1
2 + λ2 y12 + λ
3z12
(1.6.3)
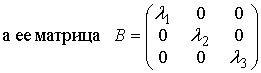
В случае двух переменных х, у квадратичная форма F(x,y) имеет вид
F(х,у) = а11х2 + 2а12 ху + а22
y2,
(1.6.4)

причем а12 = a21 .
Методы приведения квадратичной формы к каноническому виду применяются при
решении задач на приведение к каноническому виду уравнений кривых второго
порядка
a11x2 + 2а12 ху + а22 у2 + b1х + b2 y + с = 0
и уравнений поверхностей второго порядка
a11x2 + 2а12 ху + а22 у2 + 2a13 xz+2a23 yz+a22 z2 +b1х + b2 y +b3 z + с = 0
Канонические уравнения основных кривых второго' порядка были рассмотрены в
теме 1.4 (1.4.6)
Поверхности второго порядка делятся на центральные и нецентральные.
Канонические уравнения некоторых поверхностей второго порядка приведены ниже.
Уравнения центральных поверхностей второго порядка

λ=0-точка
λ =1-эллипс,
λ.=-1-мнимый эллипс.

λ =1-однополостный гиперболоид
λ =-1-двуполостный гиперболоид;
λ =0 эллиптический конус.
Нецентральные поверхности

λ =l-эллиптический параболоид,
λ =-1 гиперболический параболоид.
2.Цилиндрические поверхности:

λ=1- эллиптический цилиндр,
λ=1- гиперболический цилиндр.

-мнимый эллиптический цилиндр(уравнению не удовлетворяет ни одна точка),

-пара плоскостей,
г) х2 = 2ру, у2 = 2рх, z2 = 2рх , (1.6.12)
и т.д. параболические цилиндры .
Плоскости
х2 = λа2 , а ≠0, λ=1 пара параллельных плоскостей;
λ=-1 мнимые плоскости (уравнению не удовлетворяет ни одна точка
пространства);
λ=0 - пара совпадающих плоскостей.
Пример 1.6.1. Записать каноническое уравнение кривой второго порядка Зх2
+4xу - 4х- 8y = 0 (сравните с решением примера 1.4.1 темы 1.4).
Квадратичная форма, содержащаяся среди слагаемых левой части уравнения имеет
вид F(x,y)= Зх2+ 4xy , а ее матрица
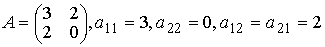
Вычислим собственные числа и собственные векторы матрицы А (см.
тему 1.5)
 Пусть собственные векторы Х Пусть собственные векторы Х
i(а1(i), а2(i)) i.=1,2,
где а1(i), а2(i -
координаты. Система (1.5.5) для нахождения собственных векторов имеет вид
(3-λ)a1+2a2=0
2a1-λa2=0
(1.6.14)
Найдем собственные числа λ , решив характеристическое уравнение (1.5.6) .
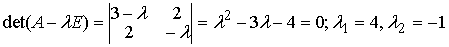
Подставим первое собственное число λ1=4 в систему
(1.6.4).
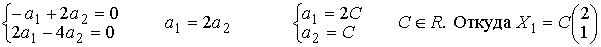
и соответствующий единичный вектор X10 имеет вид
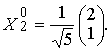
Подставим второе собственное число λ2=-1 в систему (1.6.14):
Перейдем в двумерное пространство R2 к новому базису составленному
из собственных векторов матрицы А Х10 и Х
20. При этом матрица квадратичной формы В в новом
базисе будет иметь вид (1.5.3)
где матрица Т составлена из координат собственных векторов, записанных в
столбцы. Связь между старыми координатами х, у (в базисе i,
j ) и новыми координатами x1, y1 (в новом базисе)
реализуется по формуле
квадратичная форма в новом базисе имеет вид (1.6.3) (случай двух переменных)
F(x1, y1) = 4x12 - у1
2 .
Запишем равнение кривой второго порядка в новых координатах, приведем подобные.
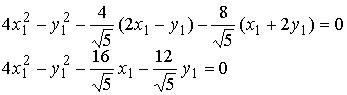
Уравнение совпало с уравнением, полученным в примере 1.4.1. темы 1.4 и
поэтому дальнейшие преобразования идентичны.
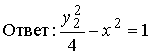
сопряженная гипербола с полуосями а=1, b=2.
Пример 1.6.2.Записать каноническое уравнение поверхности второго порядка
11x2 + 4ху + 2y2 - 16xz + 20yz + 5z2 + 6x + l2y -6=0.
Запишем квадратичную форму, входящую в состав левой части уравнения
F(x,y,z)=llxг + 4ху+2у2 - 16xz + 20yz + 5z2
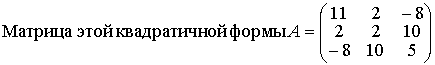
Собственные числа этой матрицы λ1 = 9, λ2 = l8,
λ 3 = -9 и единичные cобст-венные векторы X10
= (2/3, 2/3, 1/3)T, X20 =(-2/3, 1/3, 2/3)Т
, X30=(1/3, -2/3, 2/3)Т
найдены в примере 1.5.4 (см. тему 1.5). Связь между координатами x, y,z в
старом базисе (i,j,k) и координатами x1,y1,z
1 в новом базисе (X10,X20
,X30) имеет вид
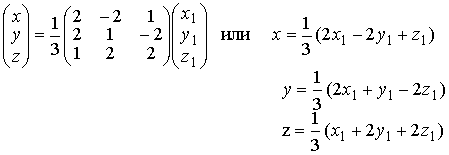
Выше записанная матрица, как в примере 1.6.1,образована из координат
собственных векторов, записанных в столбцы. Матрица квадратичной формы В
в новом базисе - диагональная
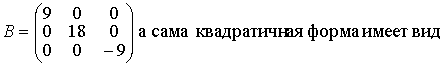
F(x,y,z) =9x12 +18y12 -9z12
Запишем уравнение поверхности второго порядка в новых координатах, приведем
подобные члены и выделим полные квадраты
9x12 +18y1 2 - 9z12 + 2(2x1 - 2y1 + z1) + 4(2x1 +y1 -2z1) - б = 0;
9x12 + I8y12 - 9z12 +12x1 - бz1 - б = 0;
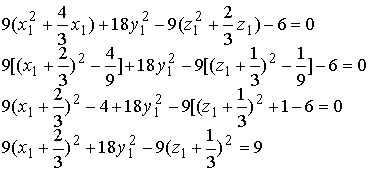
Перейдем к новым координатам (параллельный перенос)
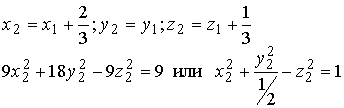
Полученное уравнение является каноническим уравнением однополо стного
гиперболоида (1.6.7) с параметрами а =1, b =√2/2, с=1.
После изучения материала, содержащегося в разделе 1, студент должен выполнить
контрольную работу N1.
Вопросы для самопроверки
1. Изобразите схематично основные поверхности второго порядка.
2. Может ли алгебраическая поверхность второго порядка представлять собою:
а) плоскость;
б) пустое множество?
Привести примеры.
3. Назовите типы и выпишите канонические уравнения цилиндрических
поверхностей второго порядка.
4.Докажите, что всякое уравнение F(x,y,z)=0, где F-однородный
многочлен второй степени, определяет конус с вершиной в начале координат .
После изучения тем 1.1-1.6 раздела 1 студенту необходимо выполнить
контрольную работу N1.
Дополнение 1.1.Образец выполнения и оформления контрольной работы N1
"Векторная алгебра и аналитическая геометрия. Матрицы. Элементы линейной
алгебры."
Задача N1.Вычислить :
a) |m+2n| ;
б) угол между векторами т+ п и -m+ п , если |т|= 2 ,|п| = 3 , (т,п)=60 o .
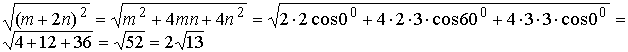
а)Согласно определения модуля |т+2п| =
б) угол между векторами a и b вычисляется по формулам
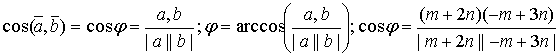
Вычислим отдельно числитель и знаменатель
(т+2n)(-m+3n)=-m2+mn+6n2 = -2∙2
+2∙3-cos60°+6∙3∙3= -4+3+36 =35;
|m+2n| =2√13 (см. пункт а) ;
Задача N2.Заданы координаты четырех вершин пирамиды ABCD .
А(-2,0,0), B(1,1,-1), С(-1,3,0), D(-1,0,2).
Вычислить АВ; (АВ,АС); площадь ΔAВС, объем пирамиды;
длину высоты DH пирамиды, проведенной к плоскости грани АВС.
Записать уравнения: прямой АВ; плоскости АВС; высоты пирамиды
DH; медианы AM треугольника АВС, высоты АК
треугольника АВС, биссектрисы AL треугольника АВС .
1. Вектор АВ имеет координаты: АВ (3,1,-1) . Поэтому его длина
равна: АВ= √9+l+l = √11 (ед) .
2.Угол φ между векторами АВ и АС определяется по формуле
(1.2.3).Вычислим длину вектора ВС :
BC=√4+4+1= 3 (ед) .
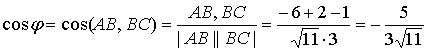
Скалярное произведение вычислялось по формуле (1.2.5)
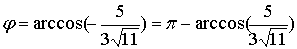
3.Площадь треугольника АВС вычислена в примере 1.2.9.
4.Объем пирамиды ABCD вычислен в примере 1.2.10
5.Длина высоты DH пирамиды, проведенной из вершины D к
грани АВС также вычислена в примере 1.2.10.
6.Уравнение прямой АВ будем искать в виде (1.3.8), т.к. заданы
две точки этой прямой А и В.
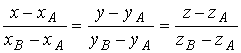
Подставляя в последнее уравнение координаты точек А и В, получим (x+2)/3=y=-z
7.Уравнение плоскости АВС можно записать в виде (1.3.4), т.к.
заданы координаты тpeх точек А,В,С
Уравнение плоскости АВС: 3x- y-8z+6 =0
8.Уравнение высоты пирамиды DH ищем в виде (1.3.6)
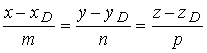
Координаты точки D известны/ а направляющий вектор прямой а(т,п,р)
коллинеарен вектору нормали к плоскости АВС . Вектор нормали к
плоскости АВС N имеет координаты N(3,-1,8)
(см. пункт 7 данной задачи). Поэтому уравнение прямой DH имеет вид
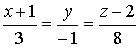
9. Уравнение медианы AM ищем в виде (1.3.8)
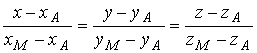
Точка М- середина отрезка В С имеет координаты
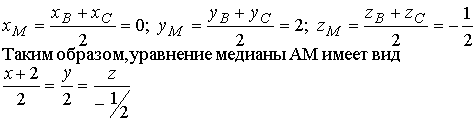
10. Уравнение высоты АК ищем в виде

Направляющий вектор прямой АК, вектор a(m,n,p) перпендикулярен
вектору N(3,-1,8)-нормали к плоскости АВС и вектору BС(-2,2,1)
(рис.Д.1.1). Поэтому вектор а может быть вычислен по формуле (1.2.10)
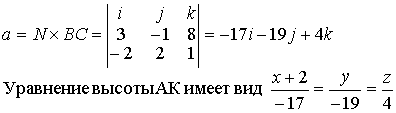
11.Точка L-точка пересечения биссектрисы AL со стороной ВС
делит отрезок ВС на части, длины которых пропорциональны длинам
прилежащих сторон, т.е.
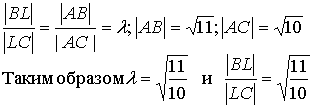
По формулам деления отрезка в данном отношении находим координаты точки L
Уравнение биссектрисы AL ищем в виде (1.3.8)
Подставляя в последнее уравнение координаты точек А и L, получим
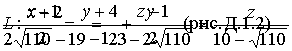
Задача N3.Составить уравнение плоскости, проходящей через точку М (3,-1,2) и
прямую
Рис.Д.1.2
Уравнение искомой плоскости ищем в виде (1.3.1)
А(х-x0 ) +B(y-y0 )+C(z-z0 )= 0 , где (x0, у0, z0) координаты точки M0(1,-4,1),
расположенной на прямой L и принадлежащей плоскости Р .
 
Вектор нормали п к плоскости Р определим из условия n = М0
М1 x а , где М0М1 (2,3,1),
а (2, -1, 2 ) .
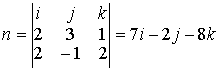
Таким образом п(А,В,С) = n(7,-2,-8) и уравнение плоскости имеет вид
7(х-1)-2(y+4)-8(z-1)=0
7х-2y-8z-7=0
Задача N4.Найти расстояние между прямыми
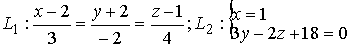
Прямая L1, проходит через точку M1(2,-2,1) и имеет направляющий вектор
a1 (3,-2,4). Уравнение прямой L2 запишем в виде
(1.3.8), предварительно определив какие-либо две точки, например: К1
(1,-6,0) и K2(1,0,9):
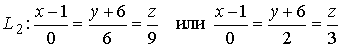
Направляющий вектор прямой L2 a2 (0,2,3). Прямые L
1 и L2 не параллельны, т.к. a1≠λa
2 , "λÎR. Проверим пересекаются ли прямые L1, и
L2 использовав условие (1.3.18)
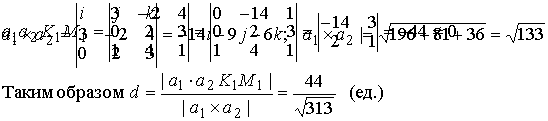
Смешанное произведение векторов отлично от нуля, поэтому прямые L1, и
L2 не пересекаются, а являются скрещивающимися прямыми. Расстояние
между скрещивающимися прямыми находим по формуле (1.3.20), предварительно
вычислив |a1 x a2| по формулам (1.2.10)
и (1.2.6)
Задача N5.Вычислить значение многочлена f(A) от матрицы А, если
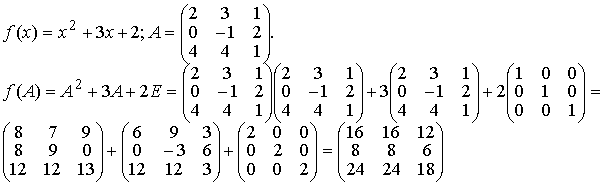
Задача N6.Матричным методом решить систему линейных алгебраическиx уравнений.
 x1+2x2+4x3=17 x1+2x2+4x3=17
x1+x2+6x3=21
2x1+3x2+3x3=17
Решение системы находим по формуле (1.1.8) X= А-1В, где
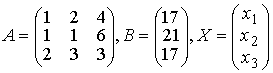
а обратная матрица вычисляется по формуле (1.1.6) .
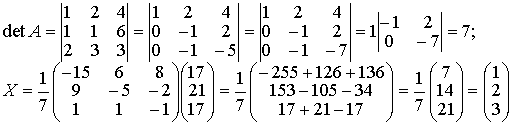
Таким образом, x1 = 1, x2 = 2, x3 = 3
Задача N7. Привести к каноническому виду уравнение линии второго порядка Зx
2 + 4xy - 4х- 8y = 0 .
Определить тип кривой.
Решение задачи приведено в примерах 1.4.1 и 1.6.1.
Метод решения студент выбирает сам.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
| 


