|
Вычислим определитель матрицы А
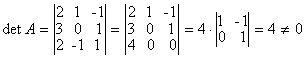
По формуле (1.1.6) находим (вычисление алгебраических дополнений элементов
матрицы А рассмотрено в примере 1.1.6) :
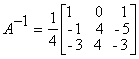
Проверка :
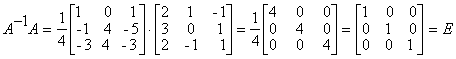
Студентам рекомендуется провести вычисление обратной матрицы методом
элементарных преобразований.
Рангом матрицы А размерности тхп называется наибольший из
порядков её миноров, отличных от нуля. Если ранг матрицы A равен r,
то это означает, что в матрице А имеется отличный от нуля минор порядка
r , но всякий минор порядка большего, чем r, равен 0.
Ранг матрицы обозначается r(А) .
Свойства ранга матрицы А размерности т´ п
1) 0 ≤ r ≤ rnin(m,n);
2) r =0 тогда и только тогда, когда матрица нулевая;
3) для квадратной матрицы n-го порядка r=n тогда и только тогда, когда
матрица невырожденная;
4) ранг транспонированной матрицы равен рангу исходной матрицы;
5) ранг матрицы не изменится, если вычеркнуть (дописать) нулевую строку
(столбец);
6) ранг матрицы не изменится, если к элементам строки матрицы прибавить
элементы другой строки матрицы, предварительно умноженные на некоторое число;
7) ранг матрицы не изменится, если переставить любые строки (столбцы) матрицы.
Пример 1.1.9. Найти ранг матрицы А

RgA=2 т.к. имеется отличный от нуля определитель второго порядка,
например
Студент должен уметь решать системы линейных алгебраических уравнений (в
дальнейшем СЛАУ)
1) по формулам Крамера и матричным методом (в случае, когда матрица
А системы невырожденная) ;
2) произвольные СЛАУ с использованием теоремы Кронекера-Капелли методом Гаусса.
Рассмотрим примеры на применение этих методов.
1) Предположим СЛАУ имеет невырожденную матрицу порядка п.
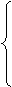 a11x1 + a12x2 + ... + a1nxn = b1 a11x1 + a12x2 + ... + a1nxn = b1
a21x1 + a22x2 + ... + a2nxn = b2
... ... ... ...
an1x1 + an2x2 + ... + annxn = bn
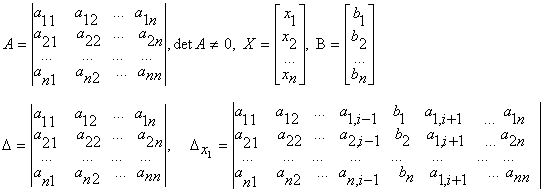
Правило Крамера. Если главный определитель СЛАУ отличен от нуля
(∆≠O), то СЛАУ имеет единственное решение, которое находится по
формулам

Матричный метод. Если матрица СЛАУ невырожденная, то решение СЛАУ может
быть найдено по формуле
X = A-1B
(1.1.8)
где матрица А-1 вычисляется по формуле (1.1.6 ), либо методом
элементарных преобразований.
Пример 1.1.10. Решить СЛАУ
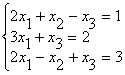
а) по формулам Крамера;
б) методом обратной матрицы
Запишем матрицу системы А, матрицу-столбец неизвестных X и
матрицу-столбец свободных членoв Х :
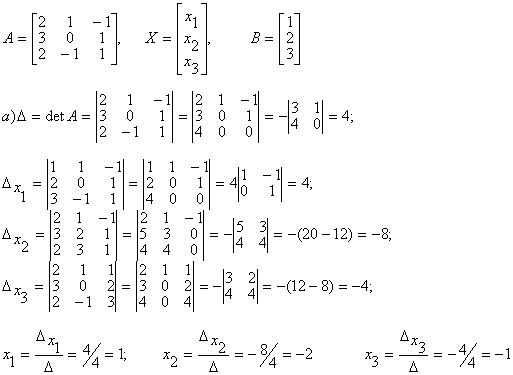
б)Воспользуемся формулой Х =А-1В, где матрица A-1 вычислена в примере 1.1.9.
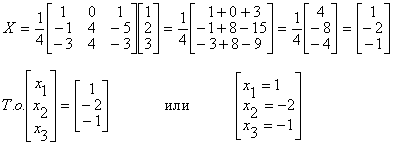
2) Предположим, что матрица СЛАУ имеет размерность mxn. В этом случае СЛАУ
имеет вид
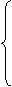 a11x1+a12x2+...+a1nxn=b1 a11x1+a12x2+...+a1nxn=b1
a21x1+a22x2+...+a2nxn=b2
... ... ... ...
am1x1+am2x2+...+amnxn=bm __
Запишем расширенную матрицу системы А.

Теорема Кронекера-Капелли. Система линейных .алгебраических уравнений
совместна тогда и только тогда, когда ранг расширенной матрицы системы равен
рангу матрицы системы.
Для решения произвольных СЛАУ применяется метод Гаусса. Сущность метода
состоит в том, что расширенная матрица СЛАУ приводится
к ступенчатому виду.
Пример 1.1.11. Решить систему
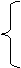 x1+7x2+3x3+2x4=6 x1+7x2+3x3+2x4=6
2x1+5x2+2x3+3x4=4
7x1+4x2+x3+9x4=2
В этой системе m=3 - количество уравнений; n=4 - количество неизвестных.
Запишем расширенную матрицу системы А и преобразуем ее к ступенчатому виду
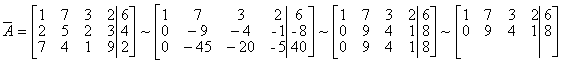
_
RgA=2, rgA=2. По теореме Кронекера-Капелли СЛАУ совместна. Укороченная
СЛАУ имеет вид:
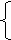 x1+7x2+3x3+2x4=6 x1+7x2+3x3+2x4=6
9x2+4x3+x4=8
В качестве базисных неизвестных выберем неизвестные х1 и x
2, а неизвестные, x3, x4 примем за
свободные, полагая x3=C1, x4=C2.
Тогда СЛАУ может быть записана в виде
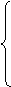 x1+7x2=6-3C1-2C2 x1+7x2=6-3C1-2C2
9x2=8-4C1-C2
x3=C1
x4=C2
Откуда находим
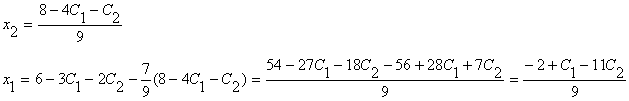
или окончательно получим

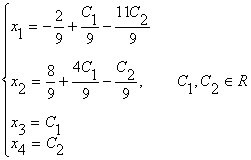
Пример 1.1.12. Решить систему
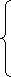 x1+2x2-3x3+x4=-4 x1+2x2-3x3+x4=-4
2x1-x2+x3-x4=2
-x1+3x2-x3+3x4=0
2x1+4x2-3x3 +2x4=3
Система линейных алгебраических уравнений несовместна.
Замечание. Однородные СЛАУ всегда совместны, т.к. ранги расширенной
матрицы системы и матрицы системы совпадают.
Вопросы для самопроверки
1. Какие матрицы называются равными?
2. В каких случаях возможно перемножение двух матриц ?
3. В каких случаях существуют произведения как АВ так и ВА?
4. Что называется минором и алгебраическим дополнением элементов
матрицы ? В чем отличие между ними ?
5. Сформулируйте правило Крамера.
6. Как осуществляется транспонирование матрицы ?
7. В чем суть метода элементарных преобразований получения обратной матрицы ?
8. Что такое ранг матрицы ?
9. Что такое основная и расширенная матрицы системы ?
10. Сформулируйте и поясните на примерах теорему Кронекера-Капелли.
Тема 1.2. Векторная алгебра
Учебники: [1, гл.1, § 1-3], [10, гл.2]/ [16, гл.7].
Аудиторная работа: [2, N1.4, 1.10(1), 2.1(1), 2.2(1), 2.3(1)-2.8(1), 2.28,
3.1(1), 3.8, 3.19(1), 3.20(1), 3.23], [7, гл.3, N1(1), 2, 3, 8(1), 10, 11(1),
12(1), 14(1)], [20, ч.1, гл.2, N2.9, 2.35, .2.43, 2.78, 2.79, 2.100(a),
2.102, 2.106(a), 2.107, 2.118, 2.127(a), 2.132, 2.137], [25, занятия
2(2.2.9,2.2.10), 3(3.2.1, 3.2.3, 3.2.5-3.2.7), 4(4.2.4-4.2.6), 5(5.2.2,
5.2.5-5.2.7)].
Самостоятельная работа: [2, N1.5, 1.7, 1.10(2,3), 2.1(2-5), 2.2(2), 2.3(2,
3)-2.8 (2,3) , 2.29, 2.30, 3.1(2,3), 3.19(2,3), 3.20(2)], [7, гл.3,
N1(2), 4, 6, 7, 8(2), 9, 11(2), 12(2), 14(2)], [20, ч.1, гл.2, N2.11,
2.32, 2.44-2.46, 2.82-2.84, 2.86, 2.100(б, в), 2.106(6,в), 2.108,
2.119, 2.127(6), 2.133, 2.134], [25, задания 2(2.3.6, 2.3.7), 3, 4, 5].
Для отвлеченного изображения конкретных векторных величин используются
векторы. Вектором (геометрическим) называется направленный отрезок прямой.
Два вектора называются равными, если они сонаправлены и имеют одинаковую
длину. Положение начальной точки таких векторов не играет никакой роли.
Поэтому геометрические векторы называются свободными.
При изучении темы «Векторная алгебра» студенту следует обратить внимание на
ниже рассмотренные вопросы.
1. Линейные операции над векторами (сложение, вычитание, умножение на число).
Векторы необходимо уметь складывать как по правилу треугольника, так и по
правилу параллелограмма.
2. Линейная комбинация векторов. Линейная зависимость и независимость
векторов. Базисные векторы. Декартов базис.
Пример 1.2.1. Указать при каких значениях α и β возможно равенство
αa + βb = 0, где а° и b° единичные векторы
(a0=a / |a|, b0=b / |b| ). Для решения приведенной задачи необходимо
рассмотреть возможное расположение векторов а и b :
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
| 


