|
Пример 1. 2.7. Вычислить площадь треугольника, построенного на векторах
а=2т+п и b = т- п , если |т|=2, |n|=1, (m,n)=
π/6
Вычислим векторное произведение векторов a, и b и воспользуемся формулой (1.2.9)
a´b =(2т+ п)-(т- n)= 2m´т- 2m´n+n´m-п´п =0-3m´n-0=-3m´n
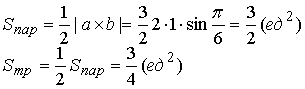
В декартовом базисе { i,j,k} векторное произведение векторов а(аx,аy,аz ) и
b(bx, by ,bz) вычисляется по формуле

Пример1.2.8. Найти координаты вектора b=(bx,by,bz
), если он перпендикулярен векторам a1 (2,-3,1) и a
2 (1,-2,3) и удовлетворяет условию;
b(i +2j-7k) = 10.
Вектор b перпендикулярен векторам a1 и a2. Поэтому его можнo искать в виде:
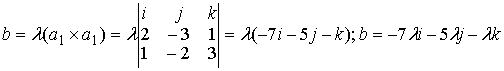
Удовлетворим условию b(i + 2j-7k)=10; -7λ -10λ +
7λ =10; -10λ=10, λ=-1.
Таким образом вектор имеет вид: b= 7i+5j+k.
Пример 1.2.9.Вычислить площадь треугольника, вершины которого расположены в
точках A(1,2,3), B(2,1,-1), С(3,-1,1).
SΔABC =1/2 |ABxAC|.Вычислим координаты векторов АВ и АС и
векторное произведение АВ´АС .
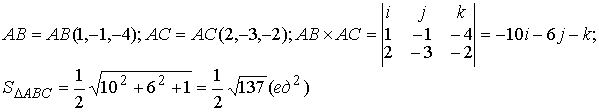
5.Смешанное произведение трех векторов.
Смешанным произведением трех векторов а,b,с называется число, которое
обозначается символом ахb-с (смешанное произведение иногда
называют векторно-скалярным).
Если векторы а,b,с некомпланарны, то смешанное произведение а
´b-с равно объему параллелепипеда, построенного на векторах
а,b,с, взятому со знаком "+", если упорядоченная тройка векторов а,b,с
-правая, и со знаком "-", если эта тройка - левая.
Из свойств смешанного произведения трех векторов следует отметить следующие:
1)при круговой перестановке векторов смешанное произведение не меняется, т.е. (
aх b)× с = (сха)× b = (bхс)× а;
2)если в смешанном произведении поменять местами два соседних сомножителя, то
произведение изменит знак, т.е. (aх b)× с = -(ах
с)× b ;
3) смешанное произведение равно нулю тогда и только тогда, когда векторы
компланарны, т.е. условием компланарности векторов является равенство нулю
смешанного произведения этих векторов.
Смешанное произведение векторов в декартовом базисе
{i,j,k}.Если а(ax, ay, az), b(bx, by, bz,) и с(сx, cy, cz), то

Условие компланарности векторов 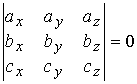 (1.2.12) (1.2.12)
Наиболее распространенные задачи, решаемые при помощи смешанного произведения:
1)найти объем параллелепипеда, построенного на векторах а,b,с:
V = |а х b× с|,
2) найти объем тетраэдра, построенного на векторах а,b,с:
V=1/6 (|а х b× с|)
3) проверить компланарны ли векторы а,b,с, если а х b×
с=0, то векторы компланарны, если а х b× с¹ 0,
то векторы некомпланарны;
4)проверить правую или левую тройку образуют векторы а,b,с,
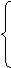 >0 -тройка векторов - правая , >0 -тройка векторов - правая ,
а х b× с=.
<0 - тройка векторов левая.
Замечание: смешанное произведение векторов а,b,с, как правило,
записывают в виде а× b× с .
Пример1.2.10. Вычислить длину высоты тетраэдра ABCD, проведенную из
вершины D к основанию АВС, если вершины тетраэдра имеют
координаты:
А (1,2,0), B(2,1,1), С(0,-3,-1), D(3,3,4). Найдем координаты векторов,
выходящих из вершины А:
АВ(1,-1,1), AC(-1,-5,-1), AD(2,1,4), Vтетр=1/6(|АВ×АС×AD|); Vтетр =1/3(SDABC×HD);
SDABC=1/2 (|AB´AC|); HD=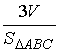 . Отсюда . Отсюда
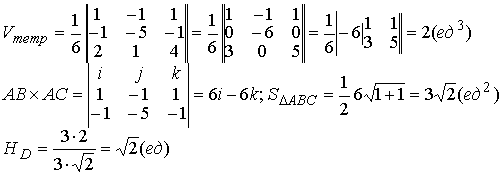
Вопросы для самопроверки
1.Сформулируйте правила треугольника и параллелограма сложения векторов.
2.Укажите принципиальное различие в формулах для вычисления длины
вектора в произвольном и декартовом базисах.
З. Чему равно скалярное произведение базисных векторов в декартовом
базисе?
4.Чему равно векторное произведение базисных векторов в декартовом
базисе?
5.Запишите условие компланарности векторов. Приведите пример.
6.Можно ли построить треугольник на векторах а,b,а+b ?
7.Приведите пример условия, при выполнении которого из трех векторов a, b,с
можно образовать треугольник.
8. Докажите, что объем тетраэдра вычисляется по формуле V=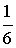 | а× b× с| | а× b× с|
9. Вычислите угол между векторами, совпадающими со скрещивающимися ребрами
тетраэдра.
10.Как Вы считаете, произведение векторов axbxc
(двойное векторное) является векторной величиной или скалярной?
Тема 1.3. Прямая и плоскость
Учебники:[1, гл.2, §1-3; 10, гл.4/ гл.5, §2-5; 16, гл.2, §1, 2, гл.10, §1,
2 (п.5), §3(п.7)].
Аудиторная работа: [2, 6.17(1-4), 6.18, 6.19(1), 6.20(3 6.21(1), 6.23(1),
6.25(1), 6.29, 6.34, 6.44(1)-6.47 (1), 6.50(1 6.51(1), 6.60(1) ,-6.62 (1)
,6.70(1) , 6.72J, [7, гл.З,Н15, 18(1— 19(1-4), 23(1),24(1), 26, 28(1),
30(1), 38, 41(1), 47(1) [20,ч.1, гл.2, N2.180(a)-2.184(a) , 2.185, 2.186,
2.189, 2.197(a 2.198, 2.199(a), 2.203(a)], [25, занятия 7(7.2.1-7.2.9),
8(8.2. 8.2.12), 6(6.2.1-6.2.2)] .
Самостоятельная работа: [2, 6.19(2,3), 6.20(2-5 6.21(2,3),
6.23(2,3), 6.24, 6.25(2-5), 6.26, 6.30, 6.44(2 6.47(2), 6.50(2-4),
6.51(2,3), 6. 60 (2, 3)-6. 62 (2, 3) , 6.70(2,3 6.73], [7, гл.З,М16, 18(4-
13), 19(5-11), 20, 21, 23(2,3), 24(2,3 30(2), 41(2), 47(2,4), 48], [20, ч.1,
гл.2, N2.180 (б)-2.184 (б 2.187- 2.188, 2.197(6), 2.200, 2.201, 2.203(6),
2.124], [2 занятия 7, 8, 6(6.2.1-6.2.4)].
При изучении аналитической геометрии в пространстве возникают
затруднения, связанные с недостаточностью пространственных
представлений. В таких случаях полезно пользоваться
пространственными моделями (тетрадь-плоскость; карандаш, ручка-прямая,
отрезок прямой) и использовать их при разборе теоретического материала
наравне с рисунками, приведенных в задачниках.
Различные виды уравнения плоскости
1.Уравнение плоскости, проходящей через данную точку М0(x0
,у0,z0) перпендикулярно вектору n(А,В,С) :
A(x-x0)+B(y-y0)+C(z-z0)=0
(1.3.1)
Пример 1.3.1. Записать уравнение плоскости, проходящей через точку M0
(1, 2, 3), перпендикулярно вектору n(2,-1,4). Используя уравнение (1.3.1),
получим 2(x-l)-l(y-2)+4(z-3)=0 или 2x-y+4z-l2-0.
Пример 1. 3 . 2.Составить уравнение плоскости, проходящей через точку М0
(1,2,3) пареллельно векторам a(3,-1.,0) и b(2,l,2).
Плоскость пареллельна векторам а и b, поэтому вектор нормали к
плоскости n(А,В,С) равен векторному произведению векторов)
а и b и находится по формуле (1.2.10):
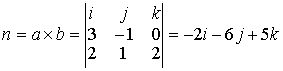
Уравнение искомой плоскости (1.3.1) имеет вид
-2(x-l)-6(y-2)+5(z-3)=0 или -2x-6y+5z-l=0 .
2.Общее уравнение плоскости:
Ax+By+Cz+D=0
(1.3.2)
В этом уравнении коэффициенты А, В,С -координаты вектора п(А,В,С)
перпендикулярного плоскости.
3.Уравнение плоскости в отрезках
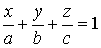
Числа a,b,c равны величинам направленных отрезков, отсекаемых на осях координат.
4.Уравнение плоскости, проходящей через три точки M1(x1
,y1,z1), M2(x2,y2,z2
) , М3(x3, у3, z3), не
лежащие на одной прямой
Пример 1.3.3.Составить уравнение плоскости, проходящей через три точки M
1(1,2,3), M2(-1,1,1) , М3(0,2,1) .
В соответствии с уравнением (1.3.4) получаем
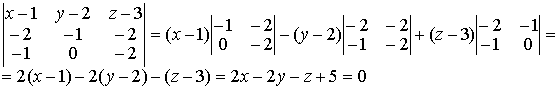
т.е. 2x-2y-z+5=0
и есть уравнение искомой плоскости.
Различные видах уравнений прямой в пространстве
 1.Общее уравнение прямой A1x+B1y+C1z+D1=0 1.Общее уравнение прямой A1x+B1y+C1z+D1=0
A2x+B2y+C2z+D2=0 (1.3.5)
Прямая задана пересечением двух плоскостей с нормалями n1(A1, B1, C1) и
n2 (A2, B2, C2)
2.Канонические (стандартные) уравнения прямой, проходящей через точку
М0 (x0, y0, z0) и имеющей направляющий вектор а(т,п,р)
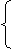
Пример 1.3.4.Перейти от общих уравнений прямой
2x+3y-z+2=0
x-y-3z+6=0 к каноническим уравнениям. Прежде всего выберем какую-
нибудь точку М0 , например М0 (0,0,2), удовлетворяющую
общим уравнениям прямой. Если сразу не удается подобрать координаты точки М
0 , то эту точку можно найти из решения системы линейных уравнений (см.
пример 1.1.11), которой задаются общие уравнения прямой.
Направляющий вектор прямой а может быть выбран в виде a=n1
xn2 (см. 1.3.5), где n1(2,3,-l) и n
2(1,-1,-3) -нормальные векторы к плоскостям, пересечением которых
и задается прямая
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
| 


