} называется n - мерным вектором, а числа х1, i=1,n,

составляющие эту совокупность на­зываются координатами вектора х;

n - мерный вектор можно рассматривать как матрицу-строку или матри­цу

столбец, состоящую из n элементов.

Линейным векторным пространством называется множество векто­ров (любой природы),

для которых определено два действия-сложение и умножение на произвольное число.

Линейные n-мерные векторные пространства будем обозначать Ln.

Если х={х1,х2,...хn} є Ln и у={у1, у2,... уп}є L, то

1. х = у , если хі = уі , i = 1, n

2. х+у = {х1 + y1,х2 + у2,. ...хп +уп „ } є Ln.

3. mх = {mx1, тх2,..., mxп} є Ln.

Приведенные определения позволяют рассматривать векторы обще­го вида не

обязательно геометрической природы.

Примеры линейных пространств:

а) множество геометрических векторов R3;

б) множество всех многочленов Рп(х), степени не превосходящей n;

в) множество матриц Amn, размерности mn;

г) пусть хi, i = 1,n -количество i-го сырьевого продукта,

измеренного в подходящих единицах, тогда векторы вида х={х1,х

2,...хn}могут задавать суточную потребность предприятия в

сырье, запасы сырья, хранящего­ся на складе и т.д.

Любая совокупность n линейно независимых векторов в n-мерном пространстве

образует базис в этом пространстве (определение линей­ной зависимости и

независимости векторов см. в теме 1.2).

Пример 1.5.1.Показать, что система векторов

образует базис в пространстве квадратных матриц

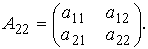
Представить матрицу А22 в виде линейной комбинации векторов Si, i=l,4.

Составим линейную комбинацию

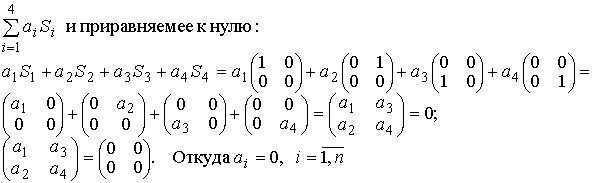
Mы получили, что линейная комбинация векторов Si , i=1,n

равна нулю лишь в том случае, когда все коэффициенты этой линейной комбинации

равны нулю. Согласно определения (см. тему 1.2) векторы Si ,

i=1,n линейно независимы и могут быть использованы в качестве базисных

векторов.

Разложение матрицы А22 по базису Si , i=1,n имеет вид:

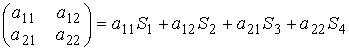
Линейное пространство называется евклидовьм, если в нем каж­дой паре

векторов х, y сопоставлено число, которое называется ска­лярным

произведением этих векторов, обозначается (х, у ) и удовле­творяет

аксиомам:

1.(х,у)=(у,х)

2. ( х1+ х2 , у ) = ( х1, у ) + (х2 , у)

3. (αх , у ) = α (х , у ) ;

4. (х, х )>0, х ≠ 0 и (x,x)=0, если х=0.

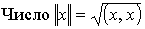
называется нормой вектора в евклидовом про­странстве.

Неравенство |(х,y)|≤║x

║х║y║называется неравенством Коши-Буняковского.

Два вектора евклидового пространства называются ортогональны ми, если их

скалярное произведение равно нулю, т.е. (х, у )=0.

Линейные преобразования. Если указано правило f, по

которому каждому вектору х линейного пространства Ln

ставится в соответствие единственный вектор у этого пространства,

то говорят, что в нем задано преобразование (отображение, оператор).

Преобразование f линейного пространства L называется

линейным (линейным оператором), если для любых векторов этого пространств х

1, х2 , х и любого λєR выполняются условия

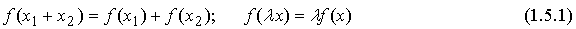
Если линейное пространство L n-мерное пространство, а f

линейное преобразование (оператор) осуществляющее отображениe y=f(x), x(x

n) є L, тo можно построить матрицу этого преобразования

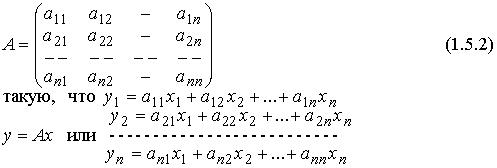
Замечание. Если вектор геометрический, то над ним ставится стрелка.

Пример 1.5.2. Показать, что преобразование y=a x x,

где а(а1,а2, а3) -постоянный

вектор, х(х1, x2, x3), y(y1,

y2, y3 ecть линейное в ли­нейном пространстве L3

и построить его матрицу А .

Чтобы доказать линейность преобразования y=a x x достаточно

проверить свойства (1.5.1).

Пусть x1, x2 є L3 , λєR ,

тогда у(х1+ х2) =а х (х1+ х

2) = а х х1 + а х х2

у(λх)= а х (λх)= λ (а х х), т.е. свойства

линейности (1.5.1) выполнены и преобразование y=a x x линейно.

Построим матрицу преобразования

Предположим в линейном пространстве Ln заданы базисы еi,

i=1,n и mi, i=1, а также матрица A линейного преобразования f

в базисе еi, i=1. Тогда матрица линейного преобразования в

базисе mi, i=1, будет иметь вид

B=T-1 AT,

(1.5.3)

где T -матрица перехода от старого базиса к новому.

Пример 1.5.3. В базисе e1 ,e2 преобразование f имеет матрицу

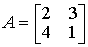
Найти матрицу преобразования f в базисе m1=е1 - е2 , т2=2ё2+3е2.

Матрица

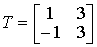
(координаты векторов m1 и т2

записываются в столбцы, соответственно в первый и второй).

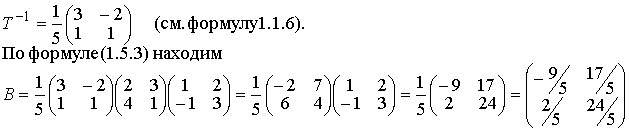
Собственные числа и собственные векторы матрицы линейного преобразования

(оператора)

Всякий ненулевой вектор х(а1,а2,...,аn

называется собственным вектором линейного преобразования, если

Ах=λx,

(1.5.4) где λ -некоторое число, называемое собственным значением

(числом) линейного преобразования.

Если матрица А имеет вид (1.5.2), то равенство (1.5.4) запи­сывается в

виде системы линейных алгебраических уравнений (Дц - Л)а^ -ь

a^a^+...+а^а^ = О

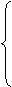(a11- λ)a1+a12a2+...+a1nan=0

a21a1+(a22- λ)a2+...+a2nan=0

-----------------------------------

(1.5.5)

an1a1+an2a2+...+(ann- λ)an=0

Система (1.5.5), однородная СЛАУ, имеет отличные от нуля (нетривиальные)

решения только тогда, когда определитель равен нулю. Отсюда следует, что

det(A- λE)=0.

(1.5.6)

Уравнение (1.5.6) называется характеристическим уравнением матрицы данного

линейного преобразования. Каждый действительный корень λ уравнения

(1.5.6) является собственным числом. Соответствующие собственному числу

координаты собственного вектора находятся из системы (1.5.5) методом,

изложенном в теме 1.1 (см. пример 1.1.11).

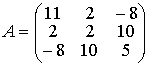
Пример 1.5.4.Найти собственные числа и собственные векторы матрицы линейного

преобразования

Система однородных линейных алгебраических уравнений (1.5.5) для

нахождения собственных векторов имеет вид

(11-λ)а1+2а2-8а3=0

2а1+(2-λ)а2+10а3=0

(1.5.7)

-8а1+10а2+(5-λ)а3=0

Вычислим определитель (1.5.6) и решим соответствующее характеристическое

уравнение

Характеристическое уравнение имеет вид

λ3-18 λ2-81 λ+1458=0, а его решение λ

1=9, λ2=18, λ3=-9. Найденные

зна­чения λі, і=1,3 подставим в (1.5.7)

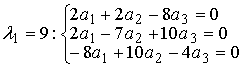
Решение этой системы х1= С(2,2,1)Т, С єR, а

соответствующий еди­ничный вектор х01 =(2/3, 2/3,

1/3) Т

При λ 2=18: х02=(-2/3, 1/3, 2/3)Т при λ3=-9 х03 =(1/3, -2/3, 2/3)

Решения систем линейных уравнений рассмотрены в теме 1.1 (см. пример 1.1.11).

Необходимо отметить следующие свойства собственных значений и собственных

векторов симметрической матрицы.

1.Корни характеристического уравнения вещественной симметрической матрицы

вещественны.

2.Собственные векторы вещественной симметрической матрицы, отве­чающие

различным собственным значениям ортогональны. (Проверьте на собственных

векторах матрицы примера 1.5.4).

Вопросы для самопроверки

1.Приведите примеры n-мерных векторов.

2.Что такое линейное векторное пространство, какое пространство

называется евклидовым?

З. Что такое базис в n -мерном пространстве?

4 . Как определяется линейное преобразование?

5.Докажите неравенство Коши-Буняковского.

6. Докажите неравенство ||x+y||≤||x||+||y||

7. При каком условии матрица линейного преобразования имеет диаго­нальный вид?

8.Сформулируйте алгоритм нахождения собственных векторов.

Тема 1. 6 . Квадратичные формы. Приведение к кано­ническому виду уравнений

линии и поверхности второго по­рядка

Учебники:[1, гл.3, §4],[10, гл.7, §2], [16, гл.11, §3].

Аудиторная работа:[2, N9.4(1, 3), 11.22(1)], [7,гл.3, §5, 6, N63(1,2)],

[20, ч.1, гл.4, §3, N4.226, 4.227, 4.233],[25, за­нятия 16(16.2.6(а,б)) ,

17(17.2.1, 17.2.2) ].

Самостоятельная работа: [2, N9.4(4-6), 11.22(2)], [7, гл.3, §5, 6,

N63(3-5)], [20, ч.1, гл.4, §3, N4.228, 4.289, 4.234],[25, задания

16(16.3.3(а,б, в) ) , 17(17.3.2, 17.3.3, 17.3.4(а,б,в)) ].

Квадратичной формой от трех переменных x,y,z называется одно­родный

многочлен второй степени относительно этих переменных.

F(x,y,z)= a11x2 + 2a12xу+ а22у

2 + 2a13xz+ 2a23yz+a22 z2

(1.6.1)

Если учесть, что а12 =a21, a13=a31, a23=a32 , то F(x,y,z) записывается

в виде

F(x, у, z) = а11х2 + а12ху + а