Определение. Функция f(x) называется непрерывной в точке а, если ее

предел в этой точке совпадает со значением функции в той же точке, или lim f(x)

= f(a).

Все элементарные функции непрерывны в каждой точке, где они определены.

Основные теоремы о пределах функций.

1. Предел суммы двух функций равен сумме пределов.

х→а

х→а

х→а

lim (f(x) + φ(x)) = lim f(x) + lim φ(x)

2. Предел произведения двух функций равен произведению пределов.

х→а

х→а

х→а

lim [f(x) * φ(x)] = lim f(x) * lim φ(x)

3. Предел произведения числа на функцию равен произведению числа на предел

функции.

х→а

х→а

lim С*f(x) = С *lim f(x)

Это свойство можно записать так: постоянный множитель выносится за знак предела.

4. Предел отношения двух функций равен отношению пределов этих функций.

(Кроме случая, когда знаменатель стремиться к нулю).

х→а

х→а

х→а

х→а

lim f(x) / φ(x) = lim f(x) / lim φ(x), limφ(х)≠0.

Если знаменатель стремиться к нулю, а числитель - нет, то говорят, что

отношение стремиться к бесконечности.

Бесконечность – это не число, ее можно добавить ко множеству вещественных

чисел R в качестве нового элемента ∞. После этого числовая прямая

превращается в так называемую расширенную прямую.

Раз мы добавили новый элемент ко множеству вещественных чисел, то запишем

арифметические операции с этим элементом ∞.

Пусть а любое вещественное число, а Є R, тогда

а + ∞ = ∞	-∞ + а = -∞	∞ * (-а) = - ∞, а › 0
∞ - а = ∞	-∞ - а = - ∞	∞ * ∞ = ∞
а * ∞ = ∞, а ≠ 0	∞ + ∞ = ∞	а/∞ = 0, ∞/а = ∞
	- ∞ - ∞ = - ∞

Есть особые случаи, когда предел суммы, произведения или частного нельзя

найти, зная только пределы слагаемых, сомножителей или делимого и делителя.

Такие случаи называются неопределенностями.

Выделяют неопределенности двух типов:

Арифметические неопределенности (0/0); (00/00); (00 – 00); (0 * 00).

Степенно-показательные неопределенности (100); (000); 00.

Эти записи не являются операциями над числами и 00, они представляют собой

только деловые обозначения.

В случае неопределенности предел может быть равен нулю, конечному числу,

бесконечности или не существовать. Для нахождения предела (раскрытие

неопределенности) надо исследовать каждый случай отдельно.

х→ -2

Пример 1. Найти lim [(х2 – 4) / (x2+x – 2)].

Решение:

х→ -2

1) Подставим точку х = - 2 в нашу функцию, получим lim [(х2 – 4) / (x2+x – 2)] =

= (4 – 4) / (4 – 2 – 2) = (0/0).

х→ -2

х→ -2

2) Раскроем эту неопределенность, разложив числитель и знаменатель на простые

множители, найдя корни числителя и знаменателя, тогда lim [(х2 – 4)

/ (x2+x – 2)] lim [(х – 2) * (x+2)] / [(x-1)*(x + 2)] = (-2 –

2)/(-2-1) = -4/ -3= 4/3/

х→ 00

Пример 2. lim [(х2 – 4) / (x2+x – 2)]

Решение:

х→ 00

х→ 00

х→ 00

lim [(х2 – 4) / (x2+x – 2)] = (00/00). Чтобы раскрыть

эту неопределенность, вынесем за скобки из числителя и из знаменателя х в

старшей степени, т.е. х2, получим: lim [(х2 – 4) / (x

2+x – 2)] = lim [(х2 *

х→ 00

х→ 00

(1 – 4/х2) / (x2(1+1/x – 2/x2)] = 1/1=1, т.к.

lim 4/х2 = 4 / 00 = 0, . lim 1/х =

х→ 00

1/00=0 и . lim 2/х2 = 2/00

Для раскрытия неопределенностей используются не только различные приемы

преобразования функций, как мы видели в примерах 1 и 2, но и так называемые

замечательные пределы.

х→ 0

Первый замечательный предел .lim sinx/х = 1, он раскрывает

неопределенность (0/0).

х→ 00

Второй замечательный предел. . lim (1+1/х)х = ℮, где ℮=2, 7, .

иррациональное «непперово» число. Это число часто берут за основание логарифма,

тогда такой логарифм обозначается так: log℮x = lnx и

называется натуральным логарифмом.

х→ 0

Пример. 3 Найти lim (sin3x)/х = (0/0).

х→ 0

х→ 0

Решение: lim (3sin3x) / (3х) = 3 lim (sin3x) / (3х) = 3*1 = 3

х→ 0

Пример. 4 Найти lim (sin5x)/(sin2х) = (0/0).

х→ 0

х→ 0

Решение: lim (sin5x / sin2х) = lim [((sin5x / 5х)*5x) / ((sin2x / 2x) * 2x)]

х→ 0

х→ 0

= 5/2 * [(lim (sin5x / 5х)) / lim (sin2x / 2х)] = 5/2

х→ 00

Пример. 5 Найти lim (1+(1/2x))x = 100.

х→ 0

Решение: lim (1+(1/2x))2x * (1/2) = ℮1/2=℮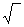

х→ 00

Пример. 6 Найти lim (1+(1/(x-1))x = 100.

х→ 00

х→ 00

Решение: lim [1+(1/(x-1))]x -1+1 = lim [(1+(1/(x-1)))x -1

* (1+(1/(x-1)))1] = ℮*1 = ℮

Тема 11. Производная и дифференциал.

Приращение аргумента, приращение функции.

0

Пусть функция у= f(х) определена в точке х0 и некоторой ее

окрестности, придадим точке х0 приращение Δх и получим точку х

0+Δх, значение функции в этой точке – f(х0+Δх).

Разность значений f (х0+Δх) – f(х0) называется

приращением функции, обозначается приращение функции Δf или Δу, т.е.

Δf=f(х0+Δх) – f(х0). Рис. 1

у Рис.1

			У = f(х)

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13