|
событий.
Размещения. Перестановки, сочетания.
Всевозможные группировки из данных n элементов по м в каждой, отличающиеся друг
от друга либо самими элементами. Либо порядком расположения эл-в, называют
размещениями из к элементов по m.
Например, размещения из 3-х эл-в а,б,с: аб,ас,ба,бс,са.сб. Число всех размещений
из n эл-в вычисляют: Anm=n!/(n-m)!
Перестановками из n эл-в наз их группировки, отличающиеся друг от
друга только порядком входящих в них эл-в. Например, перестановки из а,в,с:
авс,сва,вас,вса, асв,сав. Число всех различных перестановок: Рn= n!
Всевозможные группировки из данных n эл-в по m в каждой, отличающиеся друг от
друга хотя бы одним элементом, наз сочетаниями из n эл-в по m.
Пример: сочетания из а,в,с,д по 2:ав, ас, ад, вс, вд, сд.
Число всех сочетаний из n эл-в по m:
Cnm = n!/(m!*(n-m)!).
5. Классический способ подсчета вероятностей.
Опыт (Е) ® множество элементарных исходов: А1, А2.:
1) все Аi равновозможные
2) любые два исхода несовместны
3) А1 È А2 È. = W
Р {А} = m/n, где n – общее число элементарных исходов, связанных с Е, m –
число элементарных исходов, приводящих к А
6. Геометрические вероятности
Геометрические вероятности – вероятность попадения точки в область (отрезок,
часть плоскости и т. д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу ставится
точка (поставленная точка может оказаться в любой точке отрезка L),
вероятность попадения точки на отрезок l пропорциональна длине этого отрезка
и не зависит от его расположения относительно отрезка L. Вероятность
попадения точки на отрезок l определяется равенством
P =Длина l / Длина L.
Пусть плоскость фигуры g составляет часть плоскости фигуры G. На фигуру G
наудачу брошена точка, т. е. брошенная точка может оказаться в любой точке
фигуры G. Вероятность попадения брошенной точки на фигуру g пропорциональна
площади этой фигуры и не зависит ни от ее расположения относительно G, ни от
формы g. Вероятность попадения точки в фигуру g определяется равенством P =
Площадь g / Площадь G.
7. Правило сложения вероятностей.
Если событие А и В несовместны, то Р{А + В} = Р{А} + Р{В}
Доказательство:
Е, Nраз , NА раз наблюдалось событие А, NВ раз
наблюдалось событие В, NА+В раз наблюдалось событие А+В.
Так как А и В несовместны, то NА+В = NА + NВ, NА+В / N = NА / N+ NВ / N.
Если устремить N ® ¥, то получается Р{А + В} = Р{А} + Р{В}
Обобщение: Если А1, А2, . , Аn – попарно несовместны, то
Р{А1 + А2 + . + Аn } = Р{А1} + Р {А2}+ . + Р {Аn}
8. Условная вероятность. Правило умножения вероятностей
Пусть A и В – два случайных события по отношению к некоторому опыту s, причём
р(В) не равно нулю. Число р(АВ)/р(В) называется вероятностью события А
при условии, что наступило событие В, или просто условной вероятностью
события А. Таким образом рв(А) = р(АВ)/р(В). Пусть N – общее число
экспериментов, NB - число экспериментов, в которых имело место
событие В. NАВ – Число экспериментов, в которых имели место события
А и В одновременно. Отношение NАВ/NB – частота события А
при условии, что наступило событие В.
р(АВ)=рВ(А)р(В) – Вероятность произведения двух событий равна
вероятности одного из этих событий при условии другого, умноженной на
вероятность самого условия. Аналогичная формула справедлива для трёх событий.
р(А1А2А3)=р(А1)рА1(А
2)рА1А2(А3)
А не зависит от В, если выполняется равенство рВ(А)=р(А).
Наступление В не оказывает влияния на наступление события А.
Правило умножения вероятностей - Если событие А не зависит от В, то
справедливо равенство р(АВ)=р(А)р(В). (веростность произведения равна
произведению вероятностей)
9. Формула полной вероятности. Формула Байеса
Если события Н1, Н2,.,Нn попарно несовместны и
образуют полную группу, то для вероятности любого события А справедлива формула
р(А)=рН1(А1)р(Н1)+рН2(А)р(Н2
)+.+рHn(А)р(Нn). Вероятность события А равна сумме
произведений условных вероятностей этого события по каждой из гипотез на
вероятность самих гипотез.
Формула Байеса. (условие – событие А может наступить только с одной из
гипотез). Эта формула определяет вероятность, что имела место именно эта
гипотеза.
Вывод формулы.
p(AHi)=pHi(A)p(Hi)
p(HiA)=pA(Hi)p(A) приравниваем правые части, получим
pHi(A)p(Hi)=pA(Hi)p(A) воспользуемся формулой полной вероятности.
pA(Hi)= рHi(A)p(Hi) .
рН1(А1)р(Н1)+рН2(А)р(Н2)+.+рHn(А)р(Нn)
10. Дискретная СВ и ее закон распределения.
Величина, принимающая в результате испытания (опыта) определенное значение,
называется случайной величиной. СВ Х называется дискретной, если
существует конечное и счетное множество S={х1, х2,.}
такое, что Р(ХÎS)=1. Числа х1, х2,.называются
возможными значениями СВ Х.
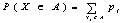 Пусть рi=Р(Х=хi Пусть рi=Р(Х=хi
) – вероятность возможного i-го значения. При хi ≠ хj
события Х=хi и Х= хj несовместны. Применяя правило
сложения вероятностей для несовместных событий получим:
Таблица
называется законом распределения дискретной СВ Х. Для любой СВ функция
распределения – F(x)=P(X<x) . В случае дискретной СВ функция распределения
имеет вид
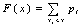
F(x) – ступенчатая функция со скачками в х1, х2,., причем величины скачков
равны р1, р2,.
11. Числовые хар-ки СДВ.
Математическим ожиданием дискретной СВ Х, множество
возможных значений которой конечно, называется сумма произведений всех ее
возможных значений на их вероятности: М(Х)=х1р1+х2
р2+.+хnpn
Свойства. 1.Матем. ожидание константы равно константе: М(С)=С
2.Постоянный множитель можно выносить за знак математического ожидания:
М(СХ)=СМ(Х)
3.Математическое ожидание суммы СВ равно сумме мат. ожиданий слагаемых:
М(Х1+Х2+.+Хn)=M(X1)+M(X2)+.+M(Xn)
4.Математическое ожидание произведений независимых СВ равно произведению
математических ожиданий сомножителей. (дискр.СВ наз. независимыми, если Р(Х
1=а1,.Хn=an)=P(X1=a1)*.Р(Xn=a
n).
Для любой СВ Х разность Х-М(Х) называется отклонением Х. Математическое ожидание
квадрата отклонения СВ Х называется дисперсией Х. По определению
D(X)=M(X-M(X))2.
Стандартное отклонение СВ Х определяется как корень квадратный из дисперсии и
обозначается s(х). Из свойств математического ожидания: D(X)=M(X2
)-M(X)2
Свойства. 1.Прибавление (вычитание) константы к СВ не меняет ее дисперсии
D(X+C)=D(X)
2.Постоянный множитель выносится из-под знака дисперсии в квадрате D(СX)=С2D(X)
3.Дисперсия суммы независимых СВ равна сумме дисперсий слагаемых
D(X1+.+Xn)=D(X1)+.+ D(Xn)
Важно помнить, что дисперсия константы равна 0: D(C)=0
Начальным моментом порядка К СВ Х называют математическое ожидание
величины Хк : nк=М(Хк)
Центральным моментом порядка к случайной величины Х называют математическое
ожидание величины (Х-М(Х)) к
mк=М[(X-M(X)) к]
Cоотношение, связывающее начальные и центральные моменты: m2=n2-n12
При изучении распределений, отличных от нормального, возникает необходимость
количественно оценить это различие. С этой целью вводят специальные
характеристики – асимметрию и эксцесс (для нормального распределения эти
характеристики равны 0). Асимметрией теоретического
распределения (теоретическим называют распределение вероятностей) называют
отношение центрального момента третьего порядка к кубу среднего квадратического
отклонения: Аs=m3\s3
Эксцессом теоретического распределения называют характеристику, которая
определяется следующим равенством: Ек=(m4\s4)-3
12 Биномиальное, Пуассоновское, геометрическое и гиппергеометрическое
Биномиальным распределением С параметрами n и р наз
распределение числа успехов в n независимых испытаниях с вероятностью успеха в
каждом испытании р. Биномиальное распред-е имеет вид:
| Х | 0 | 1 | 2 | . | n | | Р | Cn0p0qn | Cn1p1qn-1 | Cn2p2qn-2 | . | Cnnpnq0 |
Где q = 1-р. Для случайной величины Х, распределенной по биномиальному закону
с параметрами n и р, M(X)=np, D(X)=npq.
Пуассоновское распределение с параметром λ>0
задается следующей бесконечной таблицей
| Х | 0 | 1 | . | k | . | | Р | e-λ | λ e-λ /1! | . | λke-λ /k! | . |
M(x)=D(X)=λ
Геометрическим распределением с параметром р наз
распределение числа испытаний до первого успеха в серии независимых испытаний с
вероятностью успеха в каждом испытании. Оно имеет вид бесконечной таблицы:
Для дискретной случайной величины. Распределенной по геометрическому закону,
M(X)=1/p, D(X)=q/p2.
Гипергеометрическое распределение . Рассмотрим пример.
Пусть в партии из N изделий имеется М стандартных. Из нее случайно отбирают n
изделий, причем отобранное изделие не возвращается в партию. Пусть Х- С.В.-
число m изделий среди n отобранных. Найдем Р(Х=m):
(1) - Общее число элементарных исходов = СnN. (2) - Число
исходов, благоприятствующих событию Х=m,(среди взятых n изд-й ровно m
стандартных)= СmM Сn-mN-M
(m стандартных изделий можно извлечь из М СmM способами,
при этом остальные n-m изделий д.б. нестандартными, последние мы извлкаем из
N-M нестандартных изделий Сn-mN-M способами).
Искомая вероятность равна отношению (1) к (2):
Р(Х=m)= СmM Сn-mN-M / СnN
Причем, если n Значительно меньше N, то гипергеометрич. Распределение дает
вероятности, близкие к вероятностям, полученным по биномиальному закону.
13 Функция распределения случайной величины.
Определение. Функцией распределения случайной величины x называется
функция F(x) = P{x < x}
Свойства F(x):
1) Зная F(x), можно найти P{x1 £ x < x2}
{x < x2} = {x < x2} È {x1 £ x < x2} Þ P{x < x2} = P{x < x2} È P{x1 £ x < x2}Þ
Þ P{x1 £ x < x2} = F(x2) - F(x1)
2) Функция F(x) неубывающая, причем 0 £ F(x) £ 1
Если x2 > x1, то F(x2) ³ F(x1) ( P{x < x2} ³ P{x < x1} )
3) Справедливы равенства:
а) lim F(x) = lim P{x Î (-¥; x)} = 1; b) lim F(x) = 0
x ® +¥ x
® +¥
x ® - ¥
4) Функция F(x) = lim F(x - a) º F(x – 0)
a ® 0, a > 0
5) P{x = x} = F(x+0) – F(x-0); где F(x+0) º lim F (x + a)
a ® 0, a > 0
14. Непрерывные случайные величины
Случайная величина x называется непрерывной, если непрерывной является ее
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
| 


