Дано: f(x) и g(x) – непрерывны в x0 Û lim f(x) = f(x0); lim g(x) = g(x0)

X ® Xo X ® Xo

lim (f(x)•g(x)) = limf(x)•lim g(x) (по свойству предела функции) = f(x0

)•g(x0) (по

X ® Xo X ® Xo X ® Xo

определению непрерывности) ® F(x) = f(x)•g(x) непрерывна в x0.

2) f(x) – непрерывна

в точке x0, существует такая окрестность точки

f(x0) > 0 x0

, во всех точках которой f(x) > 0.

15. Основные элементарные функции:

1. Степенные функции: y = xa,

где а – любое постоянное число. Областью определения считается промежуток x >

0, но если, например, а–натуральное число, функция определена для всех х.

2. Показательная функция: y = ax,

где a > 0, a ≠1. Область определения – множество всех действительных чисел.

3. Логарифмическая функция: y = logax,

где a > 0, a ≠1. Область определения: x > 0.

4. Тригонометрические функции: y = sin x, y = cos x, y = tg x, y =

ctg x.

Область определения для sin x и cos x – множество действительных чисел.

5. Обратные тригонометрические функции: y = arcsin x, y = arccos x, y

= arctgx.

Область определения x Î [-1; 1] для arcsin x и arccos x, множество

действительных чисел для arctg x.

Действия над функциями, которые считаются допустимыми:

1. все арифметические действия (f + g, f – g, f•g, f/g);

2. построение сложной функции.

Элементарными функциями называются такие, которые получаются из основных

с помощью допустимых действий.

Элементарные функции непрерывны в каждой точке своей области определения.

16. Теорема о непрерывности сложной функции.

Пусть даны две функции x = φ(t) с областью определения Т и множеством

значений Х, и y = f(x) с областью определения Х и множеством значений Y.

Тогда «цепное правило: φ f

t ® x ® y

определяет новую функцию с областью определения Т. Эта новая функция

обозначается y = f ( φ(t) ) и называется сложной функцией.

Если x = φ(t) – непрерывна

в t0 Þ y = f ( φ(t) ) –

непрерывна в t0

y = f(x) – непрерывна в x0 = φ(t0)

Доказательство:

x = φ(t) – непрерывна в t0 Û Δt ® 0 Þ Δφ ® 0 (Δx ® 0)

y = f(x) – непрерывна в x0 Û Δx ® 0 Þ Δf ® 0

↓

Δt ® 0 Þ Δx ® 0 Þ Δf ® 0 (Δt ® 0 Þ

Δf ® 0)

y = f(φ(t)) – непрерывна в t0

17. Теорема о непрерывности обратной функции.

Пусть y = f(x) - функция с областью определения X (D(f) = X) и областью

значений Y (E(f) = Y). При этом разным значениям х отвечают разные значения y.

Тогда для каждого значения y Î Y существует только одно x Î Х,

такое , что f(x) = y. Если мы сопоставим каждому y Î Y именно такое x, то

получим отображение множества Y в множество X. Это отображение называется

обратным к данному отображению f и обозначается f -1 , т. е.

обратная функция для y = f(x) есть x = f –1(y).

Пусть y = f(x) (x Î D (f)) непрерывна и возрастает на отрезке [a; b],

тогда обратная функция x = f—1(y) также непрерывна и возрастает на

[f(a); f(b)].

(аналогично для непрерывной убывающей функции).

18. Односторонняя непрерывность. Точки разрыва, их 7классификация.

Функция , определённая в некоторой окрестности точки х0, называется

непрерывной в этой точке, если предел функции в точке х0 существует

и равен значению в этой точке.

Функция f(x), определённая на отрезке [a,b], называется непрерывной в точке а

справа, если lim f(x)=f(a) (аналогично слева)

x®a+0

Функция y=f(x) непрерывна на Х, если эта функция непрерывна в каждой точке

этого промежутка.

Если lim f(x) не равен lim f(x0)

X®Xo

,то х0 - точка разрыва непрерывности этой функции.

Классификация точек разрыва.

1. х0 – точка разрыва первого рода, если одосторонние пределы

существуют, но они не равны между собой.

1.1 Точка устранимого разрыва, если односторонние пределы равны между собой,

но их значение не совпадает со значением функции в этой точке.

Lim f(x)=lim f(x) не равен f(x0)

X®Xo-0 X®Xo+0

1.2 Точка разрыва с «конечным скачком». Правый и левый пределы не совпадают.

1.3 Точка разрыва с «бесконечным скачком». Хотя бы один односторонних

пределов бесконечен.

2. х0 - точка разрыва второго рода, если хотя бы один из

односторонних пределов не существует.

1. Производная функции и ее геометрический смысл.

Приращением функции y =f(x) в точке x0 называется разность

Δу=f(x)-f(x0)= f(x+Δx)-f(x0)

Производной от функции y=f(x) в точке х0 наз. Предел отношения

Δу/Δх, когда Δх→0 (при усл., что этот предел существует)

Написать обозначение производной.

Геометрический смысл производной.

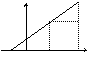
Пусть Г- график функции y=f(x). Рассмотрим на Г т. А(x0,f(x0)) и т. В

(x0+Δx,f(x0+Δx))

В

С

y=f(x) А

Прямая АВ называется секущей. Будем считать, что y=f(x)-непрерывная функция,

тогда если Δх→0, то f(x0+Δx)→f(x0), т.е. В→А при

Δх→0.

Пусть γ – угол наклона секущей относительно оси ОХ. Если существует

предел lim γ=γ0 при Δх→0, то прямая, проходящая через А

и образующая с осью ОХ угол γ0, называется касательной к Г в точке А.

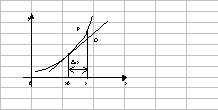
Пусть С(f(x0+Δх), f(x0)) – точка, дополняющая отрезок АВ до прямоуг.

треугольника АВС. Т.к. АС//ОХ, то tgγ =Δу/Δх. Переходя к

пределу, получим: tgγ0=f′(x0)

Т.е. геометрический смысл производной состоит в том, что f′(x0) – это

тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x0

)).

2. Уравнение касательной.

Найдем ур-е касательной к графику Г ф-и y=f(x) в точке А(х0, f(x0)): т.к. т.

А принадлежит Г и ур-ю касательной, то f(x0)=kx0+b, откуда b= f(x0)-kx0,

значит, касательная задается след. Ур-м:

y= kx+ f(x0)-kx0= f(x0)+k(х-x0)

Т.к. k= f′(x0), то

y=f(x0)+ f′(x0)(х-х0).

3. Односторонние производные.

Правой(левой) производной от y=f(x) в точке x0

называется предел f′(x0)=lim (f(x+Δx)-f(x0))/Δх при

Δх→0+0(Δх→0-0).

Если левая и правая производные функции в точке x0 сущ-т, и они

равны, то производная f′(x0) сущ-т и равна им. Если же левая и правая

производные функции в точке x0 не равны, то y=f(x) не имеет

производной в точке x0.

Правила дифференцирования

Теорема. Если функции u=f(x), v=g(x) дифференцируемы в

точке х0, то сумма, разность, произведение и частное этих функций также

дифференцируемы в точке ч0 и выполняются следующие формулы:

(U+(-)v)′=u’+(-)v’

(uv)’= u’v + uv’

(u/v)’= (u’v - uv’)/v2

4. Производная сложной и обратной функций.

Теорема. Если функция y=f(x) дифференцируема в точке t0, g(t0)=x0, то

сложная функция y=f(g(x)) также дифференцируема в точке t0 и выполняется след.

Формула:

f’(g(x))=f’(x0)*g’(t0)

Теорема. Если y=f(x) имеет обратную ф-ю x=g(y) и в точке х0 производная

f′(x) не равна 0, то обратная функция g(y) диф-ма в точке y0=f(x0) и

g’(y)=1/f(x0)

5. Производная элементарных функций.

Обл. определения производной f’(x) явл. множество всех точек x0

, в которых y=f(x) имеет конечную производную.

Производная каждой элементарной ф-и явл. элементарной ф-ей.

Производная логарифмической ф-и: (logax)’=1/xlna

Производная показательной ф-и: ax= ax lna

Производная степенной ф-и: (xa)’ = axa-1

Производная тригонометрической функции:

(Sinx)’=cosx

(tgx)’=1/cos2x

Производные обратных тригонометрических функций:

(Arcsinx)’=1/(1-x2)1/2

(arctgx)’=1/(1+ x2)

6. Понятие функции, дифференцируемой в точке.

Опр. Функция у=f(x) называется дифференцируемой в точке х0

, если ее приращение в х0 можно представить в виде

∆у=А∆х+α(∆х)∆х (*), где А – некоторое число,

α(∆х) – функция от ∆х, являющаяся бесконечно малой при

∆х→0. Связь между дифференцируемостью функции в точке и

существованием производной в этой же точке устанавливает Теорема.

Теорема. Для того чтобы f(x) была дифференцируема в точке х

0, необходимо и достаточно, чтобы она имела в этой точке конечную

производную.

Доказательство. 1.Необходимость. Пусть функция у=

f(x) дифференцируема в х0. Тогда ее приращение можно представить

в виде (*). Следовательно

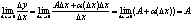
Следовательно производная существует и равна А. 2.Достаточность.

пусть существует конечная производная f ′ (х0

)=А. Тогда по определению производной, lim∆х→0

(∆у/∆х)=А. положим, что α(0)=0 и α(∆х)=

(∆у/∆х) – А, если ∆х≠0. Определеннная так функция

α(∆х) является бесконечно малой при ∆х→0. Действительно

lim∆х→0α (∆х)= lim∆х→0

((∆у/∆х) – А)=А – А=0. Кроме того ,

∆у=А∆х+α(∆х)∆х. Тем самым доказано, что функция

дифференцируема в х0.

Замечание. Если функция дифференцируема в х0, то из (*)

следует, что ∆у→0, когда ∆х→0, т.е. функция непрерывна

в данной точке. Обратное утверждение неверно. Функция может быть непрерывной,

но не дифференцируемой в данной точке.

Пусть f(x) дифференцируема в х0 ,следовательно, существует

производная и коэффициент А из (*) совпадает с производной, как следует из

доказательства теоремы. Тогда формулу (*) можно представить

f(x)=f(х0)+ f ′ (х0) ∆х

+α(∆х)∆х. α(∆х) б.м. функция

(∆х→0)

(**)

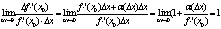
∆f(х0)~ f ′ (х0) ∆х

(приращение функции эквивалентно произведению производной на приращение

аргумента)

7. Дифференциал функции в точке

Опр. Диф-м функции в х0 наз. линейная относительно приращения

аргумента часть приращения функции в этой точке, эквивалентная всему

приращению.

d f(х0)= f ′ (х0) ∆х;

∆х=dх; df(х0)= f ′ (х

0) dх

Геометрический смысл. Уравнение касательной в х0 эквивалентно уравнению

у=f(х0)+ f ′ (х0) ∆х (***)

сравнивая (**) и (***) видим, что расстояние от точки Р(х, f(x)) на

графике до точки Q (x, f(х0)+ f ′ (х0

) ∆х) на касательной равно α(∆х)∆х, т.е. является

бесконечно малой более высокого порядка, чем ∆х, когда ∆х→0.

Вывод: геометрический смысл дифференцируемости f(x) в точке х

0 состоит в том, что расстояние от точки на ее графике до соответствующей

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12