|
на касательной стремится к нулю "быстрее", чем ∆х.
8. Приближенные вычисления.
Df(x0)»f '(x0) Dx
f(x0+Dx)- f(x0) » f '(x0) Dx Dx®0
f(x0+Dx) = f(x0)+ f '(x0) Dx
9. Эластичность функции и ее свойства.
Эластичностью функции y = f(x) в точке х0 называется следующий предел
Eyx(x0) = lim ((Δy/y): (Δx/x)).
Δx ® 0
Говорят также, что Еxy(x0) – это коэффициент эластичности y по x.
(При достаточно малых Δx выполняется приближенное равенство
(Δy/y): (Δx/x) » Еy Þ Δy/y » Еy Δx/x.
Эластичность Ey – это коэффициент пропорциональности между
относительными изменениями величин y и x.)
Еyx(x0) = lim ( [(f(x0 + Δx) – f(x0
))/f(x0)] : [Δx/x0] ) = (x0/f(x0
))f’(x0)
Δx®0
Ey = (x/y)y’.
Если y’/y представить как логарифмическую производную, то получается
Ey = x(lny)’
x = 1/(1/x) = 1/(lnx)’ Þ Ey = (lny)’/(lnx)’
Свойства эластичности (эластичность во всех последующих примерах
будет браться по x)
1) Eky = Ey
Eky = x (ln (ky))’ = x (ln k + ln y)’ = x(ln y)’ = Ey
2) Euv = Eu + Ev
Euv = x (ln uv)’ = x (ln u + ln v)’ = x(ln u)’ + x(ln v)’ = Eu + Ev
3) E u/v = E u – Ev
4) y = y1 + y2; y1, y2 > 0
Emin £ Ey £ Emax
Emin = min {E(y1), E(y2)}
Emax = max {E(y1), E(y2)}
(Лемма a/b, c/d – дроби; a/b £ c/d Þ a/b £ (a+c)/(b+d) £ c/d)
E(y) = y’x/y
E (y1 + y2) =( (y1 + y2)’/ (y1 + y2))•x = ( (y1’ + y2’)/ (y1 + y2))•x
E(y1) = (y1’/y1)x; E(y2) = (y2’/y2)x
Из леммы получаем: (y1’/y1)x £ ( (y1’ + y2’)/ (y1 + y2))•x £ (y2’/y2)x Þ
Þ Emin £ Ey £ Emax
5) Для функций y = f(x) и x = g(t) эластичность y по tв точке t0
удовлетворяет следующему равенству:
Eyx(t0) = Eyx(g(t0))Ext(t0).
Eyt(t0) = (ln y)’t = (ln y)’
t (ln x)’t = (ln y)’x xt’
Ext(t0) = Eyx(g(t0))Ext(t
0)
(ln t)’t (ln x)’t (ln t)’t (ln x)’x xt’
6) Для функции y = f(x) эластичность обратной функции x = g(y) в точке x
0 удовлетворяет соотношению:
Exy(y0) = E –1yx(g(y0)).
Поскольку g (y) – обратная функция, то выполняется тождество
f(g(y)) = y
По свойству 5) получается Eyx(g(y0))Exy(y0
) = Eyy(y0) = lim((Δy/y):(Δy/y)) = 1 Þ
Þ Eyx(g(y0))Exy(y0) = 1 Þ Exy(y0) = E –1yx(g(y0))
10 Производная сложной и обратной функции.
Теорема.Если функция y=f(x) имеет обратную функцию x=g(y) и в
точке х0 производная f¢(x) не равна нулю, то обратная функция
g(y) диффернцируема в точке у0=f(x0) и g¢(y0
)=1/f(x0) или x¢y=1/y¢x.
Доказательство.
Пусть а=f¢(x0). Тогда из дифференцируемости f(x) в х0
следует, что приращение Dу= f(x0+Dх) - f(x0) можно
представить в виде Dу=аDх+аDх=(а+а) Dх, где а=а(Dх)®0 при Dх®0. Так как а не
равно нулю, то отсюда следует, что Dх®0, когда Dу®0. Имеем
g¢(y0)= lim g(y+Dy)-g(y0) = lim Dx =lim ìDyü-1 = 1 .
Dy®0 Dy Dy®0 Dy Dy®0 îDxþ f¢(x0)
Теорема.Если функция у=f(x) дифференцируема в точке t0
и g(t0)=x0, то сложная функция y=f(g(x)) также
дифференцируема в t0 и выполняется следующая формула: d f(g(t))/dt|
t=to=f¢(x0)*g¢(t0) или y¢
t=y¢x*x¢t.
Доказательство.
Функция y=f(x) дифференцируема в точке х0, поэтому её приращение
можно представить как Dy=f¢(x0)+a(Dx)*Dx. Где Dx®0
при Dt®0 поскольку функция g(t) непрерывна (следствие дифференцируемости) в
точке t0. Так как а(Dx)®0 при Dx ®0 и при Dt®0. Поэтому
d f(g(t))|t=to=lim (f¢(x0)) Dx +a(Dx) Dx =
dt Dt®0 Dt Dt
=f¢(x0)g¢(t0)+0*g¢(t0)= f¢(x0)g¢(t0).
11. Производная основных элементарных функций.
Производная логарифмической функции. y=logax
Dy=loga(x+Dx)-logax=loga(1+Dx/x)=1 loga(1+Dx/x)= 1loga(1+t)=1 loga(1+t)1/t
Dx Dx Dx x Dx/x x
t x
где t=Dx/x Используя непрерывность функции logax в точке х=е и первый
замечательный предел, найдём производную логарифмической функции: (logа
х)¢= 1(logа(lim(1+t)1/t) = 1loga
e= 1.
x t®0 x x lna
Производная показательной функции.
У=ах является обратной для функции х=logау. По теореме
у¢х= 1= 1 =ylna
x¢y 1/ylna
Поскольку у=ах, получаем (ах)¢=ахlna.
Производная степенной функции.
Функция у=ха при х>0 может быть представлена в виде ха
=еalnx. Найдём (ха)¢=( еalnx)¢= е
alnx(alnx)¢=ха*а/х=аха-1 Аналогично
доказывается для x<0.
Производные тригонометрических функций.
С помощью формулы sinа-sinb=2sin[(a-b)/2]*cos[(a+b)/2] , первого
замечательного предела и непрерывности функции cos x найдём
(sinх)¢=lim sin (х+Dх) – sinх= lim 2sin(Dх/2) cos(х+Dх/2) =
Dx®0 Dx Dx®0 Dx
=lim sin(Dх/2) cos(х+Dх/2) = cos x
Dx®0 Dx/2
Для нахождения производных функций cos x и tg x можно использовать тождество
cos x=sin(x-p/2) , правило дифференцирования сложной функции.
Итак, (sin х)¢=cos x, (cos x)¢= - sin x, (tg x)¢=1/cos2 x.
Производные обратных тригонометрических функций.
Функция у=arcsinx является обратной для функции х=sinу. Следовательно,
(arcsinx)¢x= 1 = 1=
1= 1
(siny)¢y cosy Ö1-sin2xØ Ö1-x2Ø
Аналогично находятся остальные обратные тригонометрические функции.
(arcsinx)¢=1/Ö1-x2Ø, (arccosx)¢= -
1/Ö1-x2Ø, (arctgx)¢=-1/(x2
+1).
12. Правило Лопиталя
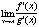 Теорема (правило Лопиталя Теорема (правило Лопиталя
). Пусть А – число, символ одностороннего предела (А=а±0) или символ
бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно
малые, либо обе бесконечно большие при х→А. Тогда, если существует предел
(конечный или бесконечный),
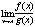
то существует и предел при этом выполняется равенство:
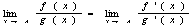
Доказательство:
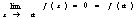 Доказательство теоремы дадим в Доказательство теоремы дадим в
случае, когда ƒ(х) и g(х) – бесконечно малые функции и А=а –
число. Изменим, если это необходимо, определение функций ƒ(х) и g(х) в
точке а так, чтобы значения этих функций в точке а были бы равны нулю:
ƒ(х) = g(х)=0. Так как
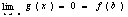 и и
то ƒ(х) и g(х) непрерывны в точке а, и к этим функциям можно
применить теорему Коши. Учитывая, что ƒ(а) = ƒ(b)=0, получим

для некоторой точки с, расположенной между точками а и х
. При х→а имеем с→а и, следовательно если ƒ(х)→0 и
g(х)→0 (соответственно, |ƒ(х)|→+∞,
|g(х)|→+∞), когда а→А. Правило Лопиталя позволяет во
многих случаях найти предел вида
или, иными словами, раскрыть неопределенность.
В ряде случаев по правилу Лопиталя удается раскрыть неопределенности вида
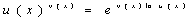 Для этого следует воспользоваться тождеством Для этого следует воспользоваться тождеством
которое приводит указанные неопределенности к виду 0•х.
13 .Производные и дифференциалы высших порядкров.
Если для функции y=f(x) определена производная у(к-1) порядка (к-1),
то производную у(к) порядка к (при условии ее существования)
определяют как производную от производной порядка (к-1), т.е. у(к) =
(у(к-1))′ . В частности, у’’=(y’)’- производная второго
порядка, y’’’=(y’’)’ – третьего и т.д.
При вычислении производных высших порядков используют те же правила, что и
для вычисления у’.
Табл. Произ-х высшего порядка:
| f(x) | fn(x) | Xa Ex Ekx Akx Lnx Logax Sinkx Cos kx | A(a-1)*(a-2)*.*(а-n+1)*х a-n Ех Kn*ekx (K* Lna)n*akx (-1)n-1*(n-1)!/xn (-1)n-1*(n-1)!/(xn*lna) kn*sin(kx+n*π/2) kn*cos (kx+n*π/2) |
Дифференциалы высших порядков ф-и y=f(v) последовательно определяются таким
образом:
d2y=d(dy) – диф-л 2-го порядка
d3y=d(d2y).
dny=d(d n-1 y) - диф-л n-го порядка
Если ф-я y=f(v), где v – независимая переменная или линейная ф-я v=кх+в
переменной х, то d2y=y’’(dv)2, d3y=y’’’(dv)
3,., dny=y(n)(dv)n.
Если же y=f(v), где v=g(x)≠кх+в, то d2y=f’’(v)*(dv)2
+ f’(v)d2v и т.д. (т.е. св-во инвариантности не выполняется).
14 Формула Тейлора.
Пусть функция f(x) имеет n производных в точке x0. Многочлен
T(x) = f(x0) + ( (f’(x0))/1! )(x – x0)1
+ (f ”(x0))/2!(x – x0)2 +.+ (f (n)
(x0))/n!(x – x0)n
Называется n-м многочленом Тейлора функции f(x) в точке x0.
Пусть функция f(x) имеет в ε – окрестности точки x0 (n + 1)
производных. Тогда для любой точки х из этой окрестности найдется точка с,
расположенная между точками х и х0, для которой выполняется
следующая формула
F(x) = T(x) + ( f(n+1)(c) / (n + 1)!)(x – x0)n+1 – формула Тейлора,
где Т(x) – n-й многочлен Тейлора функции f(x) в точке х0,
rn(x) = ( f(n+1)(c) / (n + 1)!)(x – x0)n+1 – остаточный член в формуле Лагранжа.
Предположим, что (n+1)-я производная функция f(x) ограничена в окрестности точки
х0. Тогда rn(x) является бесконечно малой более высокого
порядка, чем (х-х0)n при х ® х0. (lim (rn
(x)/(х-х0)n) = lim [((f(n+1)
(c))/(n+1)!)(x-x0)] = 0 – в силу
Х®Хо Х®Хо
Ограниченности f(n+1) (c) в окрестности х
0.) Следовательно ошибка в приближенном равенстве f(x) » Tn(x)
(*) также является бесконечно малой более высокого порядка, чем (х – х0
)n, когда х ® х0.
Формула (*) применяется для приближенных вычислений.
Используя равенство (*) можно подучить, например следующие формулы (при х®0):
1) (1+x)a » 1 + (a/1!)x + (a(a-1)/2!)x2 +.+ (a(a-1).(a-n+1)/n!)xn,
2) ex » 1 + x/1! + x2/2! +.+ xn/n!,
3) ln(1+x) » x – x2/2 + x3/3 – x4/4 +.+(-1)n+1xn/n
4) sin x » x – x3/3! + x5/5! – x7/7! +.+(-1)kx2k+1/(2k+1)!,
5) cos x » 1 – x2/2! + x4/4! – x6/6! +.+(-1)kx2k/(2k)!,
где в каждом случае ошибка является бесконечно малой относительно хn.
15 Условия монотонности функции.
Если у=f(x) непрерывна на [a,b] и дифференцируема на этом отрезке, то
у=f(x)-const, тогда и только тогда, когда f¢(x)=0 при "х'[a,b]. Следствие
у=f(x), y=g(x) непрерывна и диффиренцируема на (a,b) и f¢(x)=g¢(x),
то f(x)=g(x)+C.
y=f(x) возрастает на Х, если для любых х1,х2'Х,
таких что х1<x2Þ f(x1)<f(x2
), убывает если x1<x2Þ f(x1
)>f(x2).
Достаточное условие монотонности. Если функция непрерывна,
дифференцируема на (a,b) и внутри (a,b) сохраняет знак, то функция у=f(x)
монотонна.
Докажем для f¢(x)>0 Þ y=f(x) – возрастает на (a,b) (для убывающей
функции доказательство аналогичное)
Доказательство.
Возьмём точки из отрезка (a,b) х1 и х2, такие что х1
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
| 


