полный дифференциал определяется равенством dz=z¢xDx+z¢

yDy. Следует помнить, что в различных точках (х0, у0

) дифференциал будет различным.

Функция называется дифференцируемой в точке (х0, у0

), если её полное приращение можно представить в виде Dz=f(x,y)- f(х0

, у0)=fx¢(х0, у0)Dx+fy

¢(х0, у0)Dy+ep или, короче, Dz=dz+ep, где e=e(Dх, Dу)

– функция бесконечно малая при Dх® 0,Dу®0;

Геометрический смысл.

.

р=Ö(Dх)2+(Dу)2 - расстояние от точки (х,у) до точки (х0,у0).

Дифференцируемость функции z=f(z,y) в точке (х0,у0)

предполагает наличие производных z¢x и z¢y в

этой точке. Поэтому, если хотя бы одна из указанных производных не существует ,

то функция не является дифференцируемой в точке (х0,у0).

Запишем линейный аналог уравнения, отбросив слагаемое eр:

z-f(х0,у0)=f¢x(х0,у0

)(x-x0)+f¢y(х0,у0)(y-y0

). Это уравнение в коотдинатах x,y,z задаёт плоскость, которая называется

касательной плоскостью к графику функции f(x,y) в точке (М(х0,у

0), f(х0,у0)).

(можно доказать, что для любой последовательности точек {N1,N2

,.}, принадлежащих графику функции z=f(x,y) ( и отличных от М), угол между

прямой MN1 и касательной плоскостью стремится к нулю.

(Теорема Если функция z=f(x) дифференцируема в точке (х0

,у0), то она непрерывна в этой точке.)

3. Производная по направлению. Градиент.

Пусть l=(lx;ly) – произвольный единичный вектор, т.е. такой вектор, что

.

|l|=Ölx2+ly2=1

Производной функции f(x,y) в точке (х0,у0) по

направлению вектора l называется предел df(х0,у0)

=lim f(х0+tlx,у0+tly)- f(х0

,у0)

dl t®0+0 t

Говорят также, что df(х0,у0)/dl – это скорость изменения

функции в точке (х0,у0) в направлении вектора l.

Градиентом функции в точкеМ называется вектор, координаты которого

равны соответствующим частным производным данной функции в точке М.

Пример для функции от двух перменных. f(x,y) grad f(M)=(fx¢(M);fy¢(M)).

Градиент можно записать короче. df(M)(grad f(M),l)

dl

где (grad f(M),l) – скалярное произведение векторов.

[(grad f(M),l)=|grad f(M)|*|l|cosj, l – единичный вектор] Ни количество

аргументов функции f, ни длина вектора l не играет существенного значения при

выводе формулы.

Вывод.Градиент указывает направление наискорейшего роста функции, а

максимальная скорость роста равна модулю градиента.

4 Однородные функции. Формула Эйлера.

Опр. Пусть D Ì Rn – область в Rn,

содержащая вместе с каждой своей точкой (х1, х2,., х

n) и все точки вида (tх1, tх2,., tхn) при

t >0. Функция f(х1,., хn) c такой областью определения

D называется однородной степени a, если для любого t >0

выполняется равенство: f (tх1,., tхn)= t

a f (х1,., хn).

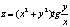Степень однородности a может быть любым действительным числом. Например,

функция является однородной функцией степени 2π от переменных х и у.

Предположим, что дифференцируемая функция f (х, у) является одновременно

и и однородной функцией степени a. Фиксируя произвольную точку (х, у) для

любого t >0, имеем

f (tх, tу)= ta f (х, у). Продифференцируем левую и

правую части этого равенства по t (левую часть - по правилу диф-я сложной

функции, правую часть – как степенную функцию). В результате приходим к

тождеству:

f 'x (tх, tу)х+ f 'y (tх, tу)y =a ta-1 f (х, у)

Положив t=1 , получим формулу Эйлера:

f 'x (х, у)х+ f 'y (х, у)y =a f (х, у)

Аналогично записывается формула Эйлера для однородной функции от

любого числа аргументов. Например, для функции трех переменных она выглядит

следующим образом:

f 'x (х, у,z)х+ f 'y (х, у,z)y + f 'z (х, у,z)z =a f (х, у, z) или

и 'x x + и 'y y+ и 'z z=a и (*)

Предположим, что функция и= f (х, у,z) не обращается в 0 в некоторой

точке (х0, у0,z0). Разделив тогда левую и

правую части равенства (*) на значение функции в этой точке, получим формулу:

Е их + Е иу + Е иz=a

где Е их, Е иу., Е иz – коэффициенты эластичности и по

х, по у, по z в точке (х0, у0,z0

).

5. Производственные функции и функции полезности. Изокосты, изокванты и

Производственные ф-и – экономико-математическое уравнение,

связывающее переменные величины затрат (ресурсов) с величинами продукции

(выпуска). ПФ может устанавливать зависимость объема продукции от наличия или

потребления ресурсов – ф-я выпуска, наряду с которыми исп-ся

как бы обратные к ним ф-и зависимости затрат рес-в от объемов выпуска

продукции. Частными случаями ПФ. Явл. ф-я издержек (связь объема продукции и

издержек пр-ва), ф-я капитальных затрат (завис-ть капиталовложений от

производственной мощности предприятия). Наиболее важные из мат. Форм ПФ:

Линейная ПФ: Р=а1х1+а2х2+.+аnxn, где а1, а2,.. - факторы пр-ва.

Ф-я Кобба-Дугласа: N=A*Lα*Kβ , где N-

национальный доход страны, L и K- соответственно объемы приложенного труда и

капитала.

Ф-я CES: P=A[(1-a)K-b +aL-b] -c/ b

Ф-я полезности показывает зависимость эффекта некоторого действия

от интенсивности этого дей-я. Общий вид: u=u(x1,.xn), x

1,.xn- факторы, влияющие на полезность u. ФП может

служить моделью поведения потребителей благ и услуг в обществе и

рассматриваться как целевая ф-я потребления: v=v(с1,.сm),

с1,.- количества благ. Потребители стремятся максимизировать эту

ф-ю. Мат. Св-во ф-и: она должна иметь положительную первую производную, что

означает: при увеличении объема благ увеличивается и полезность. Выбирая между

разными наборами благ потребитель предпочтет те, чья полезность больше, поэтому

ФП часто наз ф-й предпочтений.

Изокосты – геометрическое место точек (в пространстве ресурсов),

для которых издержки пр-ва постоянны. В случае двух видов затрат И.

Представляют собой параллельные прямые с наклоном, который равен отношению цен

к затратам каждого вида (взятому с отрицательным знаком), что вытекает из

формулы издержек: С=р1х1+р2х2,

р1,р2 – цены, х1,х2 – объемы затрат каждого вида.

Х2

1 2 Х1

Изокванта – геометрическое место точек, в которых разные сочетания

факторов пр-ва (ресурсов) дают одно и то же кол-во выпускаемой продукции.

Кривизна И. Характеризует эластичность замещения между затратами этих факторов.

Вид изокванты для двух видов взаимозаменяемых ресурсов:

Х2 q1

Х22 q2

Х21 q1

Осн. Св-ва:

1) Никогда не пересекаются друг с другом

2) Большему выпуску продукции соответствует более удаленная от начала

координат изокванта

3) Если все ресурсы абсолютно необходимы для произ-ва, то И. Не имеют

общих точек с осями координат,

4) При увеличении затрат одного ресурса объем произ-ва можно

сохранить на том же уровне при уменьшении затрат др. рес.

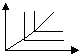В случае отсутствия возможности

замены рес-в И. Приобретают вид (рис. 1) при постоянном соотношении затрат и

при изменяющемся соотношении затрат (рис.2)

Х2 Х2

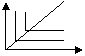
Х1 Х1

Рис.1 Рис2

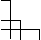
Кривые безразличия – геометрическое место точек ( пространства товаров),

характеризующихся состоянием безразличия с точки зрения потребителя или

производителя. Это графическая иллюстрация взаимозаменяемости товаров.

Применяется для анализа спрса и потребления, а также др. эк. Явлений.

Отложим по оси 0Х кол-во 1-го блага, ОУ-другого. Кривая безразличия соединяет

все толчки, отражающие такие комбинации, что покупателю безразлично, что

покупать.

Если построить много кривых безразличия, то получится карта безразличия.

Св-ва:

1) К.Б. имеют отрицат. Наклон, крутизна которого показывает

предельную норму замещения 1-го товара дру-гим.

2) Кривые никогда не пересекаются

3) Кривые выпуклы к началу координат (их абсолютный наклон

уменьшается при движении по ним вправо).

У c

y1

У2 А

Y3

Х1 Х2 Х3 Х

6. Неявные функции

Пусть переменная u, является функцией переменных х1, х2,.,

хn, задается посредством функционального уравнения F (х1,

х2,., хn, u) = 0. В этом случае говорят, что u как

функция аргументов х1, х2,., хn задана неявно,

а саму функцию u называют неявной функцией. Неявные функции могут задаваться и

посредством системы функциональных уравнений.

Производная функции y = y(x), заданной неявно уравнением F(x,y) = 0, где

F(x, y) – диффиренцируемая функция переменных x и y, может быть вычислена по

формуле: y’ = - F’x / F’y

При условии, что F’y ≠ 0.

Аналогично частные производные неявной функции двух переменных u =

(х1, х2), заданной с помощью уравнения F(х1, х

2, u) = 0, где F(х1, х2, u) – дифференцируемая

функция переменных х1, х2, u могут быть вычислены по

формулам: ∂u / ∂x1 = - F’x1 / F’u, ∂u /

∂x2 = - F’x2 / F’u.

7. Теоремы существования решений системы функциональных уравнений.

Пусть m функций

F1(х1,., хn , u1,., um);

F2(х1,., хn , u1,., um);

.........

Fm(х1,., хn , u1,., um)

Дифференцируемы в некоторой

окрестности точки a = (х10,., хn0,

u10,., um0) евклидова пространства

Rn+m, причем частные производные этих функций

по переменным u1,., um непрерывны в точке a. Тогда если

все функции F1,.,Fm обращаются в нуль в точке a, якобиан

D(F1,.,Fm) / D(u1,.,um) отличен от

нуля в этой точке, то найдется окрестность точки (х10, х

20,., хn0), в которой существует

единственные m функции u1 = f1(х1, х2

,., хn), u2 = f2(х1, х2

,.,хn), ., um = fm(х1, х2

,., хn), являющиеся решениями системы

F1(х1,., хn , u1,., um) = 0;

F2(х1,., хn , u1,., um) = 0;

.........

Fm(х1,., хn , u1,., um) = 0,

Причем это решение непрерывно и дифференцируемо в указанной окрестности точки (х

10,., хn0). При этом

∂fk / ∂xj = - D(F1,.,Fm)

/ D(u1,.,uk-1, xj, uk

+1,., um) : D(F1,.,Fm) / D(u1,.,um

).

Выражения для частных производных второго и последующих порядков, при условии

их существования, можно получить посредством дифференцирования этих формул.

8. Теоремы существования решений функционального уравнения.

Пусть функция F(х1, х2,., хn , u) непрерывна на

области D евклидова пространства Rn+1, F(х1

0, х20,., хn 0, u0)

= 0; (∂F / ∂u) (х10, х20

,., хn 0, u0) ≠ 0 (точка (х1

0, х20,., хn 0, u0)

Î D). Тогда существует окрестность указанной точки, в которой уравнение

F(х1,., хn , u) = 0 однозначно разрешимо, причем решение

u = f(х1, х2,., хn ) непрерывно в этой

окрестности. Если, кроме условий, оговоренных выше, функция F дифференцируема в

окрестности точки (х10, х20,., х

n 0, u0) и ∂F / ∂u непрерывна в этой

точке, то решение u = f(х1, х2,., хn

) дифференцируемо в окрестности рассматриваемой точки, причем ∂f /

∂xk = - ∂F / ∂xk : ∂F /

∂u, k = 1,2,.,n.

Частные производные второго и более высоких порядков, при условии их

существования, могут быть найдены посредством дифференцирования формул для

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12