|
частных производных первого порядка.
9 Экстремумы функций нескольких переменных. Необходимое условие экстремума.
Достаточное условие экстремума.
Точка М0 называется точкой локального максимума (минимума)
функции f(x,y), если существует такая окрестность точки М0, в которой
для любой точки М(х,у) выполняется неравенство f(M)£f(M0)
(f(M)³f(M0)).
Точки локального экстремума называются просто точками экстремума.
Необходимое условие существования экстремума.Если функция f(x,y)
имеет частные производные первого порядка в точке локального экстремума М
0(х0,у0), то f¢x(M0
)=f¢y(M0)=0.
Доказательство.Рассмотрим сначала функцию одной переменной f(x,y0
). Производная этой функции совпадает с частной производной f¢x
(x,y0), а сама функция имеет локальный экстремум в точке х0
. Следовательно, производная функция f(x,y0) в точке х0
равна нулю, т.е. f¢х(x,y0)=0. Аналогично функция от
одной переменной f(x,y0) имеет локальный экстремум в точке у=у0
. Следовательно, её производная в этой точке равна нулю, т.е. f¢у
(x,y0)=0.
Равенство частных производных нулю выражает лишь необходимое, но не
достаточное условие существования экстремум.
Точки, в которых частные производные равны нулю или не существуют, называют
критическими точками.
Достаточное условие существования экстремума. Пусть функция f(x,y)
имеет непрерывные частные производные второго порядка в некоторой окрестности
стационарной точки М0(x0,y0). Положим D=
f¢¢xx(M0)f¢¢yy(M0
) – (f¢¢xy(M0)2. тогда :
1. если D>0, то в точке М0 функция имеет локальный
экстремум, причём f¢¢xx(M0)<0 – локальный
максимум, при f¢¢xx(M0)>0 – локальный
минимум;
2. если D<0, то в точке М0 нет экстремума.
3. если D=0, то требуются дополнительные исследования.
(в лекциях 2-го семестра доказательства не приводилось, если есть большая
тяга к знаниям, то см учебник стр 182-185).
10. Наибольшее и наименьшее значения функции на ограниченном замкнутом
множестве.
Схема исследования функции на экстремум.
1. z¢x, z¢y
2. Найти критические точки. z¢x=0, z¢y=0
3. Взять производные z¢¢xx,z¢¢yy,z¢¢xy,z¢¢yx.
4. C помощью условия существования экстремум сделать вывод.
Теорема Вейерштрасса.Если функция z=f(x,y) непрерывна на
замкнутом, ограниченном множестве, то на этом множестве функция принимает
наибольшее и наименьшее значение.
Правило нахождения максимума и минимума для функции от двух переменных.
1. Найти ОДЗ и обедиться, что оно замкнутое и ограниченное.
2. Исследовать на экстремум, вычислить значение функции.
3. Вычислить значения функции на границах ОДЗ.
4. Из всех значений выбрать наибольшее и наименьшее.
11. Метод наименьших квадратов.
(рассмотрим для двух величин, остальные аналогично0Пусть (Х,У) – система двух
случайных величин. Задача – исследовать связь между Х и У.
М(У/Х=х) – условные математические ожидания случайной величины У при условии,
что Х=х (х – фиксированное число) М(У/Х=х)=f(x). Уравнение y=f(x) называется
уравнением регрессии СВ У на СВ Ч. Будем приближать функцию y=f(x) к прямой
y=kx+b, т.е. попытаемся подобрать k,b так, чтобы y=kx+b как можно лучше
апроксимировать функцию y=f(x). В качестве прямой y=kx+b предлагается выбрать
ту, на которую лучше всего «ложаться» экспериментальные точки. у1=kx
1+b Þ Е21= (y1-(kx1+b))
2 характеризует степень удалённости точки (х1,у1) от
прямой y=kx+b Е22= (y2-(kx2+b))
2 и т.д. Естественный критерий, характеризующий близость всей совокупности
точек к прямой y=kx+b К=åni=1E2i
. К=к(к,b) – функция двух переменных. Найдём такие к*,b*,
которые минимизируют значение К.
К(к,b)= åni=1(yi-(kxi+b))2 Необходимое условие экстремума. DК/Dк=0; DК/Db=0
DК/Dк=åni=12(yi-(kxi+b))(-хi)=0
kåni=1 хi2+båni=1 хi =åni=1 хi yi ;
DК/Db=åni=12(yi-(kxi+b))(-1)=0
åni=1 yi -kåni=1 хi-nb=0.
íì kåni=1 хi2+båni=1 хi =åni=1 хi yi
î kåni=1 хi+nb=åni=1 yi
cистема двух линейных уравнений с двумя неизвестными к и b.
12. Выпуклые функции в Rn и их свойства.
Отрезок в Rn с концами a, b Î Rn – это множество точек
х (t)= (1-t) a + t b,
где t произвольное число из промежутка [0; 1]. Отрезок с концами a, b
обозначается [ a, b ]. Отрезок [ a, b ] совпадает с множеством точек в Rn
, представимых в виде с = aа + bb , где a,b - произвольные неотрицательные числа
такие, что a+b=1. Множество Р Ì Rn называется выпуклым
, если вместе с любыми двумя точками a, bÎР оно содержит и весь отрезок [
a, b ]. Функция n переменных f (х), определенная на выпуклом множестве
РÌRn , называется выпуклой, если для любых двух точек
a, b Î Р и любых двух чисел a,bÎ[0; 1] таких, что a+b=1,
выполняется неравенство
f (aа + bb) ≤ a f (а) + b f (b)
Для непрерывной функции, заданной на выпуклом множестве Р , следующие условия
равносильны:
1) f выпукла;
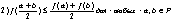
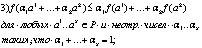
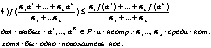
Неравенство из пункта 4 называется неравенством Йесена. выпуклая функция наз.
строго выпуклой, если неравенство f (aа + bb) ≤ a f
(а) + b f (b) строгое при всех a, b из области определения
функции и α,β ≥0 таких, что α+β=1.
Функция f наз. (строго) вогнутой, если –f (строго) выпукла, т.е.
f (aа + bb) ≥ a f (а) + b f (b)
Линейная функция f(x)=(c,x)+c0 одновременно выпукла и вогнута, но не строго.
Свойства выпуклых функций.
1. функция с выпуклой областью определения Р Ì Rn
выпукла тогда и только тогда, когда выпукло множество Нf
={(х,у):хÎР, у≥f(x)} (из Rn+1)
называемое надграфиком функции f(x).
2. Если f(x) выпукла, то функция αf(x) выпукла при
α>0 и вогнута при α<0.
3. Если f(x) выпукла на Р, то множество Uf
(α)={х:f(x) ≤α} выпукло при любом α.
(обратное утверждение неверно).
4. Сумма любого числа выпуклых функций на множестве Р Ì Rn
выпуклана Р , если при этом хотя бы одна из суммируемых функций строго выпукла,
то вся сумма строго выпукла.
5. Пусть Р Ì Rn – выпуклое множество, и для каждого
i=1,2,.k пусть li(x) – линейная функция n переменных , а
fi(t) – функция одной переменной , выпуклая на li
(Р). Тогда функция F(х)=f1 ( l1(x))+.+ fК
( lК(x)) выпукла на Р. При этом, если все функции fi
(t) строго выпуклы и любая точка однозначно определяется набором ( l
1(а)+.+ lК(а)), то F(х) строго выпукла.
6. Пусть f выпукла на Р Ì Rn , а φ(t) –
возрастающая выпуклая функция на множестве f(Р) ÌR, тогда
F(х)= φ(f(x)) выпукла на Р. Если f(x) строго выпукла, то и F(х)
строго выпукла.
7. Дифференциируемая функция f(x) выпукла на множестве Р
Ì Rn тогда и только тогда, когда (grad f(a), b-a)
≤f(b)-f(a) для любых a,bÎР
8. Пусть f(x) – функция, непрерывная на отрезке [ a, b
]ÌR и дважды дифференциируемая на (a, b). Для выпуклости функции f
(x) на [ a, b ] необходимо и достаточно выполнение неравенства f˝
(x)≥0 для всех tÎ (a, b). Для строгой выпуклости f(x)
добавляется условие f˝(x)≠0 ни на одном интервале,
содержащемся в (a, b).
9. 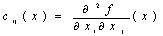 Пусть D – Пусть D –
выпуклое открытое множество в пространстве Rn, f(x)=f
(x1,.,хn) – функция, имеющая в D непрерывные частные
производные второго порядка. Для каждой точки хÎ D положим
и составим матрицу
C=Cij(X). Функция f(x) строго выпукла на множестве D , если в каждой
точке хÎ D выполняются следующие неравенства
∆1=с11>0,
., ∆n=det
c>0
Экстремальные значения выпуклых и вогнутых функций.
1.Если х* - точка локального минимума (максимума) выпуклой (вогнутой) функции
f(x) на выпуклом множестве Р Ì Rn то f(x*) –
наименьшее (наибольшее) значение f(x) на Р. Если f(x) строго
выпукла (вогнута), то х* - единственная точка глобального экстремума.
2.Пусть f(x) – выпуклая (вогнутая) функция на выпуклом множестве Р
Ì Rn и пусть grad f(x*)=0. Тогда х* -точка
глобального минимума (максимума) f(x) на Р.
13. Множители Лагранжа и теорема Куна-Таккера.
рассмотрим следующую задачу, называемую задачей вогнутого программирования:
найти точку глобального максимума вогнутой функции f(x) на выпуклом
множестве Р Ì Rn , заданном системой неравенств:
ó g1(x)³0,
î ....
ì g s(x)³0
ì g s(x)³0
î x³0
где g1(х),., g s(x) – вогнутые функции. для решения
вводят функцию Лагранжа F(x,l)=f(x)+l1 g1(x)+.+l
s g s(x), где l=(l1,.,l s) –
вектор множителей Лагранжа. Предположим, что все функции дифференциируемы и
существует точка х³0, для которой все тривиальные неравенства из системы
уравнений строгие. Точка х*³0 является точкой глобального максимума f
(x) на Р в том случае, когда существует вектор l*=(l*1,.,
l*s)³0, такой, что выполняются условия:
gradxF(x*, l*)£0;
(gradxF(x*, l*);х*)=0
gradlF(x*, l*)³0
(gradlF(x*, l*);l*)=0
Эти условия означают, что точка (x*, l*) является седловой точкой
функции F(x, l), т.е. F(x, l*)£ F(x*, l*)£ F(x*, l)
5. Числове и функциональные ряды. 1. Числовые ряды. Сходимость и
сумма ряда. Необходимое условие сходимости. Действия с рядами.
Числовым рядом наз-ся бесконечная последовательность чисел, соединенная
знаком сложения: а1+а2+.+ак +.=∑к=1∞ак.
Где а1,.,ак- члены числового ряда
Введем след. Обозначения: Sк = ∑к=1каi = а1+а2+.+ак
- n-ая частичная сумма числового ряда: к=1, то Sк=а1,к=2, то Sк=а1+а2,.к: Sк
= а1+а2+.+ак, т.е. видно, что частичная сумма образует числ.
Последовательность.
Числ ряд наз сходящимся, и его сумма в этом случае будет равна S, если сущ-т
конечные предел последовательности частичных сумм, котрый равен S: LimSk=S,
k→∞. В противном случае числ ряд расходится.
Св-ва сходящихся числ. Рядов.
Рассмотрим 2 числ ряда:
а1+а2+.+ак +.=∑к=1∞ак. (1)
в1+в2+.+вк +.=∑к=1∞вк ( 2)
Опр.
1).Суммой этих рядов наз ряд. Каждый член которого равен сумме
соответствующих членов рядов (1) и (2).
2) Ряд , каждый член которого равен произведению соответствующего члена ряда
(1) на одно и то же действительное число, наз произведением ряда на
действительное число λ.
Св-ва.
1)Если ряд (2) сходится, и его сумма равна S, тогда произведение этого ряда
на действительное число также сходится, и его сумма будет равна λS.
Док-во: Пусть Sk- частичная сумма ряда (2), sk - частичная сумма ряда
λ в1+ λ в2+.+λ вк +., ясно, что λ Sk = sk. Переходя к
пределу, получим:
Lim sk=lim λSk= λlimSk= λS(k→∞)
2)Если ряды (1) и (2) сходятся, и их суммы соответственно равны S, S’, то ряд
из определения 1) (назовем его (3)) также сходится, а его сумма будет равна
S+S’.
Док-во: Qk=Sk+Tk, где Qk, Sk,Tk – сответственно частич суммы рядо (1), (2),
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
| 


