иррациональных и трансцендентных функций.

(конкретные числовые примеры по данному вопросу см. в лекции за 21.03.00)

Рассмотрим интегал вида òR(x)dx, где R(x) – рациональная функция, т.е

функция, которую можно представить в виде отношения двух многочленов

R(x)=P(x)/Q(x). Если эта дробь неправильная, то можно выполнить деление с

остатком и представить R(x) в виде суммы некоторого многочлена и правильной

дроби.

Теорема. Всякая правильная дробь может быть представлена как сумма

простейших дробей вида

A ; A ; Mx+N ; Mx+N .

x-a (x-a)n x2+px+q (x2+px+q)n

, где A,M,N,a,p,q – действительные числа.

Непростейшие дроби.

Лемма 1. Пусть F(x)/Q(x) – правильная дробь. Если х=а- корень Q(x)

кратности К,т.е. Q(x)=(x-a)K*Q1(x), где Q

1(a) не равно нулю, то F(x)= AK+

F1(x)

Q(x) (x-a)K Q1(x)*(x-a)K-1

Лемма 2. Пусть F(x)/Q(x) – правильная дробь. Если Q(x)=(x2+px+q)K*Q1(x) Þ

F(x) =MKx+NK + F1(x) .

Q(x) (x2+px+q)K (x2+px+q)K-1*Q1(x)

Теорема разложения правилоной дроби на простейшие. Пусть F(x)/Q(x)

– правильная дробь. Если Q(x)=(x-a)a(x-b)b*.

*(x-c)g(x2+p1x+q1)K

*.*(x2+p2x+q2)m

Þ эта дробь разлагается в сумму простейших дробей следующего вида:

F(x) = Aa+ Aa-1+.+ A1+ Bb+ Bb-1+.+ B1+ Cg+ Cg-1+.+ C1+

Q(x) (x-a)a (x-a) a-1 x-a (x-b)b

(x-b) b-1 x-b (x-c)g (x-c) g

-1 x-c

+ MKx+NK + MK-1x+NK-1+.+ M1x+N1+ Cmx+Dm + Cm-1x+Dm-1+.+ C1x+D1

(x2+p1x+q1)K (x2+p

1x+q1)K-1 x2+p1x+q

1 (x2+p2x+q2)m (x2

+p2x+q2)m-1 x2+p2x+q

2

Интегрирование иррациональных и трансцендентных функций.

Трансцендентная функция – аналитическая функция, не являющаяся

алгебраической. (Например, показательная функция тригонометрической функции.)

òR(x,xm1/n1,.xmk/nk)dx, где R – рациональная

функция от х и её дробных степеней. Такой интеграл может быть решён с помощью

замены степени с дробным показателем на степень функции с целым показателем.

(подробнее см. в лекциях)

.

òR(x,ÖAx2+Bx+C )dx Под корнем выделяется полный квадрат

и решается с помощью замены переменной.

. .

òdx/Ö Ax2+Bx+C , òÖ Ax2+Bx+C dx

Теорема. Пусть функция у=f(х) непрерывна на

отрезке [а, b] и F(х) – первообразная для f(х).Тогда

(*)

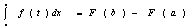
Доказательство: Поскольку функция f(х) непрерывна

на отрезке [а, b], то она интегрируема на этом отрезке и имеет первообразную на

этом отрезке. Проверим справедливость формулы (*). Действительно,

подставляя х=b, получим

а подставляя х=а, получим

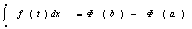
поэтому

Если F(х) – другая первообразная для функции f(х), то выполняется

равенство F(х)= Ф(х)+С. Имеем

F(b)-F(a)=(Ф(b)+C)-(Ф(а)+С)=Ф(b)-Ф(а)

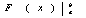что завершает доказательство

формулы (*). Разность F(b)-F(a) часто записывают в виде

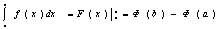и формула Ньютона-Лейбница в этом случае принимает следующий вид:

(**)

Мы доказали формулу для случая, когда f(х) непрерывная на [а, b]

функция. В действительности эта формула справедлива для любой функции f(х)

, имеющей первообразную F(x)/

Формулу (**) обычно называют основной формулой интегрального исчисления. она

позволяет сводить нахождение определенного интеграла к нахождению

первообразной.

7. Несобственые интегралы с бесконечными пределами.

Пусть y=f(x) определена и непрерывна на промежутке [a;+∞], интегрируема

на любом [a;b] (b>a). Сущ-т ∫ab f(x)dx для

любого b>a. Обозначим ∫ab f(x)dx = Ф(b).

Несобственным интегралом с бесконечным верхним пределом от ф-и y=f(x) мы

назовем предел вида ∫a∞ f(x)dx=lim Ф(b) при

b→+∞. Этот инт-л наз. Сходящимся, если предел ф-и

lim Ф(b) при b→+∞ сущ-т и конечен. В противном случае он наз

расходящимся.

Аналогично определяем несобственный инт-л с бесконечным нижним пределом

. Пусть y=f(x) определена и непрерывна на промежутке (-∞;в],

интегрируема на любом [a;b] (a<b). Сущ-т ∫ab

f(x)dx для любого a<b, Обозначим ∫ab f(x)dx =

Ф(a), ∫-∞b f(x)dx = lim Ф(a) при

а→–∞. Этот инт-л наз сходящимся, если предел сущ-т и конечен, в

противном случае – расходящимся.

Несобственный инт-л с бесконечными нижним и верхним пределами.

∫-∞∞ f(x)dx

y=f(x) опред-на и непрерывна на (–∞;∞) и интегрируема для любого

[а;b]. Возьмем произвольную точку с на (–∞;∞). Имеем: ∫

-∞∞ f(x)dx = ∫-∞с

f(x)dx + + ∫с∞ f(x)dx (1)

Если сущ-т несобственные интеграл с бесконеч. Верхним пределом и несоб. Инт-л

с бесконечным нижним пределом, и они оба сходятся, то сходится и

несобственный интеграл с бесконечным верхним и нижним пределом. В этом случае

сумма (1) не зависит от выбора точки с.

Геометрич. смысл несобственного интеграла.

Пусть y=f(x) неотрицат. Непрерывная на [a;b). Для каждого b>a определенный

инт-л ∫ab f(x)dx = S aABb. Мысленно перемещая Bb

вправо, получим ∫a∞ f(x)dx=SaA∞.

A

B

a b

8. Несобственные интегралы от неограниченных ф-й.

Если сущ-т интеграл ∫ab f(x)dx, то y=f(x)

ограничена (но обратно это не обязательно).

1).Опр. Точка х=в наз. Особой точкой ф-и y=f(x), если в любой

окрестности этой точки ф-я не ограничена, но ограничена на любом отрезке

[a;в-ε], ε>0.

Опр. Пусть ф-я y=f(x) не ограничена на [а;в], но интегрируема на любом

меньшем отрезке [a;в-ε], ε>0, тогда если сущ-т конечный предел

ε→0+0, то его принимают за несобственный интеграл ∫

ab f(x)dx от неограниченной ф-и f(x). Если предел сущ-т и

конечен, то инт-л сходится, в противном случае он расходится.

2).Аналогично,

Если точка а – особая: ∫ab f(x)dx = lim ∫

a+ε b f(x)dx, при ε→0+0

3). Пусть с –единственная внутренняя особая точка на [а;в]. Если сходятся

∫aс f(x)dx и ∫сb

f(x)dx, то получим несобственный интеграл ∫ab

f(x)dx (2)

Если особых точек на отрезке [а;в] несколько, то отрезок разбивают, чтобы в

каждом получившемся отрезке было не более одной особой точки и используют

(2).

Пусть F(x) – первообразная для y=f(x), F(a+0)=lim

F(a+ε),ε→0+0, F(b-0)=lim F(b-ε),ε→0+0 (если

эти пределы сущ-т). Тогда:

∫ab f(x)dx= F(b-0)- F(a+0)

Если y=f(x) непрерывна, то ∫ab f(x)dx= F(b)- F(a)

4. Дифференциалльное исчисление функций нескольких переменных.

1

Множество в Rn: открытые, замкнутые, ограниченные, выпуклые.

Компактность. Функции нескольких переменных. Предел и непрерывность функции.

Функции, непрерывные на компактах. Промежуточные значения непрерывных функций

на линейно связных множествах.

Пусть р0 – точка в Rn и ε – положительное число.

Открытым шарам или просто шаром радиуса ε с центром в точке р

0 называется множество всех точек, расстояние которых от р0

меньше ε.

ρ(p0, p) < ε.

Множество X Ì Rn называется ограниченным, если оно

целиком содержится в некотором шаре.

Пусть Х – множество в пространстве Rn. Точка р Î Х называется:

внутренней точкой множества Х, если существует шар B(p,r), все точки

которого принадлежат Х;

внешней точкой по отношению к Х, если существует шар B(p,r), ни одна

точка которого не принадлежит Х;

граничной точкой для Х, если она не является ни внутренней, ни внешней

точкой Х, иначе говоря, если любой шар с центром р содержит как точки,

принадлежащие Х, так и точки, не принадлежащие Х

Множество Х называется открытым, если его точки внутренние. Множество Х

называется замкнутым, если оно содержит все свои граничные точки.

Выпуклое множество – часть плоскости, обладающая тем свойством, что

соединяющий две любые точки отрезок содержится в ней целиком.

Пусть Х – множество в Rn. Точка р0 называется

предельной для Х, если в любой окрестности точки р0 (любом шаре

B(p0, ε)) имеются точки множества Х, отличные от р0.

Топология – раздел математики, изучающий топологические свойства фигур,

т.е. свойства не изменяющиеся при любых деформациях, производимых без разрывов

и склеиваний. Примерами топологических свойств фигур являются размерность,

число кривых, ограничивающих данную плоскость и т.д. Так, окружность, эллипс,

контур квадрата имеют одни и те же топологические свойства, т. к. эти линии

могут быть деформированы одна в другую описанным выше способом. В то же время

кольцо и круг обладают различными топологическими свойствами: круг ограничен

одним контуром, а кольцо – двумя.

Компактность – одно из основных понятий топологии. Множество называется

компактным, если любая бесконечная последовательность его точек (элементов)

имеет хотя бы одну предельную точку, принадлежащую этому множеству. Например,

на плоскости компактными являются ограниченные, замкнутые множества и только

они.

Правило, по которому каждой точке x (x1, x2,., xn

) Î X (X Ì Rn) ставится в соответствие единственное

действительное число y Î E (E Ì R) называется функцией

n переменных.

X Ì Rn – область определения функции

E Ì R – множество значений функции.

Пусть на множестве X Ì Rn задана функция f и пусть р0

– предельная точка для Х. Число а называется пределом функции f в точке

р0, если для любой сходящейся к р0 последовательности {р

n}, где все рn ≠ pa, соответствующая числовая

последовательность {f(pn)} сходится к числу а. (lim f(p) = a)

P®Po

Функция f, определенная на множестве Х Ì Rn, называется

непрерывной в точке p0 Î X, если lim f(p) = f(p0

), а также если р0 – изолированная точка

P®Po

множества Х.

2 Частные производные. Дифференциал, его связь с частными производными.

Геометрический смысл частных производных и дифференциала.

Частной производной функции нескольких переменных по одной из этих

переменных называется предел отношения частного приращения функции к приращения

функции к приращению соответствующией независимой переменной, когда это

приращение стремится к нулю.

Величина Dz=f(x0+Dx,y0+Dy)-f(x0,y0)

(одновременное изменение величин х и у) называется полным приращением

функции z в точке (x0,y0).Так же, как и в случае одной

переменной возникает задача о приближённой замене приращения Dz( которая, как

правило, является нелинейной функцией от Dх и Dу) на линейную функцию от Dх и

Dу. Роль линейного приближения выполняет полный дифференциал функции,

который определяется как сумма произведений частных производных функций на

приращения независимых переменных. Так, в случае функции от двух переменных

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12