|
F(x) (в любой точке x)
Случайная величина x называется абсолютно непрерывной, если ее F(x)
дифференцируема в любой точке x1 за исключением, быть может,
конечного числа точек.
Свойства непрерывной случайной величины: P{x = x} = F(x+0) – F(x-0) = 0
При этом F(x) непрерывна.
15. Свойства функции плотности.
Плотность вероятности абсолютно непрерывной случайной величины есть по
определению функция f(x) = F’(x)
Свойства f(x): 1) f(x) ³ 0
2) a∫bf(x)dx = F (b) – F(a) Þ a∫bf(x)dx =P{a £ x < b}
3) -¥∫¥f(x)dx = P{-¥ £ x < ¥} = 1; -¥∫¥f(x)dx = 1 - условие нормировки
4) (вероятностный смысл f(x))
Xo∫Xo+ΔX f(x)dx = P{x0 £ x < x0 + Δx}
При Δx ® 0; Xo∫Xo+ΔX f(x)dx » f(x0
)Δx » P{x0 £ x < x0 + Δx}
16. Математическое ожидание и дисперсия непрерывной случайной величины
x - непрерывная случайная величина, x Î (-¥; +¥)
 x x x x x x x x x x
X-2 X-1 Xo X1
Введем дискретную случайную величину xЕ Î {., x-2, x-1, x0, x1, x2,.}
Закон распределения дискретной случайной величины xЕ
Pi = P{xi £ x < xi+1} = Xi∫Xi+1f(x)dx x x1 x2 .
p p1 p2 .
Математическое ожидание МxЕ = i = -¥S¥xipi = i = -¥S¥xip{xi £ x < xi+1}
По определению полагаем:
Mx = lim МxЕ = lim i = -¥S¥xi f(xi )Δxi = -¥∫¥xf(x)dx
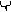 E®0 E®0 E®0 E®0
E
Итак, если x Î (a,b), то Мx = a∫bxf(x)dx; a∫bf(x)dx = 1
Дисперсия Dx = M{(x - Mx)2} = a∫b (x - Mx)2 f(x)dx
Стандартное отклонение случайной величины X определяется как корень
квадратный из диспрерсии и обозначается σx.
Для математического ожидания и дисперсии непрерывной случайной величины Х
сохраняются свойства числовых характеристик дискретной случайной величины.
17. Непрерывные распределения специального вида (равномерное, показательное,
распределение Лапласа)
Функцией распределения вероятностей случайной величины называется функция
F(x), значения которой для каждого значения аргумента х даёт вероятность того,
что случайная величина Х принимает значение, меньшее х, т.е. F(x)=P(X<x).
Если функция распределения F(x) всюду дифференцируема, за исключением, быть
может, нескольких точек, то случайная величина Х называется абсолютно
непрерывной. Тогда функцией плотности f(x) называется её производная.
Распределение вероятностей называется равномерным, если на интервале,
которому принадлежат все возможные значения случайной величины, плотность
распределения сохраняет постоянное значение.

для хÎ[a,b] f(x)=const для хÏ[a,b] f(x)=0. const=1/(b-a).
M(x)=(b+a)/2; D(x)=(b-a)2/12.s(x)=(b-a)/2Ö3
Показательным (экспоненциальным) называют распределение вероятностей
непрерывной случайной величины Х, которое описывается плотностью
f(x)= ì 0 , x<0,
íî le-lx ,x³0. График выглядит следующим образом
 М(х)=1/l. D(x)=1/l2.s(x)=1/l. М(х)=1/l. D(x)=1/l2.s(x)=1/l.
Нормальным называют распределение вероятностей непрерывной случайной
величины, которая описывается плотностью.( гауссовское распределения)
f(x)= 1* e-(x-a)^2/2s^2
sÖ2pØ нормальное распределение
определяется параметрами а и s.
Функция Лапласса. Ф(х)= 1òх е-t^2/2
Ö2p 0

вершина достигается в точке (а; 1/(Ö2pØs))
D(x)=s2; M(x)=a; s(x)= s. Среднее квадратичное отклонение нормального
распределения равно параметру s.
18. Неравенства Маркова и Чебышева. Закон больших чисел. Теоремы Бернулли и
Чебышева. Центральная предельная теорема Ляпунова.
Неравенство Маркова . Пусть У ³0 - дискретная СВ. e>0 - некоторое число,
тогда Р(У³e) ≤М(У)\ e
Неравенство Чебышева. Пусть имеется СВ x с математическим ожиданием m и
дисперсией D. Каково бы ни было положительное число e, вероятность того, что
величина x отклонится от своего математического ожидания не меньше чем на e,
ограничена сверху числом D\e2
Под законом больших чисел в теории вероятностей понимается ряд теорем, в
каждой из которых устанавливается факт приближения средних характеристик
большого числа опытов к некоторым определенным постоянным.
Теорема Чебышева. Пусть имеется бесконечная последовательность x1,x2,..
независимых случайных величин с одним и тем же математическим ожиданием m и
дисперсиями, ограниченными одной и той же постоянной:
M[x1]=M[x2]=.=m
D[x1]<c, D[x2]<c,.
Тогда каково бы ни было положительное число e, вероятность события
|((x1+.+xn)\n)-m|<e, стремится к 1 при n стремящемся к бесконечности.
Теорема Бернулли. Пусть производится n независимых опытов, в каждом из
которых с вероятностью р может наступить некоторое событие А. Рассмотрим СВ n
- число наступлений события А в n опытах. Каково бы ни было положительное
число e, вероятность события
|n\n-p|<e стремится к 1 при n стремящемся к бесконечности.
Центральная предельная теорема Ляпунова.
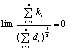 Если последовательность Если последовательность
x1,x2,..независимых СВ удовлетворяет условию Ляпунова (отдельные отклонения xi
от ее математического ожидания должны быть равномерно малы по сравнению с
суммарным отклонением случайных величин. Если при n стремящемся к бесконечности
предел
то будем говорить, что последовательность
x1,x2,..удовлетворяет условию Ляпунова)
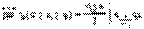 то справедливо предельное соотношение то справедливо предельное соотношение
что означает, что закон распределения СВ v' с ростом приближается к
нормальному с мат. ожиданием 1 и дисперсией 0.
8. Математическая статистика. 1. Генеральная совокупность и
выборка. Вариационный ряд. Гистограмма,
Опр.1. Выборкой наз совокупность случайно отобранных объектов.
Опр.2 Генеральной совокупностью наз совокупность объектов, из которых
производится выборка. Объемом сов-ти наз число объектов этой совокупности.
Опр.3. Ряд распределения – это упорядоченное распределение единиц совокупности
на группы по к.-л. признаку. Вариационным рядом (в.р.) наз группировка
сов-ти по количественному признаку, т.е. это ряд распределения, сгруппированный
по колич. Признаку.
В.Р. будет дискретным, если он остроен подискретному признаку и непрерыным,
если – по непрерывному.
В случае непрерывного признака целесообразно строить гистограмму. На оси
Ох строятся интервалы, над которыми строятся прямоугольники с высотой, равной
частоте (относительной частоте) соответствующего интервала.
Площадь гистограммы равна сумме всех частот, т.е. объему выборки.( в случае
относительных частот = 1).
2. Эмпирическая ф-я распределения.(э.ф.р.)
Опр. Э.Ф.Р. (ф-й распределения выборки) наз ф-ю F*(х), определяющую для
каждого значения х относительную частоту события Х<х: F*(х)=nx/n,
nx –число вариант, меньших х, n- объем выборки.
3. Выборочная средняя
Опр. Выборочной средней Хв(над Х необходимо рисовать черточку) наз среднее
арифметическое значение признака выборочной совокупности. Если все значения х
1,х2,.,хn различны, то
Хв=(х1+х2+.+ хn)/n.
Если значения признака х1,х2,.,хk имеют
соответственно частоты n1,n2,.,nk, причем n
1+n2+.+nk =n, то
Хв=(∑i=1knixi)/n,
т.е. выборочная средняя есть средняя взвешанная значений признака с весами,
равными соответствующим частотам.
4. Выборочная дисперсия.
Выборочной дисперсией Dв наз среднее арифметическое квадратов отклонений
наблюдаемых значений признака от их среднего значения Хв (с чертой).
Если все значения х1,х2,.,хn различны, то
Dв=(∑i=1n(xi – xв )2)/n
Если значения признака х1,х2,.,хk имеют
соответственно частоты n1,n2,.,nk, причем n
1+n2+.+nk =n, то Dв=(∑i=1
kni(xi – xв )2)/n, т.е.
выборочная дисперсия есть средняя взвешанная квадратов отклонений с весами,
равными соответствующим частотам.
5. Статистические оценки: несмещенные, эффективные, состоятельные
Рассматривая x1, x2, . , xn как независимые случайные величины
X1, X2, . , Xn, можно сказать, что найти
статистическую оценку неизвестного параметра теоретического распределения – это
значит найти функцию от наблюдаемых случайных величин, которая и дает
приближенное значение оцениваемого параметра.
Статистической оценкой неизвестного параметра теоретического распределения
называют функцию от наблюдаемых случайных величин.
Пусть Θ* - статистическая оценка неизвестного параметра Θ
теоретического распределения.
Несмещенной называют статистическую оценку Θ*, математическое
ожидание которой равно оцениваемому параметру Θ при любом объеме выборки,
т. е.
М(Θ*) = Θ.
Возможные значения Θ* могут быть сильно рассеяны вокруг своего среднего
значения, т. е. дисперсия D (Θ*) может быть значительной Þ
существует возможность допустить большую ошибку. По этой причине к
статистической оценке предъявляется требование эффективности.
Эффективной называют статистическую оценку, которая (при заданном объеме
выборки n) имеет наименьшую возможную дисперсию.
Состоятельной называют статистическую оценку, которая при n ® ¥
стремится по вероятности к оцениваемому параметру. Например, если дисперсия
несмещенной оценки при n ® ¥ стремится к нулю, то такая оценка оказывается
и состоятельной.
6. Точность и надежность оценки
Пусть найденная по данным выборки статистическая характеристика Θ* служит
оценкой неизвестного параметра Θ. Если Δ > 0 и | Θ – Θ*|
< Δ, то чем меньше Δ, тем оценка точнее. Таким образом,
положительное число Δ характеризует точность оценки.
Надежностью (доверительной вероятностью) оценки Θ по Θ*
называют вероятность g, с которой осуществляется неравенство | Θ –
Θ*| < Δ. Обычно надежность оценки задается наперед, причем в
качестве g берут число, близкое к единице. Наиболее часто задают надежность,
равную 0,95; 0,99 и 0,999.
Доверительным называют интервал (Θ* - Δ, Θ* + Δ),
который покрывает неизвестный параметр с заданной надежностью g.
Для определения необходимой численности выборки нужно задать уровень точности
выборочной совокупности (Δ) с определенной вероятностью
(g). Ф
((Δ√n ) / σ) = g / 2 Þ можно найти значение t =
(Δ√n ) / σ Þ n = (t2σ2)/Δ
2
7. Понятие о критериях согласия. Проверка гипотез о равенстве долей и
средних. Проверка гипотезы о виде распределения.
Статичтической называют гипотезу о виде неизвестного распределения, или о
параметрах известных распределений. Нулевой (основной) называют
выдвинутую гипотезу Н0. Конкурирующей (альтернативной)
называют гипотезу Н1, которая противоречит нулевой. Правило, по
которому принимают решение о том, принять или отклонить гипотезу Н0,
называют критерием. Обычно критерием служит некая случайная величина,
вычисляемая по выборке. (Критерием согласия называют критерий проверки
гипотезы о предполагаемом законе не известного распределения.)
В итоге статистической проверки гипотезы в двух случаях может быть принято
неправильное решение, т.е. могут быть допущены ошибки двух родов: 1)ошибка
первого рода состоит в том, что будет отвергнута правильная гипотеза; 2)
ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Вероятность совершить ошибку первого рода принято обозначать через a. Её
называют уровнем значимости.
Статичтическим критерием называют величину К, которая служит для проверки
нулевой гипотезы.
Критической областью называют совокупность значений критерия, при которых
нулевую гипотезу отвергают. Облать принятия гипотезы – совокупность
значений критерия, при которых гипотезу принимают. Основной принцип
проверки статистических гипотез: если наблюдаемое значение критерия
принадлежит критической области – гипотезу отвергают, если наблюдаемое значение
критерия принадлежит области принятия гипотезы – гипотезу принимают.

облать значений К разбивается на две подоблати: подоблать принятия нулевой
гипотезы (К кр.лев; К кр.прав); подобласть отклонения гипотезы Н0.
Из определения уровня значимости следует, что a=ò К кр.лев f(k)dk+ò+¥f(k)dk
-¥ К кр.прав.
Если плотность распределения К симметрична относительно оси ординат,то
ò+¥f(k)dk=a/2. Если f(k) и a известны, то можно найти К кр.прав.
К кр.прав.
Проверка гипотезы по равенству математических ожиданий нормально
распределённых совокупностей при известных дисперсиях.
Пусть Х – нормально распределённая случайная величина с неизвестным М(х)=ах
и известной D(x)=G2x ; Y - нормально распределённая
случайная величина с неизвестным М(х)=ау и известной D(x)=G2
y
В результате проведённого эксперимента вычисляется хсредняя и усредняя.
Выдвигаем гипотезу Н0: ах=ау и конкурирующую гипотезу Н1: ах не равно ау.
Требуется оценить нулевую гипотезу с уровнем значимости a.
Решение.
Хcр. распределена по нормальному закону Þ М(х)=ах и
D(x)=G2x/n. Уср. распределена по нормальному
закону Þ М(у)=ау и D(у)=G2y/m
Хср.-Уср. распределена по нормальному закону Þ
М(х-у)=0 и D(x-у)=G2x/n+G2y/m.
Введём случайную величину К= Хср .- У ср.
Ö G2x/n+G2y/m ÞК имеет
нормальное распределение с М(к)=0 и D(k)=1. Þ нормальное распределение
симетрично Þò+¥f(k)dk=a/2=0,5-Ф(К
кр.прав.)
К кр.прав.
Далее находим по таблицам фукнции Лапласса К кр.прав. Далее находим Кнабл.
Затем: 1) Если Кнабл.Î[Ккр.лев; К кр.прав.], то гипотеза Н0
принимается. 2) если КнаблÎ{критическая область}, то гипотеза Н0
отвергается.
Проверка гипотезы о равенстве математическом ожидании нормально
распределённой случайной величины при равных неизвестных диспрерсиях.
Пусть Х – нормально распределённая случайная величина с неизвестным М(х)=ах
и D(x)=G2 ; Y - нормально распределённая случайная величина с
неизвестным М(х)=ау и D(x)=G2
В результате проведённого эксперимента вычисляется хсредняя и усредняя.
Выдвигаем гипотезу Н0: ах=ау и конкурирующую гипотезу Н1: ах не равно ау.
Требуется оценить нулевую гипотезу с уровнем значимости a.
Решение.
Построим К.
n . n .
S2x=(å(xi-x)2)/(n-1), S2y=(å(yi-y)2)/(n-1).
i=1 i=1
Х – случайная величина, распределённая по нормальному закону с числовыми
характеристиками (ах, G/Ön). Y – случайная величина,
распределённая по нормальному закону с числовыми характеристиками (аy
, G/Öm)
Оказывается случайная величина S2x и S2y
имеют распределение c2(«хи-квадрат») со степенями свободы (n-1) и
(m-1).
Введём случайную величину U=((n-1)S2x)/G2
+((m-1)S2y)/G2 имеет распределение c2
с числом степеней свободы n+m-2.
Случайная величина Х-У имеет нормальный закон распределения с характеристиками
(ах-ау, ÖG2/n+G2/m
Ø)
Поэтому нормализированная случайная величина
U = (х-у)-(ах-ау)
ÖG2/n+G2/mØ
Имеет нормальное распределение N(0,1), а отношение
V = (
x- y) –(ax-ay) .
ÖU/(m+n-2)Ø sÖ1/m+1/nØÖ[(m-1)S2x/s2+(n-1)S2y/s2]*1/(m+n-2)
имеет распределение Стьюдента с (m+n-2) степенями свободы. Таким образом
можно найти Кнабл.
Кнабл. =(х-у)/Ö(1/m+1/n)*[(m-1)S2x+(n-1)S2y]/(m+n-2)Ø
Имеет распределение Стьдента с (m+n-2) степенями своды. Далеее вывод делается
как в предыдудей задаче.
8. распределение l2
Распределение l2 – закон распределения непрерывной случайной
величины, плотность которой определяется формулой.
f l2 (x)= ì 1* e-x/2x(k/2)-1, x>0
í2k/2Г(k/2)
î0, x£0
¥
чило к=n-1 - число степеней свободы. Г(х) – гамма-функция Г(х)=ò tx-1e-tdt
0
C увеличением степеней свободы распределение медленно приближается к
нормальному. Причём для f l2 (x) М{ }=n, D{ }=n2

Для дальнейшего «въезжания» необходимо иметь хотя бы отдаленное представление
о следующих понятиях
9. Распределение Стьюдента ( или t-распределение) .
Пусть Z – нормальная случайная величина, причём M(Z)=0, s(Z)=1, а V –
независимая от Z величина, которая распределена по закону c2 с к
степенями свободы. Тогда величина Т= Z
ÖV/kØ
(отношение нормированной нормальной величины к квадратному корню из независимой
случайной величины, которая распределена по закону c2 с к степенями
свободы, делённой на к, распределено по закону Стьюдента с к степенями
свободы.)
10. Распределение F Фишера – Снедекора.
Если U и V- независимые случайные величины, распределённые по закону c2
со степенями свободы к1 и к2, то величина F=U/k1
V/k2
имеет распределение, которое называется распределением F Фишера-Снедекора со
степенями свободы к1 и к2 (иногда его обозначают через V
2)
Плотность распределения. f(x) =Г((m+n)/2)*mm/2*nn/2 * xn/2-1
Г(m/2)*Г(n/2) (m+nx)(m+n)/2, x>0
При больших m и n переходит в нормальное распределение. Число степеней свободы k
1=n-1,k2=m-1.

(cправка закончена)
11. Проверка аналитических гипотез
1. Сравнение двух средних норм генеральных совокупностей, дисперсии
коттрых известны.
2. Сравнение двух средних нормальных генеральных совокупностей, дисперсии,
которых неизвестны и одинаковы.
Дано Х и У – случайные величины с нормальными распределениями.
Найдены Хср. и Уср. Известно – G2x=G2y=G2
MX=MY при конкурирующей гипотезе. Н1: МХ не равно МУ с уровнем значимости a.
Схема решений.
1. Находим S2x и S2y - исправленные выборочные.
2. Вычисляем набд=людаемое значение критерия
Т= ( x- y) * mn(m+n-2)
(n-1)S2x+(m-1)S2Y Ö m+n
Оказывается критерий Т –случайная величина распределения Стьюдента.
3. По заданному уровню значений a и числу степеней свободы k=m+n-2 по таблице
критических точек распределения Стьюдента находим критическое значение
параметра Ткр. (a, к)
4. Сравниваетм Ткр. И Тнабл., делаем вывод:
а) если |Тнабл.|< Ткр.(a, к), то нет оснований отвергнуть Н0.
б) если |Тнабл.|>Ткр.(a, к), то гипотезу отвергаем.
3 . Сравнение двух дисперсий нормальных генеральных совокупностей.
Х и У – нормальные генеральные совокупности. По выборкам найдены S2
x и S2y Требуется проверить гипотезу Н0:
DX=DY при конкурирующей гипотезе Н1 а) DX>DY б)DX не равно DY.
Схема решение в случае а).
1. Вычисляется наблюдаемое значение критерия. Fнабл.= S2больша е
/ S2меньшая =S2x/ S2
y. Оказывается, что F – случайная величина, распределённая по закону
Фишера-Снедекора.
2.По заданному уровню значимости a и числу степеней свободы k1=n-1,k
2=m-1 находим критическую точку Fкр. (a,k1,k2) k
1 – число степеней свободы большей дисперсии,k2 - число
степеней свободы меньшей дисперсии.
3.Сравнивая Fкр. и Fнабл. ,делаем вывод: Если Fкр. < Fнабл., то гипотезу Н
0 принимаем, если Fкр. > Fнабл., то гипотезу отвергаем.
Схема решения в случае б) аналогична,только в №2 F(a/2,k1,k2
), в №3 k1=n-1,k2=m-1 или k2=n-1,k1
=m-1 , так как k1 – число степеней свободы большей дисперсии,k2
- число степеней свободы меньшей дисперсии.
Проверка статистической гипотезы о виде закона распределения (Критерий Пирсона).
Х – случайная величина. Требуется но уровню значимости a проверить гипотезу о
нормальном распределении Х.
Схема решения.
1. Весь интервал выборочных значений разделить на S частных интервалов
одинаковой длины. Находим середины частичных интервалов, переходим к новому
выборочному распрелению. ni –число фактических зачений попавших в
i интервал.
2. Для получения последовательности равностоящих вариантов находим
X* ср =(åSi=1nixi)/n, G*=Öåni*(xi-x*)2/nØ.
попадания х в i интервал. Если х – нормально распределённая случайная величина,
то Z распределена по нормальному закону с нулевым математическим ожиданием и
единичной дисперсией и pi=Ф(Zi+1) – Ф(Zi
), а Zi=(xi-x*)/G*
3. Нормируем случайную величину х, рассматриваетм величину Z=(x-x*)/G*
4. вычисляем теоретические (вычисленные в предположении нормального
распределения) частоты n¢i =n*pi ,pi
- веростность
5. В качестве проверки нулевой гипотезы применим критерий Пирсона.
c2=ås(ni-ni¢)2
i=1 ni¢
6. По таблиые критических точек распределения c2 по заданному уровню
значимости a и числу степеней свободы k=s-3 находим критическую точку c2
кр.(a,к).
7. Сравнивая c2кр. и c2набл., делаем
вывод: - если c2набл.< c2кр. ,
то гипотезу о нормальном распределении Х принимаем (с уровнем значимости a)
- если c2набл.> c2кр. , то гипотезу о нормальном распределении Х отвергаем.
(Аналогично проверяется,что гипотеза принадлежит любому другому распределению,
только в № 4 рi будет считаться в соответствии с этим
распределением.)
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
| 


