|
затем
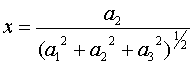 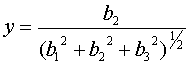
и, наконец,
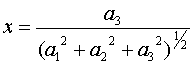 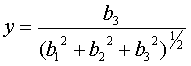
где ai, bi – действительные числа.
Складывая три полученных таким образом неравенства, имеем
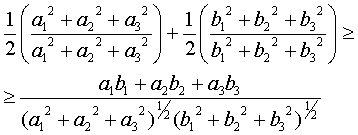 , ,
что бесспорно равносильно неравенству
(a12 + a22 + a32)½(b12 + b22 + b32)½ ³ a1b1 + a2b2 + a3b3
А это неравенство равносильно неравенству (1) при ai, bi – неотрицательных.
в) n – мерный вариант неравенства Коши будет выглядеть так
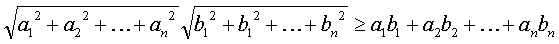
,
где ai, bi, i = 1, 2, . n – неотрицательные числа.
Неравенство Гёльдера.
Одно из наиболее полезных неравенств математического анализа – неравенство
Гёльдера. Оно утверждает, что для любой системы неотрицательных чисел ai
и bi (i – 1, 2, . , n)
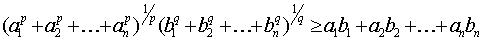
(1)
где числа р и q удовлетворяют условию
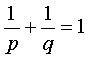 и р > 1 и р > 1
Фактически мы докажем неравенство (1) только для рациональных р и q. Однако
окончательный результат сохраняет силу и для иррациональных р и q.
Начнем с неравенства
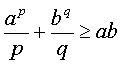 (2) (2)
Оно выводится как частный случай теоремы о среднем арифметическом среднем
геометрическом. Положим, что первые m чисел xi в неравенстве
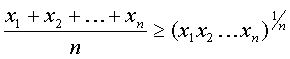
равны некоторому неотрицательному числу х, тогда остается N-m чисел и пусть
они равны неотрицательному числу у, т.е.
x1 = x2 = . = xm = x
xm+1 = xm+2 = . = xn = y
В этом случае теорема о среднем арифметическом и среднем геометрическом для
чисел x1, x2, . , xn примет вид
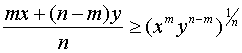
или
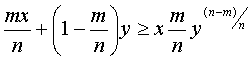
Здесь n – любое целое число, а m – целое число значения которого заключены в
пределах 1 £ m £ n – 1. Отсюда следует, что число m/n может быть
любой рациональной дробью r, принадлежащей интервалу 0 < r < 1. Теперь
последнее неравенство можно переписать так:
rx + (1 – r)y ³ x r y1-r (3)
Это неравенство имеет место для любых неотрицательных чисел х и у и для любой
дроби r, значения которой заключены между 0 и 1. Равенство здесь достигается
тогда и только тогда, когда х = у.
Обозначим число r через 1/р; поскольку 0 < r < 1, то p > 1. Отсюда
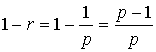 . Пусть . Пусть 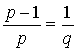 , тогда , тогда 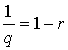 и и 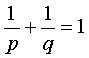
В этих обозначениях неравенство (3) принимает вид
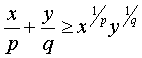 (4) (4)
С целью исключить из рассмотрения дробные показатели степени положим
х = ар, у = bр.
При этом неравенство (4) принимает вид
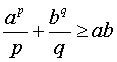 , где a и b – , где a и b –
неотрицательные числа, а р и q – такие рациональные числа, что 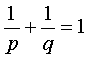
. Равенство здесь достигается тогда и только тогда, когда ар = b
р. Итак, мы вывели неравенство (2).
Положим
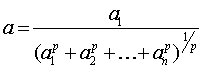 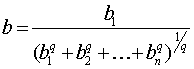
затем
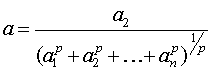 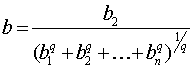
и т. д. (как в доказательстве неравенство Коши) и сложим неравенства,
получающиеся после последовательных подстановок этих значений в (2). При этом
получим
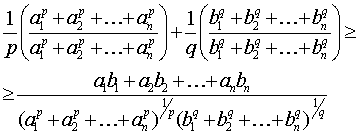 (5) (5)
Используя равенство 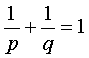
, получаем неравенство, равносильное (1). Равенство в (5) достигается тогда и
только тогда, когда все отношения bi/ai равны между
собой.
Неравенство треугольника.
Из геометрии мы знаем, что сумма длин двух сторон треугольника не меньше
длины его третьей стороны. Посмотрим, как можно выразить эту теорему
алгебраически.
Рассмотрим треугольник ORP, расположенный так, как показано на рисунке.
Геометрическое неравенство ОР + PR ³ OR равносильно алгебраическому
неравенству треугольника
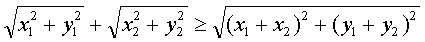
(1)
Для доказательства возведем обе части неравенства (1) в квадрат, при этом мы
придем к неравенству, равносильному (1):
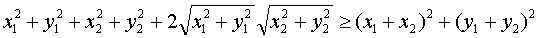
Легко видеть, что последнее неравенство в свою очередь равносильно неравенству:
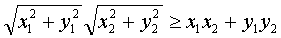
Но это неравенство является простым следствием неравенства Коши
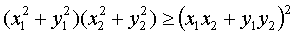 , ,
что и доказывает неравенство треугольника.
Равенство в неравенстве треугольника, как и в неравенстве Коши достигается тогда
и только тогда, когда х1 = кх2 и у1 = ку2
, где к – неотрицательный коэффициент пропорциональности.
Доказательство неравенства треугольника можно обобщить, следуя по тому же
пути, что и при выводе неравенства Гёльдера, а именно доказать, что
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31
| 


